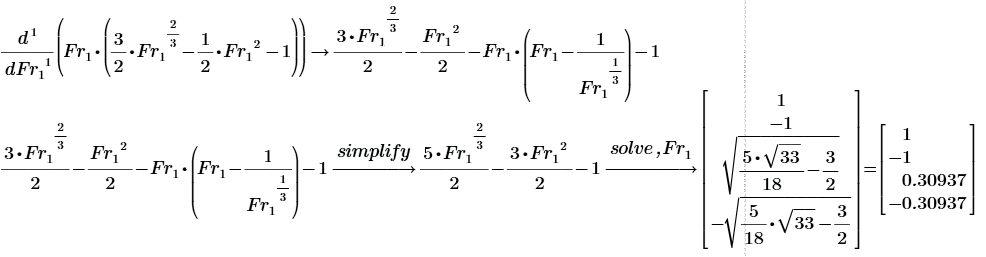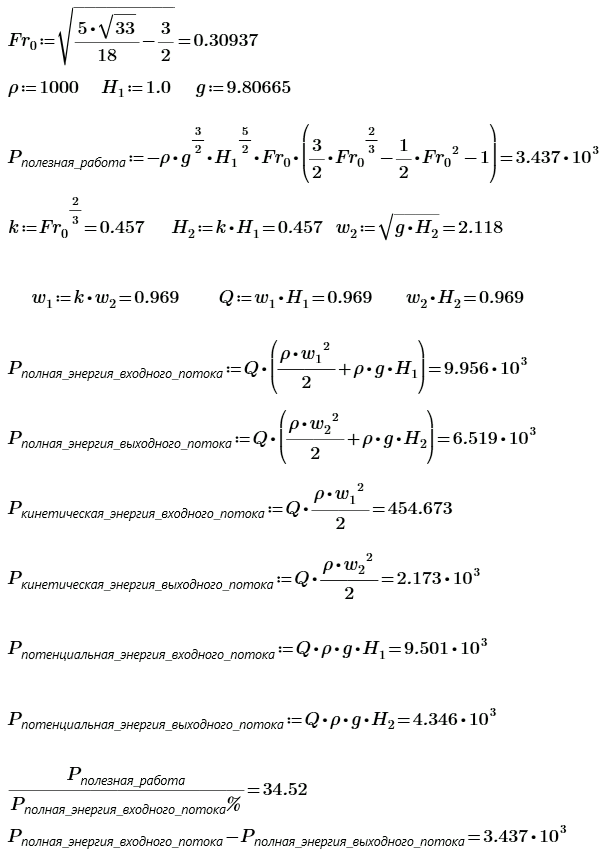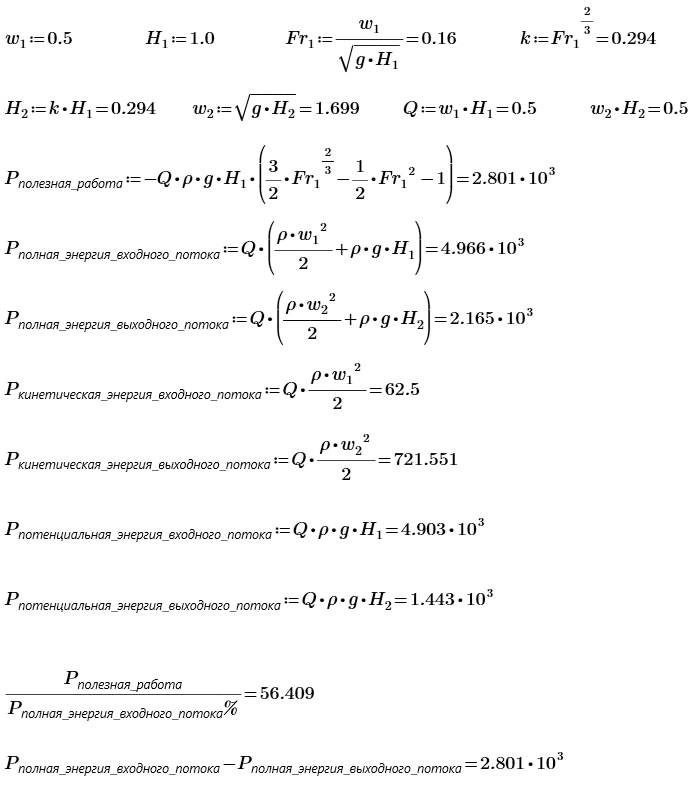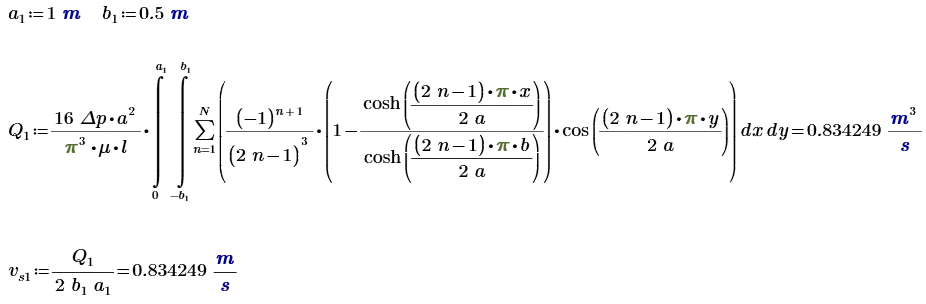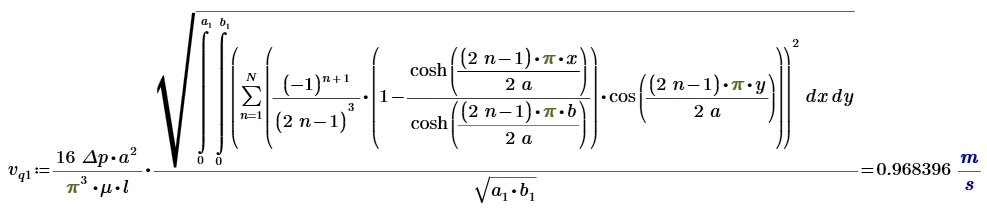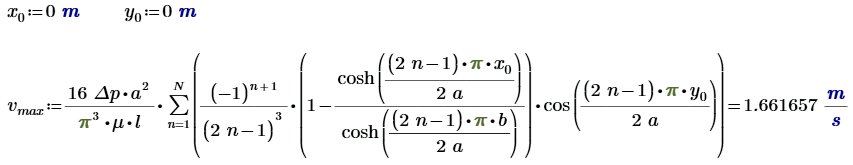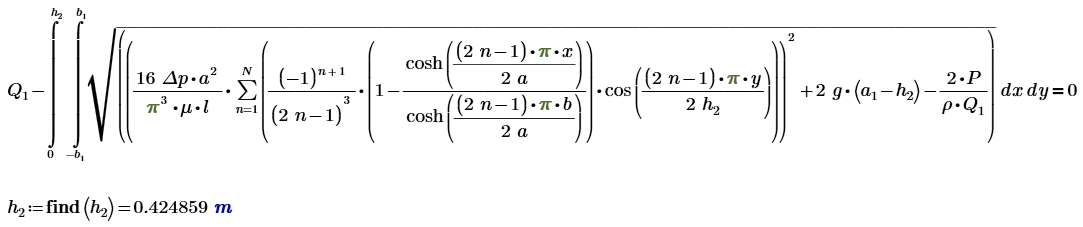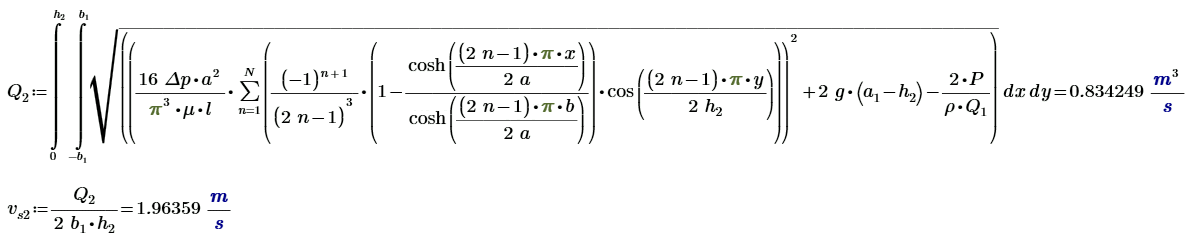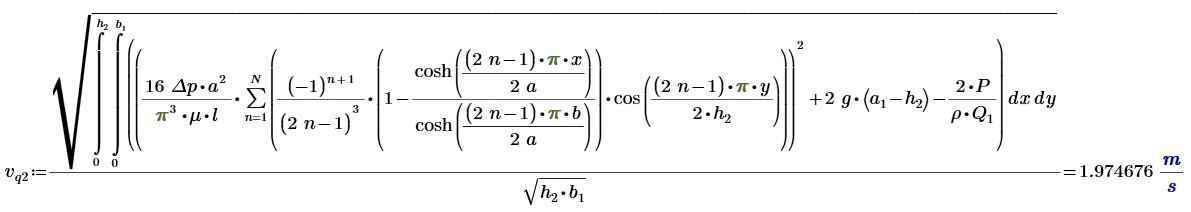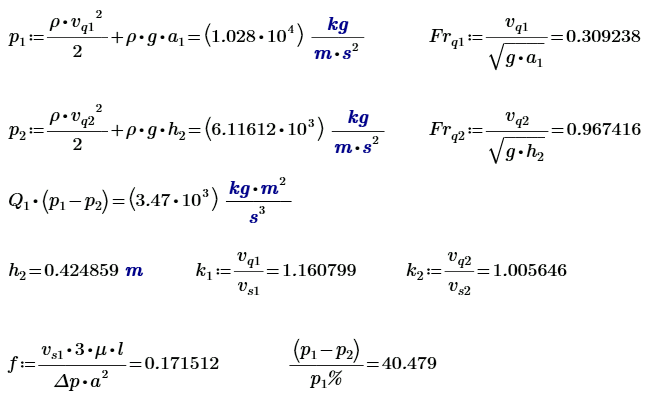|
Комментарий к публикациям Трещалова Германа Владиславовича, с изложением физического содержания в моей форме понимания. http://erg.ucoz.org/pub/info/Hydrodynamic_Effect_ru.pdf http://erg.ucoz.org/pub/info/Modelling_Effect_ru.pdf Трансформация полной энергии потока воды. Рассмотрим возможность, и особенности трансформации полной энергии потока с отбором её части в качестве полезной работы.
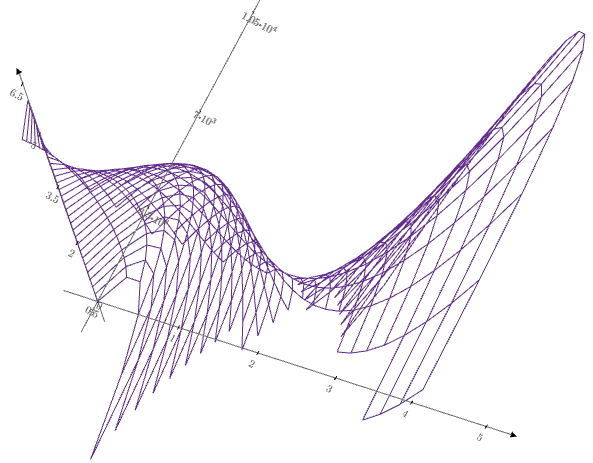
Входной поток в этой задаче приходит из математической бесконечности и после преобразования (трансформации) с другими параметрами уходит в бесконечность. Необходимость этого условия и возможность его замены другими более реальными граничными условиями, подходящими для практики, рассмотрим в дальнейшем. Подобный поток нельзя считать изолированной системой, так как для его поддержания в стационарном состоянии требуются непрерывная затрата мощности природных источников воды. Практическая реализация подобного преобразования возможна различными техническими способами, удовлетворяющими дифф. ур. \( \displaystyle ρ g \left(1 - Fr^2 \right) = \frac{de}{dH}. \) С учётом этих предположений можно записать следующее: \( \displaystyle \frac{dE_{1}}{dt} = Q \cdot \left( \frac {ρ w_{1}^2}{2} + ρ g H_{1} \right) \), где \( \displaystyle Q - \) объёмный расход воды; \( \displaystyle w_{1} - \) скорость входного потока; \( \displaystyle ρ - \) плотность воды; \( \displaystyle g - \) ускорение свободного падения. Выходного потока \( \displaystyle \frac{dE_{2}}{dt} = Q \cdot \left( \frac {ρ w_{2}^2}{2} + ρ g H_{2} \right) \), где \( \displaystyle w_{2} - \) скорость выходного потока. Проходная мощность равна \( \displaystyle \frac{d \Delta E}{dt} = -Q \cdot \left(\frac {ρ w_{2}^2}{2} + ρ g H_{2} - \frac {ρ w_{1}^2}{2} - ρ g H_{1} \right) = -Q \Delta p \). (1), где \( \displaystyle \Delta p - \) изменение давления между рассматриваемыми сечениями потока. Это изменение давления связано с потерями энергии на трение и совершение полезной работы в канале турбины. Запишем условие неразрывности потока \( \displaystyle L \cdot H_{1} \cdot w_{1} = L \cdot H_{2} \cdot w_{2} \), где \( \displaystyle L - \) ширина потока. или \( \displaystyle k = \frac{H_{2}}{H_{1} } = \frac{w_{1}}{w_{2}};~~~ \) \( \displaystyle k \cdot H_{1} = H_{2};~~~ \) \( \displaystyle \frac{w_{1}}{k} = w_{2} \). Из уравнения (1), исключаем \( \displaystyle H_{2} \). \( \displaystyle \frac{d \Delta E}{dt} = -Q \cdot \left(\frac {ρ w_{2}^2}{2} + ρ g H_{1} \frac{w_{1}}{w_{2}} - \frac {ρ w_{1}^2}{2} - ρ g H_{1} \right) = -ρ Q \cdot \left(\frac { w_{2}^2}{2} + g H_{1} \frac{w_{1}}{w_{2}} - \frac { w_{1}^2}{2} - g H_{1} \right) = \) \( \displaystyle = -ρ Q \cdot \left(\frac { w_{2}^2}{2} - \frac { w_{1}^2}{2} + g H_{1} \left(\frac{w_{1}}{w_{2}} - 1 \right) \right) = -ρ L \cdot H_{1} \cdot w_{1} \cdot \left(\frac { w_{2}^2}{2} - \frac { w_{1}^2}{2} + g H_{1} \left(\frac{w_{1}}{w_{2}} - 1 \right) \right) \). (2) Рассмотрим это уравнение в координатах \( \displaystyle (w_{1},~ w_{2}) \), при \( \displaystyle L = H_{1} = 1 м;~~~ ρ = 1000 \frac{кг}{м^3};~~~ g = 9.80665 \frac{м}{с^2} \).
Из 3D графика видно, что в области малых входных скоростей потока имеется максимум мощности. Вычислим этот максимум. Запишем (1) через k. \( \displaystyle \frac{d \Delta E}{dt} = -Q \cdot \left(\frac {ρ w_{1}^2}{2 k^2} + ρ g k H_{1} - \frac {ρ w_{1}^2}{2} - ρ g H_{1} \right) \); \( \displaystyle \frac{d \Delta E}{dt} = -Q \cdot \left(\frac {ρ w_{1}^2}{2} \left( \frac{1}{k^2} - 1 \right) + ρ g H_{1} \left( k - 1 \right) \right) \). (3) Оптимизируем по максимуму мощности в зависимости от \( \displaystyle k = \frac{H_{2}}{H_{1} }. \) \( \displaystyle \frac {d}{ d k} \left(\frac {ρ w_{1}^2}{2} \left( \frac{1}{k^2} - 1 \right) + ρ g H_{1} \left( k - 1 \right) \right) \) = 0. \( \displaystyle -\frac {ρ w_{1}^2}{2} \frac{2}{k^3} + ρ g H_{1} \) = 0. \( \displaystyle -\frac {ρ w_{1}^2}{k^3} + ρ g H_{1} = 0;~~~~ \) \( \displaystyle -\frac { w_{1}^2}{k^3} + g H_{1} \) = 0. \( \displaystyle \frac { w_{1}^2}{k^3} = g H_{1};~~~~ \) \( \displaystyle k^3 = \frac{ w_{1}^2}{g H_{1}} = \frac{ k^2 \cdot w_{2}^2 \cdot k}{g H_{2}} \). \( \displaystyle \frac{ w_{2}^2 }{g H_{2}} = 1\). \( \displaystyle w_{1}^2 = g H_{1} \cdot k^3 \). (4) Подставляем в (3) \( \displaystyle \frac{d \Delta E}{dt} = -Q \cdot \left(\frac {ρ g H_{1} k^3}{2} \left( \frac{1}{k^2} - 1 \right) + ρ g H_{1} \left( k - 1 \right) \right) = -Q \cdot ρ g H_{1} \left(\frac {k^3}{2} \left( \frac{1}{k^2} - 1 \right) + k - 1 \right) = -Q \cdot ρ g H_{1} \left( \frac {1}{2} k - \frac {1}{2} k^3 + k - 1 \right) \); \( \displaystyle \frac{d \Delta E}{dt} = -Q \cdot ρ g H_{1} \left( \frac {3}{2} k - \frac {1}{2} k^3 - 1 \right) \). (5) Число Фруда для входного потока \( \displaystyle \frac{ w_{1} }{ \sqrt{g H_{1}}} = Fr_{_1} = k^{\frac{3}{2} };~~~ \) \( \displaystyle Fr_{_1}^2 = k^3;~~~ \) \( \displaystyle Fr_{_1}^{\frac{2}{3}} = k \). Число Фруда для выходного потока всегда будет единица. \( \displaystyle \frac{ w_{2} }{ \sqrt{g H_{2}}} = Fr_{_2} = 1 \). Выразим мощность через число Фруда входного потока \( \displaystyle \frac{d \Delta E}{dt} = -Q \cdot ρ g H_{1} \left( \frac {3}{2} Fr_{_1}^{\frac{2}{3}} - \frac {1}{2} Fr_{_1}^2 - 1 \right) = -w_{1} H_{1} \cdot ρ g H_{1} \left( \frac {3}{2} Fr_{_1}^{\frac{2}{3}} - \frac {1}{2} Fr_{_1}^2 - 1 \right) = -\sqrt{g H_{1}} \cdot Fr_{_1} \cdot ρ g H_{1}^2 \left( \frac {3}{2} Fr_{_1}^{\frac{2}{3}} - \frac {1}{2} Fr_{_1}^2 - 1 \right) \) \( \displaystyle \frac{d \Delta E}{dt} = - ρ \cdot g^{\frac{3}{2}} H_{1}^{\frac{5}{2}} \cdot Fr_{_1} \cdot \left( \frac {3}{2} Fr_{_1}^{\frac{2}{3}} - \frac {1}{2} Fr_{_1}^2 - 1 \right) \) (6)
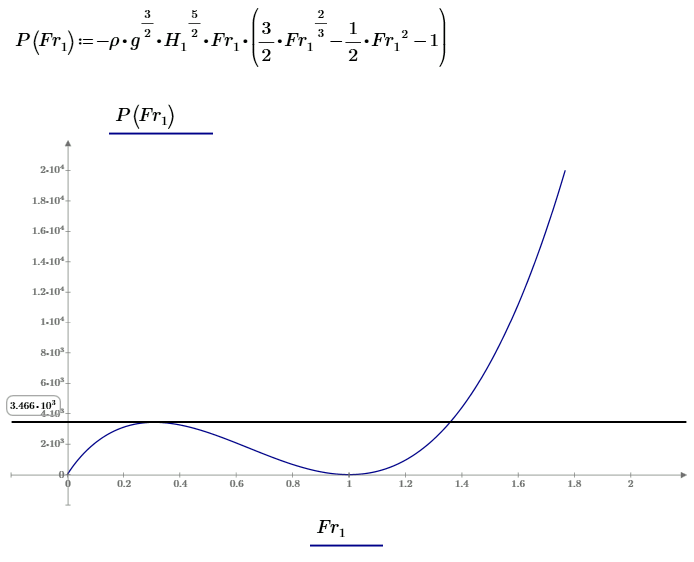
Обратите внимание, что график на Рис. 3 является сечением 3D графика Рис. 2 в максимуме мощности потока. Из графика Рис. 3 уравнения (6) видно, что положительную мощность можно получить при любых числах Фруда на входе, кроме двух случаев: 1. \( \displaystyle Fr_{_1} = 1 \), когда \( \displaystyle \frac{d \Delta E}{dt} = 0 \); \( \displaystyle H_{1} = H_{2} \); \( \displaystyle Fr_{_2} = 1 \). 2. \( \displaystyle Fr_{_1} = 0 \), потока нет.
Для \( \displaystyle \frac{d \Delta E}{dt} > 0 \) можно записать. При \( \displaystyle Fr_{_1} < 1 \) будет \( \displaystyle H_{1} > H_{2} \); \( \displaystyle Fr_{_2} = 1 \). В этой области существует максимум мощности. Вычислим число Фруда в этом максимуме. \( \displaystyle \frac{d}{d~Fr_{_1}} \left( Fr_{_1} \left( \frac {3}{2} Fr_{_1}^{\frac{2}{3}} - \frac {1}{2} Fr_{_1}^2 - 1 \right) \right) = 0 \).
Этому максимуму соответствует число Фруда \( \displaystyle \sqrt{\frac{5 \sqrt{33}}{18} - \frac{3}{2} } = 0.30937 \) В этом случае энергии выходного потока уже не хватит для подъёма воды на уровень \( \displaystyle H_{1} \). Числовой пример, для случая \( \displaystyle Fr = 0.30937 \).
При \( \displaystyle Fr_{_1} > 1 \) будет \( \displaystyle H_{1} < H_{2} \); \( \displaystyle Fr_{_2} = 1 \). Рассмотрим дополнительно числовые примеры для разных потоков При \( \displaystyle Fr_{_1} > 1 \)
При \( \displaystyle Fr_{_1} < 1 \)
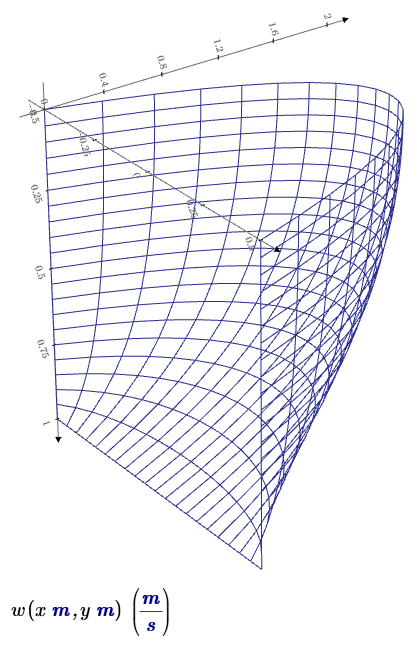
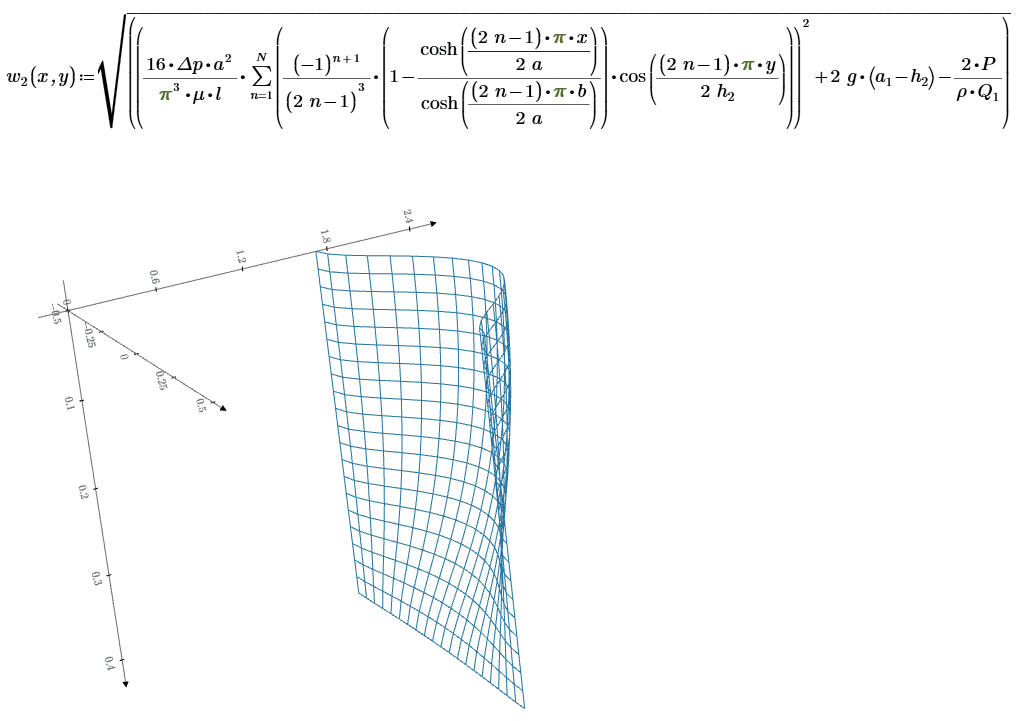
Стационарное течение потока в прямоугольном канале. Перепад высоты необходимый для его поддержания. Если рассматривать трубу прямоугольного сечения со сторонами \( \displaystyle 2a \) и \( \displaystyle 2b \) и задать форму сечения в плоскости \( \displaystyle xy \) уравнениями \( \displaystyle y = ±a \) и \( \displaystyle x = ±b \), то профиль скоростей можно вычислить по формуле: \( \displaystyle w = \frac{16 \Delta p~ a^2}{π^3 μ~ l} \sum_{n=1}^∞ \frac{(-1)^{n+1} }{(2n - 1)^3} \left[1 - \frac{ch \frac{(2n - 1) π x}{2a}}{ch \frac{(2n - 1) π b}{2a}} \right] cos \frac{(2n - 1) π y}{2a} \). И. Л. Повх. Техническая гидромеханика ст. 252. Эту формулу можно применить и для открытого прямоугольного канала выбором сечения по уравнениям \( \displaystyle y = a \) и \( \displaystyle x = ±b \). В этом случае \( \displaystyle a - \) глубина потока; \( \displaystyle 2b - \) ширина потока; \( \displaystyle \Delta p - \) перепад давления на участке длиной \( \displaystyle l \); \( \displaystyle μ - \) динамическая вязкость. Рассмотрим подробнее на числовом примере.
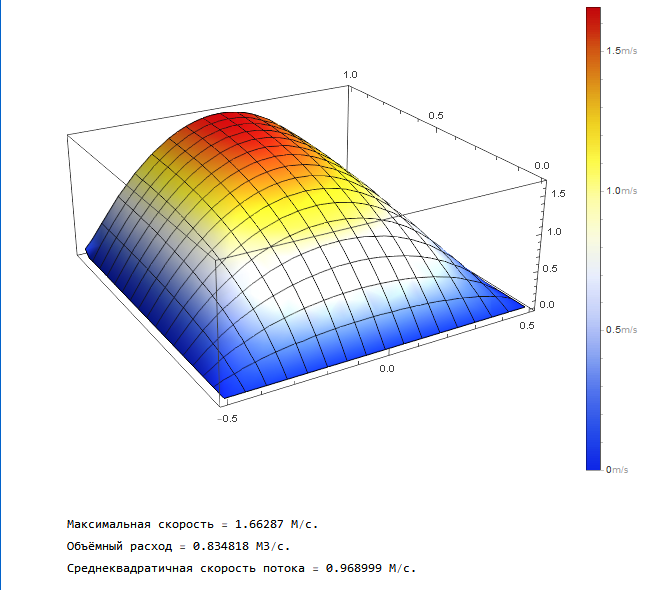
Профиль скоростей стационарного потока
Объёмный расход и средняя скорость потока
Среднеквадратичная скорость потока
Максимальная скорость потока
Параметры неустановившегося потока после турбины. Проходная мощность \( \displaystyle P = \) 3470 W. Решаем уравнение баланса расхода между сечениями относительно \( \displaystyle h_2 \)
Где \( \displaystyle h_2 - \) глубина потока на выходе турбины. Объёмный расход и средняя скорость выходного потока
Среднеквадратичная скорость выходного потока
Дополнительные параметры и проверка расчёта
Профиль скоростей неустановившегося потока на выходе
Расчёт профиля установившегося потока через дифф. ур. Лапласа. 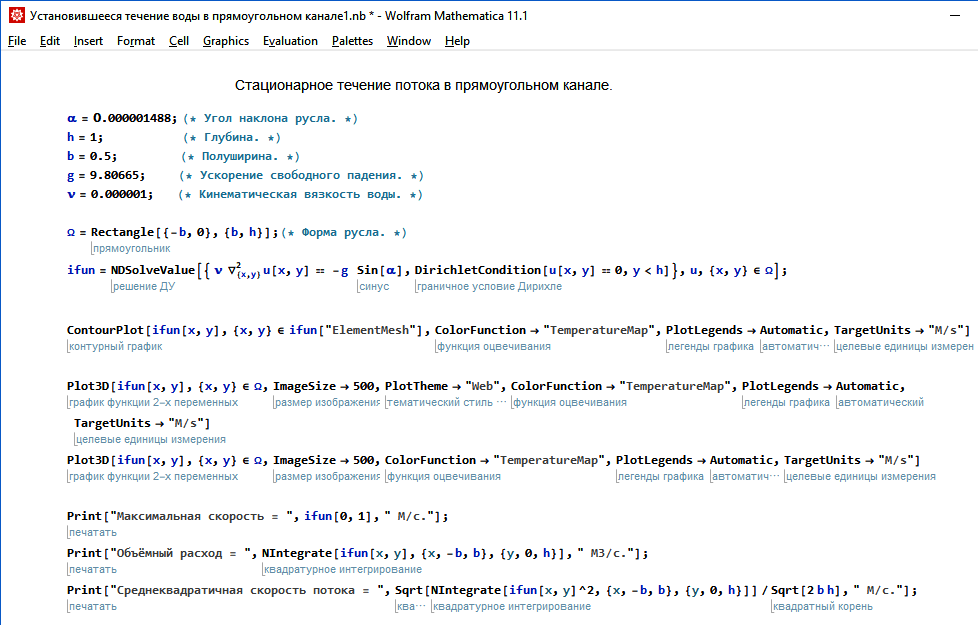
...
О теореме Бернулли.
И. Л. Повх. Техническая гидромеханика 2-е изд., доп. Л., "Машиностроение" (Ленингр. отд-ние), 1976. 504 с.
Приложение 1. Задача №1
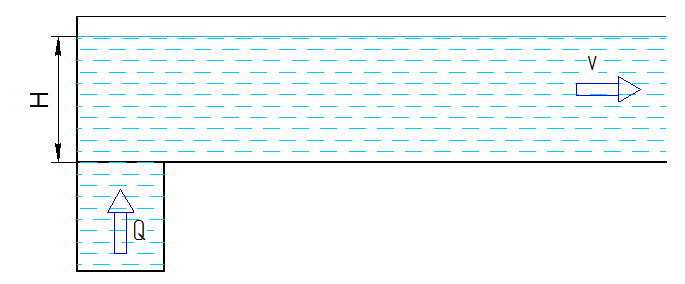
Рис. 4 Имеется открытый горизонтальный канал, рис. 4. В него через отверстие у дна, подаётся вода. Забор воды насосом производится на уровне дна канала. Объёмный расход воды равен \( \displaystyle Q \). Сечение канала \( \displaystyle L \cdot H \). Какая мощность насоса требуется для поддержания такого потока без учёта потерь на трение и турбулентность? На преодоление гидростатического давления потребуется мощность \( \displaystyle Q \cdot p\), где \( \displaystyle p = ρ g H - \) гидростатическое давление на дне. На поддержание кинетической энергии потока при скорости \( \displaystyle \frac{Q}{L \cdot H} = V \) потребуется мощность равная \( \displaystyle Q \frac{ρV^2}{2} \). В сумме \( \displaystyle Q \left( \frac{ρV^2}{2} + ρ g H \right) \). По закону сохранения энергии при сливе этого потока вода будет иметь на уровне дна именно эту кинетическую мощность.
Вычисление удельной энергии открытого стационарного потока воды в прямоугольном канале интегрированием уравнения Бернулли по поперечному сечению потока. Линия тока имеет три составляющие удельной энергии. 1. Кинетическую. Скоростной (динамический) напор. 2. Потенциальную. Геометрический напор. 3. Давление. Пьезометрический напор. \( \displaystyle \frac{dE}{dV} = \frac{ρw^2}{2} + ρ g h + p \). Первое слагаемое является кинетической энергией, второе \( \displaystyle - \) потенциальной и третье характеризует работу сил давления. Потенциальная энергия линии тока, если её измерять относительно дна канала, линейно меняется от 0 на дне до \( \displaystyle ρ g H \) на поверхности. Давление меняется наоборот от \( \displaystyle ρ g H \) на дне до 0 на поверхности. Атмосферное давление вдоль канала постоянное и его не учитываем. Других давлений в этом стационарном потоке нет. Интегрируем по высоте, ширина постоянная равная \( \displaystyle L \). \( \displaystyle L \int\limits_0^H \frac{dE}{dV} dh = L \int\limits_0^H \frac{ρw^2}{2} dh + L \int\limits_0^H ρ g h~ dh + L \int\limits_0^H p~ dh \). Давление равно \( \displaystyle p = ρ g (H - h) \). \( \displaystyle L \int\limits_0^H \frac{dE}{dV} dh = L \int\limits_0^H \frac{ρw^2}{2} dh + L \int\limits_0^H ρ g h~ dh + L \int\limits_0^H ρ g (H - h)~ dh \). \( \displaystyle L \int\limits_0^H \frac{dE}{dV} dh = L \int\limits_0^H \frac{ρw^2}{2} dh + ρ g L \int\limits_0^H h~ dh + ρ g L \int\limits_0^H (H - h)~ dh \). \( \displaystyle L \int\limits_0^H \frac{dE}{dV} dh = L \int\limits_0^H \frac{ρw^2}{2} dh + \frac{1}{2} ρ g L H^2 + ρ g L (H^2 - \frac{1}{2} H^2) \). \( \displaystyle L \int\limits_0^H \frac{dE}{dV} dh = L \int\limits_0^H \frac{ρw^2}{2} dh + ρ g L H^2 \). Находим среднее делением на площадь сечения \( \displaystyle L \cdot H \). \( \displaystyle \frac{dE_{q}}{dV} = \frac{ρw_{q}^2}{2} + ρ g H \), где \( \displaystyle w_{q} - \) среднеквадратичная скорость потока в сечении. Обратите внимание, что запись вида \( \displaystyle \frac{dE_{q}}{dV} = \frac{ρw_{q}^2}{2} + \frac{ ρ g H}{2} \), появляется только в случае пренебрежения работой давления и она не соответствует опыту. Давление совершает работу при изменении высоты слоя вдоль течения при постоянном уровне дна.
Рассмотрим следующий мысленный эксперимент. Пусть в большом водоёме подъёмное устройство извлекает воду в кубической ёмкости объёмом \( \displaystyle 1 м^3 \) и ставит её на конвейер, движущийся со скоростью V. Конвейер находится на уровне воды. Процесс извлечения непрерывный, между кубами на конвейере нет расстояний (монолит). Удельная энергия этого процесса \( \displaystyle \frac{dE}{dV} = \frac{ρV^2}{2} + \frac{ ρ g H}{2} \). При падении куба обратно в воду он будет иметь именно эту кинетическую энергию, без учёта потерь. Для сторонников применения к потоку формулы \( \displaystyle \frac{dE}{dV} = \frac{ρV^2}{2} + \frac{ ρ g H}{2} \), приведённые рассуждения являются доказательством их правоты. Однако в реальности между кубами нет перегородок и, если мы откроем один конец такого канала на слив, то на противоположную сторону канала будет действовать не скомпенсированное среднее давление равное \( \displaystyle \frac {ρ g H}{2} \). Пока поддерживается поток, это давление будет постоянно, и конвейер по этой причине будет совершать дополнительную работу. Удельная энергия этого процесса будет равна \( \displaystyle \frac{dE}{dV} = \frac{ρV^2}{2} + \frac{ ρ g H}{2} + \frac{ ρ g H}{2} = \frac{ρV^2}{2} + ρ g H \). Это удельная энергия, которая требуется на создание потока (задача №1). При сливе потока кинетическая мощность на уровне водоёма будет именно такая. Многие забывают, что при создании потока необходимо дополнительно совершать работу по проталкиванию каждого нового объёма по течению, преодолевая среднее давление в сечении потока равное \( \displaystyle \frac {ρ g H}{2} \). Чтобы создать поток необходимо совершить удельную работу по подъёму воды равную \( \displaystyle \frac{ ρ g H}{2} \) и удельную работу по проталкиванию этого объёма по течению тоже равную \( \displaystyle \frac{ ρ g H}{2} \). Или можно воду сразу поднять по трубе на высоту \( \displaystyle H \), что соответствует удельной энергии \( \displaystyle ρ g H \). Или закачать воду под слой с давлением \( \displaystyle ρ g H \), что соответствует удельной энергии \( \displaystyle ρ g H \).
Формула \( \displaystyle \frac{dE}{dV} = \frac{ρV^2}{2} + \frac{ ρ g H}{2} \) применима только для потока сыпучих материалов. Поздравляю сторонников формулы \( \displaystyle \frac{dE}{dV} = \frac{ρV^2}{2} + \frac{ ρ g H}{2} \) для потока воды, с изобретением первого в мире абсолютного уничтожителя энергии. Это гидродинамическая машина поглощает энергию без выделения тепла, что является не малым экологическим достижением. На входе \( \displaystyle \frac{ρV^2}{2} + ρ g H \). На выходе \( \displaystyle \frac{ρV^2}{2} + \frac{ ρ g H}{2} \).
Приложение 2.
Гидравлика и гидравлические машины 1 Гидравлика и гидравлические машины 2 Гидравлика и гидравлические машины 3
Михаил Ost. Редакция от 23.07.2013 г. Продолжение следует. Вопросы можно задавать на форуме Трансформация полной энергии потока воды. Оглавление сайта
|
||

Механика инерцоида
| ||
| Главная | Трансформация полной энергии потока | Мой профиль | Выход | Вы вошли как Гость | Группа " Гости" | RSS |  |