На этой странице будет производиться анализ статьи «Влияние трения на движение инерцоида» из межвузовского сборника научных трудов за 1996 г.
Автор научной статьи – Тарунин Евгений Леонидович, доктор физико-математических наук, профессор Пермского государственного университета.

Статья цитируется с моими комментариями. Комментарии печатаются на зелёном фоне. В цитаты вошёл только материал, имеющий информационное значение или связан с анализом. Некоторые обозначения и стиль текста изменены для удобства ввода. Введены дополнения для более полного понимания математических выкладок. Цель анализа – показать, что использованные в работе числовые параметры, для программного моделирования виброхода, только доказывают, что реальное движение инерцоида не соответствует классической механике. Анализ будет состоять из двух частей. В первой части комментарии сопровождают текст статьи. Её задача выделить противоречия, интересные и проблемные места, определится с параметрами, которые надо использовать в модели, соответствующей опыту. Во второй части мы проведём программный анализ модели Евгения Леонидовича в более широком виде, при обоснованных экспериментом параметрах и без оптимизации Автора.

Михаил Ost
г. Пермь

Часть 1

Редакция от 21.08.2011 г.

ПРОБЛЕМЫ МЕХАНИКИ И УПРАВЛЕНИЯ
Нелинейные динамические системы
Межвузовский сборник научных трудов. 1996

УДК 531.314.2+519.62

Е. Л. Тарунин
г. Пермь
Влияние трения на движение инерцоида

...
Инерцоид представляет для механики яркий пример механизма, который чутко реагирует на зависимость трения от скорости. В работе исследовано движение инерцоидов как механизмов, которое полностью подчинено законам классической механики. ...

Цель данной статьи — показать ещё раз (как это было сделано в [9] ), что движение инерцоида правильно описывается законами классической механики. ...

     1. Сведения об инерцоидах [3]. Опишем кратко основные характеристики инерцоидов и укажем параметры, которые могут быть использованы при расчётах. Инерцоид обычно располагался на тележке, опирающейся на 4 колесика. На тележке располагался и электродвигатель (в первых конструкциях пружинный механизм). Электродвигатель вращает вертикальный вал, на котором синхронно, но в различных направлениях вращаются в горизонтальных плоскостях два рычага с грузиками на концах (один рычаг вращается по часовой стрелке, а другой — против). Двигатель включался периодически кратковременно для разгона грузиков в основном в поперечном направлении по отношению к оси инерцоида (рис.1).

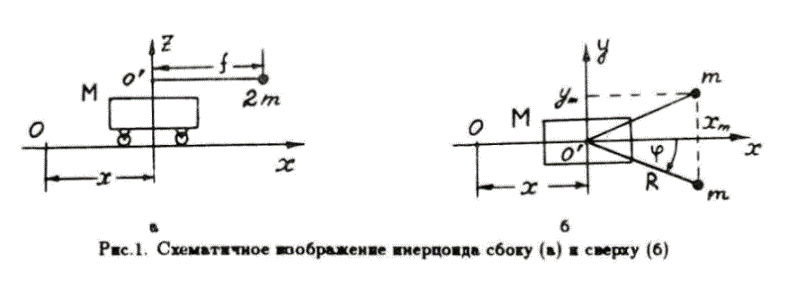
     Плоскости вращении грузиков были немного разнесены по высоте. Радиусы грузиков могут быть различными (по фото однотактного инерцоида с электроприводом различие в радиусах составляет около 20%). В математической модели отражены только две основные части инерцоида — корпус тележки и два рычага, расположенные симметрично относительно оси движения и оси инерцоида. В [3] отмечено, что "особое внимание необходимо уделять тормозному механизму, именно он регулирует верный режим работы инерцоида". Безусловно, это так (у Толчина В.Н. тонкое чутье механика-изобретателя), но, к сожалению, описание тормозного механизма [3] сводится лишь к формальной стороне (размеры, материал, способ крепления) без указания функциональных параметров. Сектора ускорения и замедления (торможения) грузиков были таковы:

φ₁ = 160° ≤ φ < φ₂ = 180° – сектор торможения,

φ₃ = 330° ≤ φ < φ₄ = 360° – сектор ускорения.

(1.1)

     Эти сектора указаны в предположении, что угол φ (см. рис. 1,б) отсчитывается от оси x и значение φ = 0 соответствует нахождению грузиков впереди корпуса. Отметим, что указанное значение сектора торможения Δφ₂ = 20° находится в противоречии с углом тормозного кулачка (рис. 26 [3]), равным 35°.
     Из математической модели будет видно, что важной характеристикой устройства является безразмерная величина, равная отношению массы грузиков к полной массе

\(\displaystyle γ=\frac{2m}{M_0}\).

По данным табл. 1 эта величина изменялась от 0.274 до 0.46.

Таблица 1

     Другой важной характеристикой устройства является масштаб длины

\(S_0 =2 γ R\).

(1.3)

Эта величина определяет амплитуду колебаний механического вибратора при отсутствии трения. По данным [3], эта величина меньше хода вперёд S₊ в 2–2.7 раза.
     Период обращения грузиков изменялся в довольно широких пределах – 0.2 ÷ 0.3 до 1–2 с (табличные данные по каждому типу устройства отсутствуют). ...

При изменении настройки "пружинного" инерцоида с 1.0 до 0.3 сек, уровень центростремительных сил увеличивается в 11.11 раза, а средние силы сухого трения уменьшаются, так как, по мнению некоторых оппонентов инерцоид работает на спаде характеристики трения в зависимости от скорости. Однако факт, что это не приводит к существенным изменениям в параметрах движения, 90/30. Поэтому сторонники В. Н. Толчина задают вполне справедливый вопрос, а причём тогда здесь трение? Чувствительность параметров инерцоида к отношению (трение)/(центростремительная сила) весьма незначительна в заметном дипазоне частот, по факту реального опыта, при условии минимизации трения элементарно доступными способами, т. е. использования качественного колеса с большим отношением его диаметра к диаметру оси, в условиях смазки. Всякие разговоры о большом и нелинейном трении, двигающим инерцоиды, не имеет под собой никакой практической основы. Они является просто теоретическими вымыслами, которые стимулируются отсутствием других вариантов классического объяснения причин движения инерцоидов.

     3. Вывод уравнений Лагранжа и решение уравнений механического вибратора. Осуществим вывод уравнений, определяющих движение системы двух тел – корпуса тележки и вращающихся грузиков. Система координат изображена на рис. 1,б. Полная кинетическая энергия системы (лагранжиан) равна

\(\displaystyle L=\frac{M v^2}{2}+\frac{2m(v_{xm}^2+v_{ym}^2)}{2}\);

(3.1)

здесь M – масса тележки, 2m – масса вращающихся грузиков. Между координатами оси тележки x и координатами грузиков x_m и y_m имеется жесткая кинематическая связь.

\(\displaystyle x_m=x+Rcos(φ),~~~~~~~y_m= ± Rsin(φ)\).

(3.2)

Дифференцирование уравнения (3.2) по времени и подстановка в (3.1) даёт для кинетической энергии выражение

\(\displaystyle L=\frac{M_0~v^2}{2}+m(ω^2 R^2-2R~v~ ω \cdot sin(φ))\).

(3.3)

\(\displaystyle v_{xm}=v-ω R sin(φ)~~~~~v_{ym}=±ωRcos(φ)\).

\(\displaystyle L=\frac{Mv^2}{2}+\frac{2m((v-ω R sin(φ))^2+(ωRcos(φ))^2)}{2}=\)

\(\displaystyle =\frac{Mv^2}{2}+m(v^2+ω^2 R^2 sin(φ)^2 - 2v~ ω R sin(φ)+ω^2 R^2 cos(φ)^2)=\)

\(\displaystyle =\frac{Mv^2}{2}+m(v^2+ ω^2 R^2-2v~ ω~R \cdot sin(φ))\).

\(\displaystyle L=\frac{M_0~v^2}{2}+m(ω^2 R^2-2R~v~ ω \cdot sin(φ))\).

Здесь \(\displaystyle M_0=M+2m~-\) полная масса инерцоида, \(\displaystyle v=\frac{dx}{dt}~-\) скорость тележки, \(\displaystyle ω=\frac{d φ}{dt}~-\) угловая скорость рычагов радиуса R.
     Уравнение Лагранжа, определяющие динамику системы, имеют вид [16]

\(\displaystyle \frac{d}{dt}\left(\frac{∂L}{∂q'_{i}}\right)-\frac{∂L}{∂q_i}=Ψ_i\)

(3.4)

в котором q_i – обобщённые координаты, а Ψ_i – обобщённые силы. В нашем случае для двух обобщённых координат (i = 1,2)

q₁ = x,    q₂ = φ

(3.5)

уравнения Лагранжа (3.4) приобретают вид

\(\displaystyle \frac{dv}{dt}=γR\left(cos(φ)\left(\frac{dφ}{dt}\right)^2+sin(φ)\frac{dω}{dt}\right)+\frac{Ψ_x}{M_0}\)

(3.6)

\(\displaystyle L=\frac{M_0~v^2}{2}+mω^2 R^2- 2mR~v~ω~sin(φ)\);

\(\displaystyle \frac{∂L}{∂v}=M_0~v-2mRω~sin(φ)\);

\(\displaystyle \frac{d}{dt}\left(\frac{∂L}{∂v}\right)=M_0\frac{dv}{dt}-2mR\frac{dω}{dt} sin(φ)-2mRω^2~cos(φ)\);

\(\displaystyle \frac{∂L}{∂x}=0\);

\(\displaystyle \frac{d}{dt}\left(\frac{∂L}{∂v}\right)-\frac{∂L}{∂x}=M_0\frac{dv}{dt}-2mR\frac{dω}{dt} sin(φ)-2mRω^2~cos(φ)=Ψ_x\);

\(\displaystyle M_0\frac{dv}{dt}=2mRω^2~cos(φ)+2mR\frac{dω}{dt}sin(φ)+Ψ_x\);

\(\displaystyle \frac{dv}{dt}=γR ω^2~cos(φ)+γR\frac{dω}{dt} sin(φ)+\frac{Ψ_x}{M_0}\);

\(\displaystyle \frac{dv}{dt}=γR\left(ω^2 ~cos(φ)+\frac{dω}{dt} sin(φ)\right)+\frac{Ψ_x}{M_0}\).

\(\displaystyle \frac{dω}{dt}=\frac{sin(φ)}{R} \frac{dv}{dt}+\frac{Ψ_φ}{I}\).

(3.7)

\(\displaystyle L=\frac{M_0~v^2}{2}+mω^2 R^2- 2mR~v~ω~sin(φ)\);

\(\displaystyle \frac{∂L}{∂ω}=2mωR^2-2mR~v~sin(φ)\);

\(\displaystyle \frac{∂L}{∂φ}=-2m~v~ωRcos(φ)\);

\(\displaystyle \frac{d}{dt}\left(\frac{∂L}{∂ω}\right)=2m\frac{dω}{dt}R^2-2mR\frac{dv}{dt}sin(φ)-2mR~v~ω~cos(φ)\);

\(\displaystyle \frac{d}{dt}\left(\frac{∂L}{∂ω}\right)-\frac{∂L}{∂φ}=2m\frac{dω}{dt}R^2-2mR\frac{dv}{dt}sin(φ)=Ψ_φ\);

\(\displaystyle \frac{dω}{dt}-\frac{dv}{dt} \frac{sin(φ)}{R}=\frac{Ψ_φ}{I}\);

\(\displaystyle \frac{dω}{dt}=\frac{dv}{dt} \frac{sin(φ)}{R}+\frac{Ψ_φ}{I}\).

Здесь Ψ_x(v) – сила сопротивления движению корпуса тележки (внешняя сила), Ψ_φ – момент сил, вращающий грузики, \(\displaystyle γ=\frac{2m}{M_0}\),     I = 2mR² – момент инерции грузиков.
    Из формулы для координат центра масс x_c (2.3) и связей (2.2) вытекают соотношения:

v_c = v - γ·R·sin(φ)·ω,

dv_c/dt = dv/dt - γ·R·(cos(φ)·ω² + sin(φ)·dω/dt).

(3.8)

Отсюда и (3.6) следует, что при отсутствии внешней силы (Ψ_x = 0) ускорение центра масс тождественно равно нулю, или, что то же, – скорость движения центра масс dx_c/dt = const. ...

     4. Решение уравнений Лагранжа.
     Для удобства реализации пошагового интегрирования системы (3.6)–(3.7) с помощью замены
ω = dφ/dt был осуществлён переход от производных по времени к производным по углу:

dv/dφ = {γR[cos(φ)·ω² + sin(φ)·f₂(φ)] + f₁(v)}/(1 - γ·sin²(φ))/ω;

(4.1)

dω/dφ = sin(φ)·(dv/dφ)/R + f₂(φ)/ω.

(4.2)

Полученные Е. Л. Таруниным уравнения движения виброхода, реализованного на базе центробежного вибратора, соответствуют трём законам Ньютона и функционально соответствуют моей модели виброхода, Программа виброхода; Движение центробежного вибратора.

Порядок счёта соответствовал записи уравнений. Из первого уравнения исключено ускорение угловой скорости. Возможно аналогичное исключение ускорения корпуса инерцоида из второго уравнения. Это не сделано сознательно – при счёте уравнения (4.2) ускорение уже известно и вычисление нового значения ω_n+1 (n – номер шага по времени) не вызывает затруднений.
      Перейдём к описанию заданных функций в (4.1), (4.2). Функция f₁(v), определяющая силу сопротивления, равна

f₁(v) = Ψ_x/M₀.

В случае кулоновского трения величина Ψ_x пропорциональна весу тела и коэффициенту трения μ:

Ψ_x = -g·μ·M₀·sign(v).

(4.3)

Следовательно,

f₁(v) =  -g·μ·sign(v) ≡  -c₁·sign(v).

(4.4)

c₁ = g·μ;     μ = c₁/g.

По данным [3] μ = (0.8 ÷ 2.5)·10^-3; согласно справочникам, значение этой величины на 1–2 порядка выше. Отсюда следует, что возможные значения коэффициента c₁ находятся в интервале 0.01 ÷ 2.5.

      Параметр c₁ по модулю – ускорение массы инерцоида под действием силы трения, так как
M₀·a = M₀·f₁(v) = Ψ_x, а  f₁(v) ≡ -c₁·sign(v). Например, в программной модели используется значение a₁ = c₁ = 2 м/с². Оценим реальность выбранного диапазона для параметра c₁.
      В. Н. Толчин в книге [3] – «Инерцоид», в явном виде не приводит значения коэффициентов μ, а только указывает трение в граммах. Для пересчёта этих значений трения к коэффициенту μ, данному в справочниках, надо учитывать роль колеса, как рычага, трансформирующего большое осевое трение на малое сопротивление обода вращению. Трение на оси, приведённое к ободу колеса получается меньше в отношении диаметра оси к диаметру колеса. Например, для "пружинного" инерцоида
k₁ = D_обода/D_оси = 30 мм/1,5 мм = 20, т. е. коэффициент трения скольжения оси в 20 раз меньше после приведения к ободу. Диапазон c₁ = 0.01 ÷ 2.5 равен диапазону коэффициента трения
μ₁ = (0.01 ÷ 2.5)/g = 0.001 ÷ 0.255, если привести этот диапазон к трению на оси, то получится
μ_ос1 = k₁·(0.001 ÷ 0.255) = 0.02 ÷ 5.1. Верхнее значение даёт трение на оси в 5.1 раз больше веса устройства, что не может быть даже без смазки (это можно сделать только специально, подобрав материал с явной целью увеличения трения). Поэтому верхнее значение коэффициента трения завышено как минимум на порядок. Например, В. Н. Толчин оценивает силу трения покоя для "пружинного" инерцоида в 25 грамм при весе 950 грамм, если пересчитать на ось, то имеем
μ = 20·25/950 = 0.526 ≈ μ_{ос_max1}/10. В движении соответственно μ = 20·6 грамм/950 грамм = 0.126. Последний коэффициент значительно больше нижней границы предлагаемой Е. Л. Таруниным. Однако В. Н. Толчин фактически оценивал трение в < 6 грамм, что указывает на его весьма критическое отношение к своим измерениям. Например, при использовании пары сталь–сталь в подшипнике скольжения, коэффициент трения будет примерно равен 0.03. При весе 950 грамм имеем трение, приведённое к ободу 0.03·950/20 = 1.425 грамм, что очёнь близко к значению средней тяги, полученной при испытании инерцоида на наклонной плоскости в 5 минут. Коэффициент связи трения и средней тяги при достаточной разности частот между медленным и быстрым полутактом незначительно отличается от единицы. В дальнейшем мы будем использовать k₁ = 20 с сопутствующими параметрами трения "пружинного" инерцоида, в качестве эталона.
      При более строгом пересчёте c₁ к μ_ос надо учитывать неравномерность распределения давления по опорной части оси. Этот коэффициент будет равен π/4 ≈ 0.785 или при обратном пересчёте 4/π ≈ 1.27. Однако это ничего принципиально не меняет.
      Если инерцоид движется на дополнительной тележке, то
k₂ = D_обода/D_оси = 50 мм/3.0 мм = 16.6(6) и μ_ос2 = k₂·(0.01 ÷ 2.5)/g = 0.0167 ÷ 4.25.
      Дополнительно для сравнения будем использовать параметры "мощного" инерцоида. К сожалению, для "мощного" инерцоида не известны параметры колеса и в этом случае мы можем использовать только μ₁ = 0.001 ÷ 0.255 в пересчёте на абсолютное трение. При весе 5600 грамм имеем 5.6 ÷ 1428 грамм. Верхнее значение не реально завышено по сравнению с оценкой В. Н. Толчина (29 гр. в покое и 10 грамм в движении). Обратите внимание, что Евгений Леонидович не отрицает возможность существования трения на нижней границе в 5.6 грамм при указанном весе. Однако при таком уровне трения (μ₁ = 0.001) ускорение программного виброхода выходит за пределы реального опыта с инерцоидом.
      Что касается трения качения твёрдого, полированного колеса по гладкой, твёрдой поверхности, то оно существенно меньше приведённого к ободу осевого трения, по крайней мере, для размеров колёс и диаметров осей которые использовал В. Н. Толчин, при его хорошем качестве изготовления. В этом можно убедится, например, испытав качественную колёсную пару на полированном стекле, вначале отдельно от тележки, а потом вместе с тележкой, т. е. при наличии осевого трения. Рассматривая трение качения, надо иметь в виду, что его определённая доля имеет упругое и гравитационное происхождение, т. е. это обратимые деформации колеса и опоры и связанные с ними микро вертикальные колебания корпуса. Эта составляющая трения создаёт на колесе силовой момент, который не приводит к потере импульса движения, но проявляет себя при измерении трения покоя.
      В уравнениях Е. Л. Тарунина масса инерцоида не используется в явном виде, так как теоретически важна только её относительная роль, как для амплитуды колебаний корпуса, так и для действия фактора трения. Это и позволяет нам использовать "пружинный" инерцоид в качестве образца осевого трения скольжения.

      Функция f₂(φ) определяет момент сил, вращающий грузики:

f₂(φ) = Ψ_φ/I,             I = 2mR².

      Функция f₂(φ) не равна нулю на двух участках: на участке торможения от φ₁ до φ₂ и на участке ускорения рычагов от φ₃ до φ₄ см.(1.1).
      На участке ускорения рычагов с грузами

f₂(φ) = c₂ – const,        φ₃ ≤ φ ≤ φ₄.

(4.5).

Значение c₂ изменялась в расчётах от 20 до 65.

Функция f₂(φ) = c₂ имеет размерность [1/с²], т. е. это угловое ускорение.
dω/dt = f₂(φ) = c₂= 20 ÷ 65 рад/с².

      На участке торможения использовались две модели – модель с постоянным тормозящим моментом и модель с трением. В модели с постоянным тормозящим моментом (первая модель)

f₂(φ) = -c₃,              φ₁ < φ < φ₂,

(4.6)

а в модели с трением (вторая модель)

f₂(φ) = -c₃·ω,           φ₁ < φ < φ₂,

(4.7)

      Часть расчётов была выполнена для значений φ₁ и φ₂, указанных в [3], хотя вычислительные эксперименты показали, что эти значения далеки от оптимальных.
      Уравнения (4.1), (4.2) определяют ускорение линейной скорости в м/с, а угловой – в рад/с; размерности величин c₁, c₂, c₃, c₄ (см. (4.4)–(4.7), (4.17)) определены из указанных связей с соответствующими силами и моментом сил.
      Перейдём к обсуждению результатов, полученных для первой модели с постоянным тормозящим моментом (4.6). В этой модели очень просто осуществляется контроль установившегося движения по выполнению интегрального закона сохранения энергии на одном периоде. На этапе разгона грузиков система получает прирост кинетической энергии, пропорциональный величине

ΔE₁ ≡ 0.5I(ω₁² - ω₀²)/M₀ = γ·R²·c₂·(φ₄ - φ₃).

(4.8)

Аналогично на этапе торможения грузиков сиcтема теряет кинетическую энергию, пропорциональную величине

ΔE₂ = γ·R²·c₃·(φ₂ - φ₁).

(4.9)

В установившемся режиме движения инерцоида разница ΔE₁ - ΔE₂ идёт на работу по преодолению силы трения (величины в (4.8)–(4.10) отнесены к полной массе M₀):

A = c₁·S,           S = x₊ - x_-.

(4.10)

      В этой формуле S – полный путь движения инерцоида за период, состоящий из двух частей: движения вперёд x₊ и движения назад (отрицательная величина) x_-.
...

      Серии вычислительных экспериментов начались для параметров (значения φ_j соответствовали (1.1))

γ = 0.3,      r = 0.3,      c₁ = 2.0,      c₂ = 20     

(4.14)

и различных значений c₃ для поиска приемлемого значения тормозящего момента. Было найдено, что максимум средней скорости v ≈ 2.01 см/с достигается при c₃ = 19 (дальнейший счёт и вёлся с этим фиксированным значением).
      Значение скоростей, получаемые при c₂ = 20, меньше тех, которые соответствуют инерцоидам. Это обстоятельство не должно смущать читателя. Нас интересуют принципиальные вопросы модели, которые могут быть рассмотрены при любых параметрах. Заметим также, что увеличение c₂ до 65 во второй модели, естественно, увеличило скорости инерцоида до параметров, близких к реальным.

К параметрам (4.14) ближе всего инерцоид "мощный". У него γ = 0.357,      r = 0.3. Он проходит за такт расстояние в S = 43 см. При переходе к программному виброходу надо уменьшить это расстояние в 0.3/0.357 = 0.84. Поэтому S = 36.12 см. При периоде T = 1.04 сек, средняя скорость будет равна v = 34.73 см/c. Этот пересчёт соответствует принципу, доказанному на опытах с "пружинным" инерцоидом, что средняя скорость равна v = S/T. Обратите внимание, что 34.73/11.67 = 2,98 ≈ 3 раза. Значение 11.67 см/с, взято из таблицы 2, ст. 218 это средняя скорость программного виброхода при периоде T = 1.04 с, в режиме слабого отката -0.15 см (при большом трении c₁ = 2 и φ₁ = 114°, т. е. с оптимизацией). Если ход за такт разделить на амплитуду инерцоида S₀ = 2·0.3·30 = 18 см., получим 36.12/18 = 2.01 ≈ 2 (для "мощного" также). Для "пружинного" инерцоида имеем ту же закономерность 60 мм/32.84 мм = 1.83 ≈ 2. Так как пересчёт от "мощного" к программному инерцоиду осуществляется примерно в пределах 16%, то нет особых оснований считать, что погрешность этого пересчёта больше этой величины. Программный виброход Евгения Леонидовича даже после оптимизации не смог достичь скорости близкой к v = 34.73 см/c. ...