|
Выше
К концу страницы
Увеличение мощности турбины с помощью вихревого генератора.
В качестве расчётной модели рассмотрим участок канала длинной \(6~м\) с прямоугольным сечением, шириной \(2~м\) и глубиной 1 метр. Скорость потока воды \(v = 1~м/с.\)
В этом канале установим турбину с входным и выходным диаметром \(d = 400~мм.\)
Перед выходным отверстием турбины находится вал диаметром \(200~мм\), вращающийся с частотой \(1.591~Гц\) (скорость вращения поверхности вала \(1~м/с.\) ).
Поток не имеет свободной поверхности, однако в более общем случае возможны варианты и со свободной поверхностью или частично.
При наличии свободной поверхности над валом образуется яма.
Боковые стенки канала без прилипания, для случая установки нескольких турбин в канале кратной ширины с общим вихревым валом.
Моделирование гидродинамики этого потока проведем на ANSYS R18 CFX. Оптимизация мощности при расчёте не проводилась.
Линии тока, идущие от входа канала и турбины.
Распределение скорости в потоке.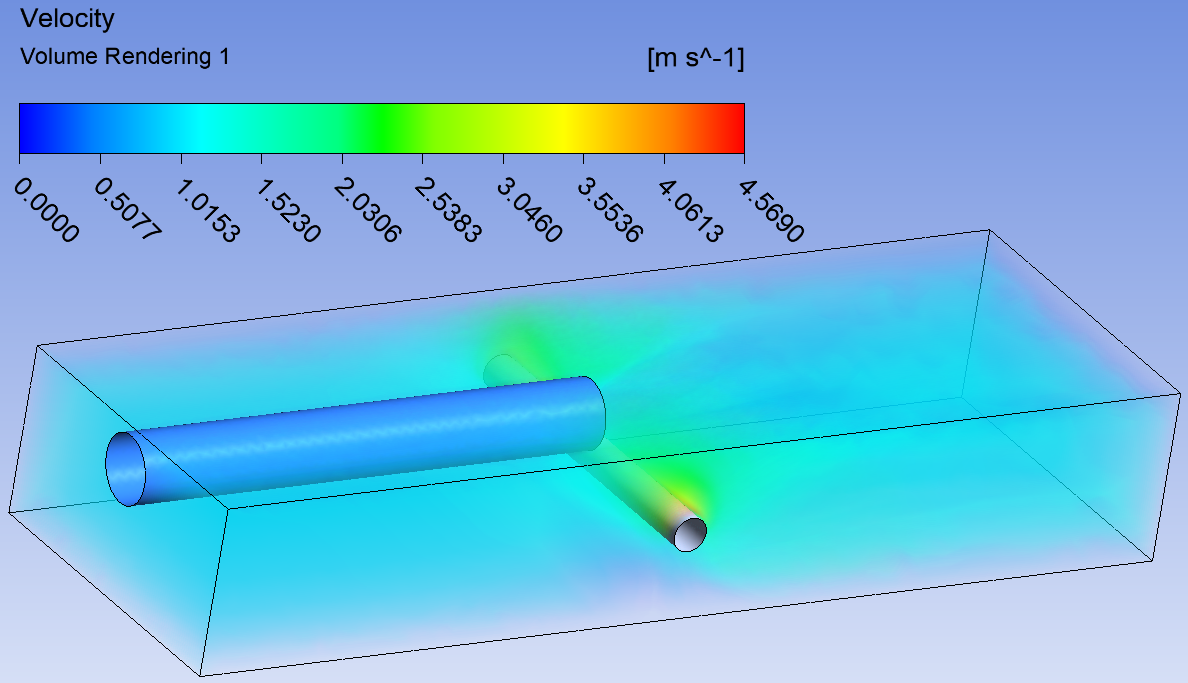
Распределение давления в потоке.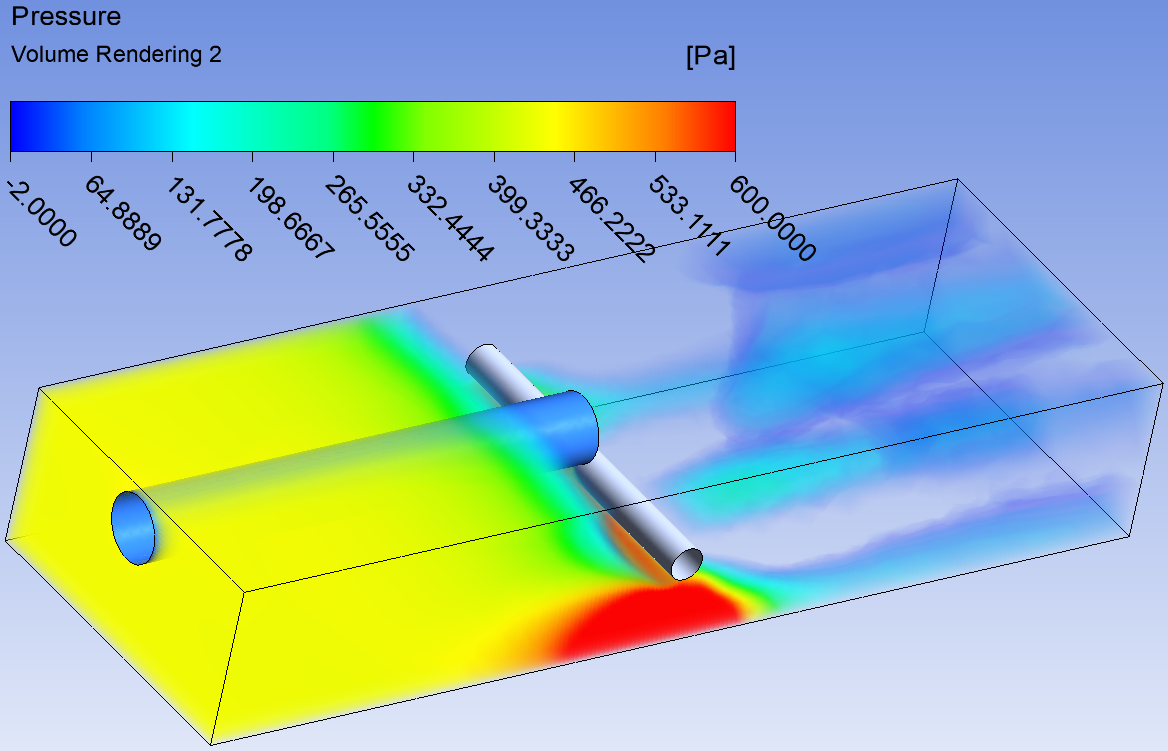
Вихревая пелена линий тока с выхода турбины.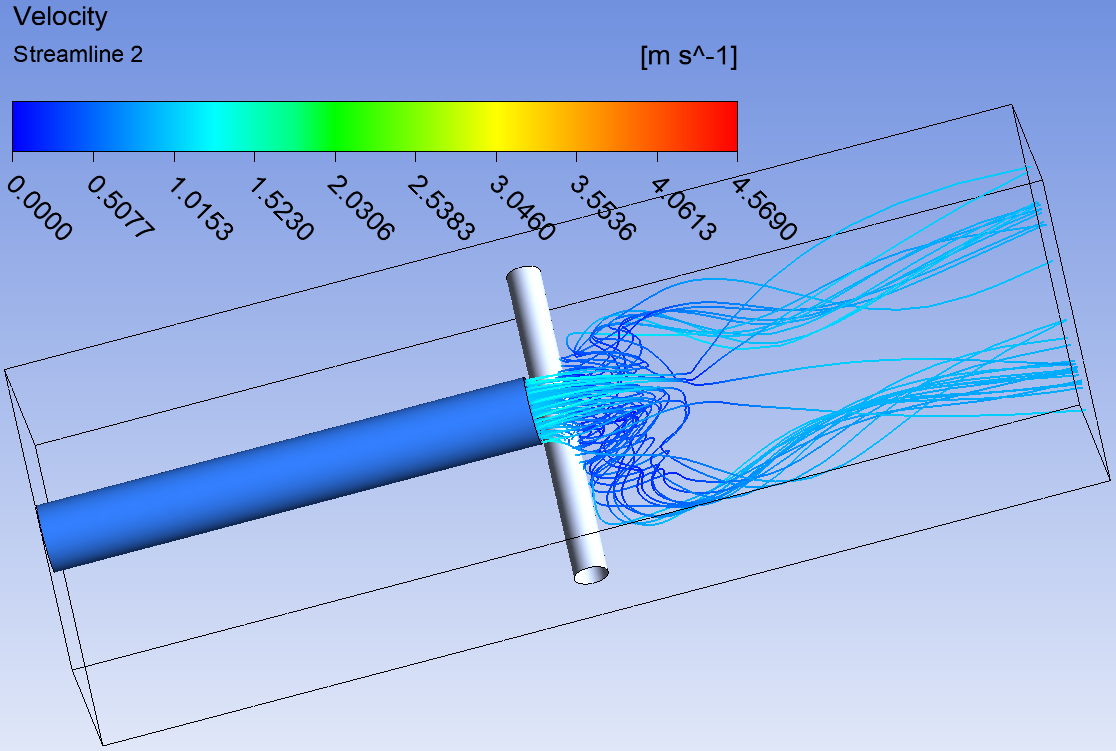
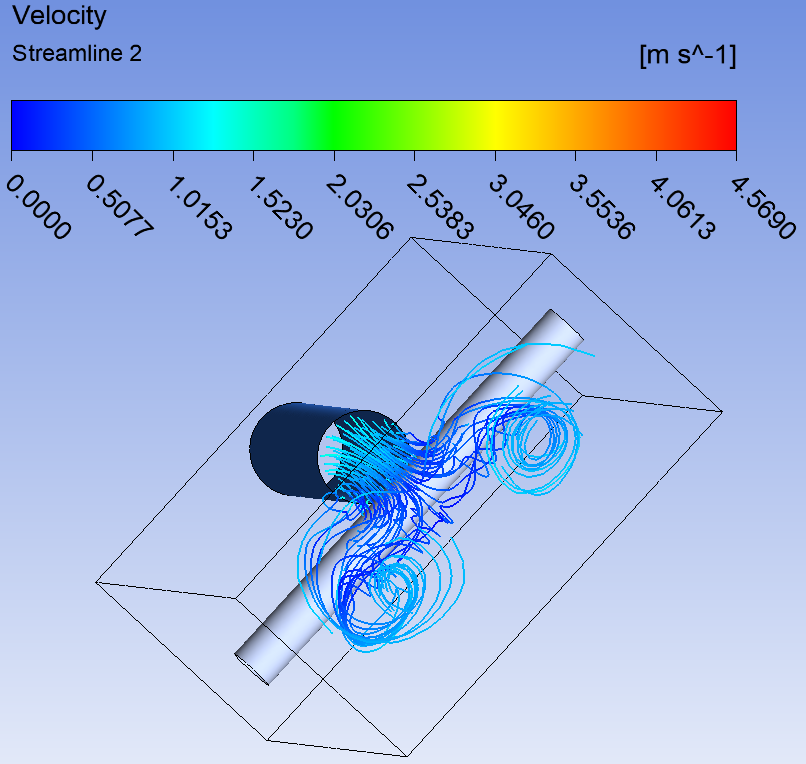
Поверхность с нулевым относительным давлением.
По результатам расчёта:
На вал действует подъёмная сила \(293~кГ\).
Среднее давление на входе турбины \(p_1 = 441.124~Па\) \((45.12~мм.~вод.~ст.)\) На эту высоту увеличивается уровень воды на входе канала.
Среднее давление на выходе турбины \(p_2 = -1255.64~ Па~(-128.43~мм. вод. ст.) \)
Разность давлений между входом и выходом \(\Delta p = p_1 - p_2 = 1696.76~Па~(173.54~мм. вод. ст.)\)
Объёмный расход через турбину \( \displaystyle Q = \frac{\pi d^2}{4} v = 0.126~м^3/c\).
Мощность турбины без учёта потерь \( \displaystyle N_v = \Delta p~Q = 213.22~Вт\).
Коэффициент усиления мощности \( \displaystyle \frac{N_v}{N_{max}} = 8.843.\)
Для сравнения вычислим максимальную мощность пропеллерной турбины, работающей на скоростном напоре.
\( \displaystyle N = Q_d \left( \frac{ \rho w_{1}^2}{2} - \frac{ \rho w_{2}^2}{2} \right) = w_2 S_2 \left( \frac{ \rho w_{1}^2}{2} - \frac{ \rho w_{2}^2}{2} \right) \) (9), где \( w_{1} = v~ - \) скорость потока в канале; \( w_{2}~ - \) скорость потока на выходе турбины;
\(\displaystyle Q_d = \frac{Q}{m} = S_1 w_1 = S_2 w_2~ - \) расход через диффузор.
Находим максимум мощности, дифференцируем выражение (9) по \( \displaystyle w_{2} \) и приравниваем к нулю
\( \displaystyle \frac{ \rho w_{1}^2}{2} - \frac{3}{2} \rho w_{2}^2 = 0;~~~~~~\) \( \displaystyle w_{1}^2 - 3 w_{2}^2 = 0;~~~~~~\) \( \displaystyle \frac{w_{1}^2}{3} = w_{2}^2.~~~~~~\) Степень расширения диффузора \(\displaystyle \frac{S_2}{S_1} = \frac{w_1}{w_2} = m = \sqrt{3}\).
Подставляем \( \displaystyle \frac{w_{1}^2}{3} = w_{2}^2 \) в выражение (9) и вычисляем мощность.
\( \displaystyle N_{max} = w_2 S_2 \left( \frac{ \rho w_{1}^2}{2} - \frac{1}{3} \frac{ \rho w_{1}^2}{2} \right) = w_1 S_1 \frac{\rho w_{1}^2}{2} \left( 1 - \frac{1}{3} \right) = \frac{2}{3} Q_d \frac{\rho w_{1}^2}{2} = 0.666(6) \cdot Q_d \frac{\rho w_{1}^2}{2} = 24.11~ Вт. \)
При отсутствии диффузора мощность будет меньше из-за потерь давления на входе турбины.
Если сечение канала заполнить подобными турбинами, то мощность без потерь будет равна \(301.4~Вт\). Например, 8 штук с диаметром 500 мм.
В случае использования вихревого вала, мощность на единицу массы конструкции будет значительно больше.
Михаил Борисович Ост. 11.12.2017 г; ред. от 14.01.2018 г.
Вариант с частично открытой поверхностью. На входе и выходе по 1.5 м открытой поверхности.
Параметры потока те же. Решение не сходится к стационарному потоку, наблюдаются пульсации.
Зона низкого давления находится под валом. Мощность турбины примерно 200 Вт без учёта потерь.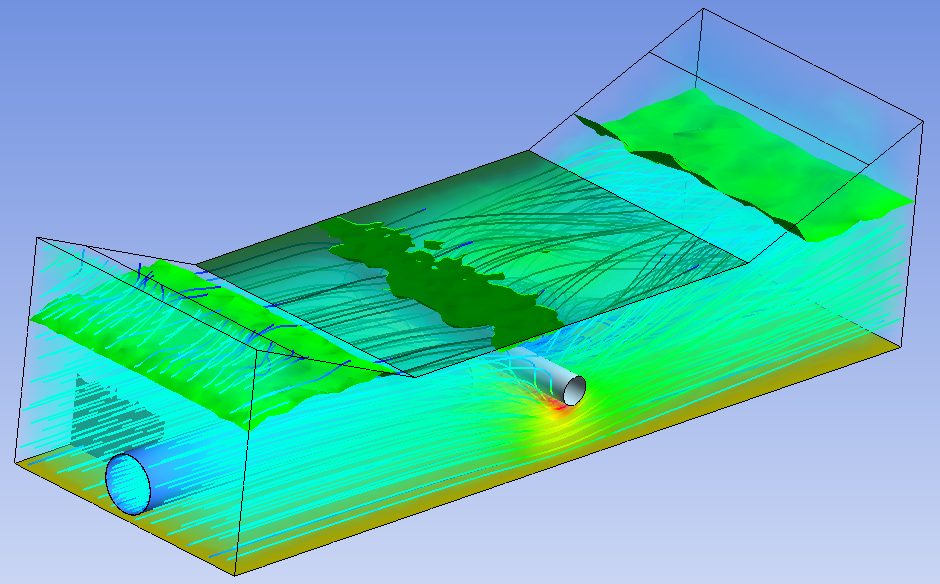
Михаил Борисович Ост. 19.02.2018 г.
Продолжение следует.
Гидравлика под ред. проф. И. И. Агроскина.
Гидравлика и гидравлические машины 1
Гидравлика и гидравлические машины 2
Гидравлика и гидравлические машины 3
Вопросы можно задавать на форуме Трансформация полной энергии потока воды.
Продолжение
Оглавление сайта
|
