Здравствуйте, Владимир Максимович. Это комментарий к вашей статье Прошу помощи!-1
    Вычисляя силу тяги, вы используете формулу q = m·ω₁²·σ²·R·sin(β), где m – масса груза;
ω₁ – угловая скорость привода, ω₁ = const; σ – коэффициент связи между углами Δα и Δβ;
R – радиус вращения грузов, R = const; β – угол, определяющий направление центробежной силы; q_y = q – проекция тяги на ось "у".
Обратите внимание, что ω₁·σ = ω – угловая скорость движения груза по круговой траектории, что следует из:
σ = dβ/dα;      dα·σ = dβ;      dα/dt·σ = dβ/dt, где dα/dt = ω₁;      dβ/dt = ω;       dβ = ω·dt.
Тогда можно записать:
q_y = m·ω²·R·sin(β). Если эту формулу разделить на массу всей установки, то получите ускорение.
a_y = (m/m₀)·ω²·R·sin(β). Зная ускорение можно вычислить скорость и перемещение. С точки зрения математики, в этом случае проще всего вычислить перемещение, через двойной интеграл.
S_y = (m/m₀)·∫∫ ω²·R·sin(β) dt dt; Сделаем замену переменной интегрирования.

S_y = (m/m₀)·∫∫R·sin(β) ω·dt ω·dt = (m/m₀)·∫∫R·sin(β) dβ dβ = (m/m₀)·R·∫∫sin(β) dβ dβ;

Обратите внимание, что этот интеграл не зависит от угловой скорости и легко берётся.

S_y = (m/m₀)·R·∫(∫sin(β) dβ) dβ = -(m/m₀)·R·∫cos(β) dβ = -(m/m₀)·R·sin(β); (1) Можно вычислить скорость.

V_y = dS_y/dt = -(m/m₀)·R·ω·cos(β);

Например, при 0° – 180° и 180° – 360°.

S_y = -(m/m₀)·R·(sin(180°) - sin(0°)) = 0; Перемещение вперёд.

S_y = -(m/m₀)·R·(sin(360°) - sin(180°)) = 0; Перемещение назад.

Вычислим импульс прибора в направлении оси "у" за полный оборот груза.
m₀·S_y = m·R·sin(β); из (1).
Тогда p = d(m₀·S_y)/dt = m₀·dS_y/dt = m·R·ω·cos(β) = m·R·ω₁·σ(β)·cos(β) = ∫q_y·dt;

Δp_y = m·R·ω₁·(σ(β₂)·cos(β₂) - σ(β₁)·cos(β₁)) = m·R·ω₁·(σ(360°)·cos(360°) - σ(0°)·cos(0°)) = 0; За полный оборот любого груза, результирующий импульс центробежной силы в направлении оси "у" равен нулю.
Таким образом, при условии R = const ваши расчёты тоже должны давать нулевую среднюю тягу. Движение, которое вы рассматриваете строго справедливо только в пределе бесконечной массы корпуса прибора или в случае многоместного движителя с бесконечным количеством мест. Ограничимся пока этим частным случаем, так как даже с этим ограничением у нас много работы. В случае конечной массы корпуса прибора, происходит перераспределение энергии между корпусом и грузами и движение усложняется.

Этот анализ показывает, что фактическая математика закона (свойства и следствия этой функции) q = m·ω²·R·sin(β) не соответствует вашим сложившимся представлениям об этом законе.

Вычислим коэффициент σ(β). Используем теорему синусов.

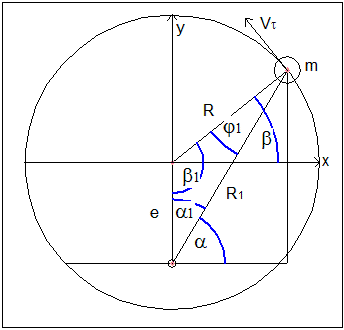
e/sin(φ₁) = R/sin(α₁), где e – эксцентриситет; R – радиус вращения груза; R₁ – вылет груза от оси привода.

α₁ = 90° - α;
sin(90° - α) = cos(α);
φ₁ + β₁ + α₁ = 180°;
φ₁ + β + 90° + 90° - α = 180°;
φ₁ + β - α = 0;
φ₁ = α - β;

e·cos(α) = R·sin(α - β); Дифференцируем это выражение по времени.

-e·sin(α)·dα/dt = R·cos(α - β)·(dα/dt - dβ/dt); dα/dt = ω₁; dβ/dt = ω; σ = ω/ω₁;

-e·sin(α)·ω₁ = R·cos(α - β)·(ω₁ - ω); Делим на ω₁.

e·sin(α) = R·cos(α - β)·(σ - 1);

cos(α - β) = cos(α)·cos(β) + sin(α)·sin(β);

e·sin(α) = R·[cos(α)·cos(β) + sin(α)·sin(β)]·(σ - 1); Делим на sin(α).

e = R·[ctg(α)·cos(β) + sin(β)]·(σ - 1);

R₁·cos(α) = R·cos(β); Вычисляем ctg(α).

R₁·sin(α) = R·sin(β) + e;

ctg(α) = cos(α)/sin(α) = R₁·cos(α)/(R₁·sin(α)) = R·cos(β)/(R·sin(β) + e);

e/R = [R·cos(β)²/(R·sin(β) + e) + sin(β)]·(σ - 1);

e/R = [R·cos(β)² + R·sin(β)² + e·sin(β)]/(R·sin(β) + e)·(σ - 1);

cos(β)² + sin(β)² = 1;

e/R = [R + e·sin(β)]/(R·sin(β) + e)·(σ - 1);

e/R·(R·sin(β) + e)/(R + e·sin(β)) = σ - 1;

σ = 1 + (e/R)·(R·sin(β) + e)/(R + e·sin(β)); (2) формула достаточно компактна для практического использования. Если отношение e/R обозначить через w = e/R, то

σ = 1 + w·(sin(β) + w)/(1 + w·sin(β)); В нашем случае w = 10/48,5 = 0,2062;

Если, σ - 1 = Δσ - относительная поправка к единице, то можно записать.

Δσ = w·(sin(β) + w)/(1 + w·sin(β)); Обратите внимание, что при e < R, что практически и соблюдается, знак поправки зависит только от числителя. Точка смены знака поправки
sin(β) + w = 0; β = -arcsin(w). По формуле это -12°, в отрицательной полу-траектории. У вас в таблице смена знака происходит в положительной полу-траектории при +12°.

Исследуем на максимум и минимум:

d(R·sin(β) + e)/dβ·(R + e·sin(β)) - (R·sin(β) + e)·d(R + e·sin(β))/dβ = 0

R·cos(β)·(R + e·sin(β)) - (R·sin(β) + e)·e·cos(β) = 0;

R²·cos(β) + R·e·cos(β)·sin(β) - R· e·sin(β)·cos(β) - e²·cos(β) = 0;

R²·cos(β) - e²·cos(β) = 0;

(R² - e²)·cos(β) = 0;

Запишем производную от σ(β), dσ(β)/dβ = (e/R)·(R² - e²)·cos(β)/(R + e·sin(β))² =
= w·(1 - w²)·cos(β)/(1 + w·sin(β))²; (3) Производная всегда отрицательна слева от оси "у" и положительна справа, т.е. слева грузы тормозятся, справа ускоряются. Через эту производную можно вычислить момент силы действующий на грузы со стороны привода.

cos(β) = 0; Это точки 90° – максимум и -90° – минимум, что соответствует геометрическому устройству системы. Коэффициент симметричен относительно оси, определяющей направление движения.
Например, σ(0°) = σ(360°) = 1 + (e/R)² = 1 + (10/48,5)² = 1,0425;
Коэффициент больше единицы, а у вас меньше единицы, т. е. вы в этом случае, фактически считаете почему-то по формуле,
σ(0°) = 1 - (e/R)² = 1 - (10/48,5)² = 0,9575; σ(0°)² = 0,917 у вас в таблице 0,915.
При σ(90°) = 1 + e/R = 1,206; σ(90°)² = 1,4549. Это значение не соответствует таблице совсем, а ведь это максимум.
При минимуме σ(-90°) = 1 + e/R*(-R + e)/(R - e) = 1 - e/R = 1 - 10/48,5 = 0,7938; σ(-90°)² = 0,6301, у вас в таблице 0,517. Таким образом, некоторая корреляция между вашими таблицами и формулой есть. Табличные значения σ(β)² должны укладываться в интервал 0,630 - 1,455. Но даже, если исправить таблицы, то существует ещё одна проблема, но это уже потом ...

Михаил Ost. 22.05.2010.
Исправлено 11.06.2010.

Ответ на Ответ-1 Владимира Максимовича Петрова.

«1. Можно, конечно, считать, что σ – это коэффициент связи между углами Δα и Δβ. Но более строгим будет определение, если считать, что σ – это отношение Δβ к Δα.»

Если строго, то σ = lim Δβ/Δα = dβ/dα. При Δβ и Δα стремящимся к нулю. Это связь между дифференциалами (производная). А ваше определение заведомо содержит не точность, так как приращения конечны. Зная σ = lim Δβ/Δα = dβ/dα можно смело писать σ·Δα = Δβ, понимая приблизительность этой связи только из-за конечного приращения Δα, а не за счёт погрешности определения σ. Коэффициент полученный из σ = Δβ/Δα имеет погрешность. Если эту погрешность можно исключить, вычислив аналитически σ = dβ/dα, то зачем её вводить в расчёт?

«2. Строго говоря, угол β не определяет выбранное направление. Этот угол, скорее, показывает отклонение вектора центробежной силы от выбранного направления.»

Согласен, есть не точность в формулировке.

«3. «Зная ускорение можно вычислить скорость и перемещение»

Не «скорость», как таковую, а в данном случае – касательную скорость. Не «перемещение», как таковое, а в данном случае – вообще непонятное перемещение по непонятному направлению.
По идее, если речь идёт о касательной скорости, то и движение должно быть по касательной. Но движения груза по касательной не может. Потому что груз-то движется по окружности!
Ваши вычисления как раз и показывают, что такого перемещения быть НЕ может!»

По вашему определению q – проекция силы тяги грузов на направление движения "у".
«Но можно смело утверждать, что всякий вектор Р можно разложить на составляющие, одна из которых (q) окажется параллельной выбранному направлению, а вторая (на схеме не показана) – перпендикулярной к нему.»
И эта проекция равна q = m·ω²·R·sin(β);

Разложение движения на ортогональные проекции в частном случае предполагает следующее:
а = i·a_x + j·a_y + k·a_z;

v = i·v_x + j·v_y + k·v_z;

s = i·s_x + j·s_y + k·s_z;

Например, мы выбрали направление j, где будем считать q/m = a_y, тогда:
v_y = ∫a_y dt; Где тут касательная скорость?

s_y = ∫v_y dt; С направлением перемещения всё в порядке!

s_y = ∫∫a_y dt dt; И ни как иначе.

Если рассмотреть все ортогональные направления сразу в сумме, то:
s = i·∫∫a_x dt dt + j·∫∫a_y dt dt + k·∫∫a_z dt dt; Зная этот вектор можно вычислить проекцию перемещения на любое произвольное направление.

s = ∫∫i·a_x dt dt + ∫∫j·a_y dt dt + ∫∫k·a_z dt dt = ∫∫(i·a_x + j·a_y + k·a_z) dt dt = ∫∫a dt dt;

s_m = m·∫∫a dt dt, где единичный вектор m – определяет произвольное направление. Это скаляр, равный проекции вектора перемещения s на направление вектора m (скалярное произведение).
Можно формально записать и в векторной форме: s_m = m·s_m;

Можно рассмотреть физическую сущность этих интегралов более подробно.
Если, a_y = ω²·R·sin(β) – проекция вектора ускорения грузов на направление движения "у", то:

v_y = -ω·R·cos(β) = -V_τ·cos(β) – это проекция вектора тангенциальной скорости грузов на направление движения "у". Так как V_τ = ω·R, при движении по окружности. Это первый неопределённый интеграл по времени от проекции вектора ускорения в направлении "у";

s_y = -R·sin(β) – Это проекция радиус вектора, т. е. фактически вектора перемещения груза на направление движения. Это второй неопределённый интеграл по времени от проекции вектора ускорения в направлении "у".

При интегрировании проекции вектора ускорения мы получаем проекцию вектора скорости на направление "у", а при интегрировании проекции вектора скорости, получаем проекцию перемещения на тоже направление, всё логично. Интегрируя проекцию q, я не выдал более того, что вы заложили в исходных данных, определив свойства этой проекции, которые я только использую в расчёте, не нарушая правил математики. Меня можно обвинить только в некотором формализме, но этот формализм тоже определён исходными данными и я не могу выйти за их пределы. Эта задача не может быть обработана абсолютно корректно, так как исходные данные поставлены искусственно. Эта искусственность обусловлена введением объекта q_y = m·ω²·R·sin(β), который по условию задачи должен создавать тягу в направлении "у", а раз должен, то к нему приходится применять соответствующие правила в соответствии с его свойствами, а как иначе? И то что это ведет к странному результату не моя заслуга. Единственный способ получить другой результат - изменить условия задачи.

«4. «траектория грузов относительно земли не будет круговой»

Грузы, вращающиеся по ПЛОСКОЙ траектории, НЕ вращаются вокруг Земли. И нет оснований считать, что при реальных размерах движителя вообще имеет смысл говорить о том, что форма траектории может почему-то отклоняться от окружности.»

Всё зависит от системы отсчёта. Если система отсчёта находится на корпусе центробежного движителя (принципиально не инерциальная), то будет окружность. Если система отсчёта (приблизительно инерциальная) связана с лабораторным столом, на котором стоит прибор, то при конечной массе корпуса движителя траектория не будет окружностью. Траектория грузов инерцоида Толчина относительно стола не окружность и это факт.

«5. «От величины массы корпуса зависит только степень этого движения»

До настоящего момента термин «степень движения» в нашем общении никак не оговаривался. Если под этим термином понимать скорость движения и/или ускорение, то я смогу согласиться с тем, что эти параметры действительно зависят от массы при заданной тяговой силе.
«а она (имеются в виду «скорость» и «ускорение») всегда в этом случае круглый ноль».

Это, как минимум, странно. Ведь тангенциальная скорость у вращающихся грузов НЕ может быть нулевой. В крайнем случае, нулевым может быть тангенциальное ускорение.
Тогда о чём идёт речь?»

Имеется в виду: скорость центра масс, перемещение центра масс, энергия относительно центра масс - центробежного мобиля (относительно внешней лабораторной системы отсчёта ). Центр масс может покоится, даже если скорости грузов и корпуса не равны нулю. Сила тяги действует на всё устройство. Я исключил это слово.

«6. «Своими опытами с центробежными движителями вы только подтверждаете этот математический факт» (эти слова исключил)
Моими опытами действительно подтверждается математический факт. Но совсем не тот, о котором говорите Вы.
Мои математические расчёты однозначно показывают, что груз элементарно НЕ УСПЕВАЕТ долететь до обечайки и посему НЕ ИМЕЕТ ВОЗМОЖНОСТИ передать через неё воздействие тяговой силы.»

Если груз движется вдоль спицы свободно, без сопротивления и силового момента со стороны привода, то центробежной силы просто нет. Центробежная сила возникает, при условии, что есть сопротивление вдоль спицы (упор), тогда траектория деформируется и следствием этого, при наличии энергии груза, является центробежная сила. Груз, свободный от сопротивления вдоль спицы, не может двигаться по окружности и формула q = m·ω²·R в этом случае работает в других условиях. Ваши табличные расчёты в статье «Прошу помощи!-1» и в моих комментариях к этой статье теряют смысл в этих условиях. Эти расчёты справедливы только для схемы, где грузы жестко движутся по направляющим, образующим окружность.

«7. «Вычислим импульс прибора…»

Под термином «импульс прибора» вероятнее всего имеется в виду «импульс силы». Если предполагается именно это, то необходимо знать величину перемещения, реализованного известной массой. Вы проверяете импульс силы по тангенциальному (не существующему) перемещению. Разумеется, импульс в этом случае ОБЯЗАН быть нулевым.
Только какое отношение это имеет к перемещению мобиля?»

Импульс силы в данном случае это интеграл ∫q_y·dt (и другого импульса силы в системе нет, это единственный источник) и этот интеграл в общем случае не равен нулю, для его вычисления не обязательно знать перемещение. Я проверяю действие импульса силы по проекции вектора тангенциальной скорости грузов в направлении "у". Проекцию тангенциальной скорости, вычисляю дифференцированием перемещения, так как это проще.
v_y = -ω·R·cos(β) = -V_τ·cos(β); Эта скорость грузов (проекция ) формируется ускорением
а_y = q/m.
Результат действия импульса силы в направлении "у" реализуется в проекции вектора скорости грузов в этом направлении ∫q_y·dt = m·v_y; При этом грузы одновременно являются источником импульса силы для всей системы масс центробежного мобиля (источник единственный). Грузы ускоряют себя в направлении "у" и тянут корпус. Поэтому скорость центра масс мобиля относительно стола будет равна (∫q_y·dt)/m₀= (m·v_y)/m₀ = v. Эти рассуждения справедливы только при условии, если масса корпуса стремится к бесконечности. В противном случае происходит перераспределение энергии между корпусом и грузами и движение усложняется. Однако это ограничение не является принципиальным в теоретическом плане, т. е. позволяет однозначно определить теоретическую возможность (или не возможность) движения мобиля, что по минимуму нам пока достаточно. Другим предельным случаем, который позволяет упростить анализ, это использовать идею о многоместном мобиле. Если взять мобиль с бесконечным количеством мест, то вибрации корпуса не будет и соответственно при малой тяге, мы можем пренебречь перераспределением энергии между грузами и корпусом, что с некоторыми поправками эквивалентно свойствам модели с бесконечной массой корпуса. Если вы с этой схемой движения не согласны, то мне интересно увидеть ваш вариант.

«8. «Этот анализ показывает, что…»

Тяговая компонента от центробежной силы определяется формулой:

q = m·ω²·R·sin(β);

и эта формула никак не связана с моими представлениями о законе, относящемся к генерации центробежных сил.
Думать по этому поводу я могу что угодно. Но вычислять нагрузку на рельсы в поворотном участке железнодорожного пути я вынужден именно по этой формуле. По этой же формуле я обязан вычислять нагрузку на коленчатый вал. Амплитуду вибратора… И, так далее.
Именно по этой формуле я вычислял, вычисляю и ДОЛЖЕН буду вычислять центробежную силу для ВСЕХ своих разработок.»

Пожалуй, это самый сложный пункт. Для его комментария необходимо углубится не только в механику и математику, но и в философию механики. Признаю, что пока не готов понятно выразить это в словах.

9. Вставил рисунок и дополнил.

«10. В моей статье «ПРОШУ ПОМОЩИ! – 1» приведены 8 условных подразделов.
В КАКОМ из этих подразделов я проявил неправильное понимание?»

Для начала, кратко пройдемся по вашим пунктам 1 – 8.

1.«Лично я считаю, что после обрыва нитки камешек полетит по прямой, проходящей через ось вращения и через точку, в которой находился центр массы шарика в момент обрыва нитки.»
Камешек полетит по касательной, которая определяется моментом отрыва.

2. Нет возражений.

3. Ваш вариант правильный, однако, эту задачу можно решать и из точки вращения привода.

4. Нет возражений.

5 – 6. Трудоёмкий и не надежный метод расчёта. Ошибка есть, но для её локализации надо всё просчитать самому. Проще вычислить аналитически, чем искать ошибку. Проверьте знаки, так как при сравнении с аналитической формулой, есть не совпадение именно в знаках.

7. Качественно, график построен правильно, но есть проблема с усреднением. Это требует специального обсуждения. Если подробнее, то с усреднением тяги связано две проблемы, обе касаются интегрирования. Первая проблема, это правильный выбор метода усреднения. Вторая, непосредственно касается составления интеграла, который должен удовлетворять механике этого движения.

8. Тяга относительно центра масс в пределах погрешности будет равна нулю, если поправить таблицы и правильно усреднить тягу.

Пункт 1 не влияет на вычисления, поэтому можно начать работу с пунктов 5–6.

Михаил Ost. 29.05.2010.

Ответ на Ответ-2 Владимира Максимовича Петрова.

Владимир Максимович, идём по вашим пунктам в Ответе-2. Ответы по мере возможности и не порядку. С моими статьями, направленными к вам, вы можете делать всё что угодно, однако проблема в том, что я буду их иногда редактировать и поэтому для поддержания их актуальности с вашей стороны, потребуется дополнительная работа. Например, мне не нравится самое начало этой статьи, я хочу ограничить свою задачу пока только анализом вашей методики расчёта тяги, не анализируя реальное движение вашего варианта центробежного движителя, так как в простом виде это не получается.

1. «Что будет с величиной перемещения мобиля, если рассмотреть диапазон не от 0º до 180º, а от 0º до 90º?
S_y = -(m/m₀)·R·(sin(90°) - sin(0°)) = -(m/m₀)·R» (у вас потерян знак минус, но это не так важно по сравнению с ...)
Теорема о разбиении интеграла. При любых числах a, b, c
^b∫_a f(x) dx = ^c∫_a f(x) dx + ^b∫_c f(x) dx.
Вы эту теорему не соблюдаете. Не может существовать ни каких дополнительных обоснований, оправдывающих не соблюдение теоремы. Для природы это общий закон суммирования.
S_y = -(m/m₀)·R·(sin(180°) - sin(0°)) = -(m/m₀)·R·[( sin(90°) - sin(0°) ) + ( sin(180°) - sin(90°) )] =
= -(m/m₀)·R·[(1 - 0) + (0 - 1)] = 0.

1.1 «Направление вектора центробежной силы всегда исходит из оси вращения груза».

В общем случае центр вращения груза может не совпадать с физической осью. В этом частном случае совпадает. Например, у инерцоида Толчина грузы в конце траектории резко разворачиваются. Относительно лабораторной системы отсчёта (стола) радиус вращения грузов получается значительно меньше конструктивного радиуса.

1.2 «Я имею право считать, что в некоторый момент времени направление вектора отклонилось от горизонтальной оси на угол β».
Все, что наблюдается в реальном движении может быть формализовано соответствующими переменными. Вы считаете совершенно правильно.

1.3 – 1.6 Формально, по математике возразить нечего.

1.7 «Не надо иметь семь пядей во лбу, чтобы признать, что площадь под ВЫПУКЛОЙ вверх кривой НЕ МОЖЕТ быть ни нулевой, ни отрицательной. А, следовательно, НЕ МОЖЕТ быть нулевой и генерируемая тяговая сила в первом полуобороте груза».
Обратите внимание, что грузы по окружности движутся с ускорением, а значит, существует момент силы со стороны привода, который их ускоряет и тормозит, в соответствии с заданным вами законом движения. Грузы на привод, действуют противоположным моментом. Таким образом, на груз действуют две силы. При строгом подходе к решению этой задачи мы должны учитывать все реальные силовые факторы. Пренебрегать силовыми факторами можно только убедившись в их малой значимости, т. е. мы должны решать эту задачу с полным набором сил, а это в корне меняет ситуацию. В этом случае площадь под кривой уже будет другой, так как появится дополнительное слагаемое к проекции силы на ось "у".
Эта сила равна:
q_2y = -m·R·(dω/dt)·cos(β) – проекция силы действующей на привод со стороны груза. Тогда полный импульс силы равен:
p_y = m·R·∫( ω²·sin(β) - (dω/dt)·cos(β) ) dt = -m·R·ω·cos(β). Можно проверить дифференцированием. Это решение мы получили в начале статьи. На замкнутой траектории этот интеграл даёт нулевое значение.

1.8 «ПОЛОЖИТЕЛЬНАЯ усреднённая и не скомпенсированная тяговая сила, воздействующая на корпус мобиля, ОБЯЗАНА придать корпусу ускорение (или, как минимум, - СКОРОСТЬ). При этом скорость НЕ МОЖЕТ равняться нулю до тех пор, пока не равна нулю тяговая сила».
Наличие скорости у корпуса и грузов не означает, что их центр масс имеет скорость. А вот то что помечено красным в общем случае неверно, так как тяга и скорость отличаются на один дифференциальный порядок и в результате фазового сдвига между ними одна величина уже стала нулевой, а другая ещё не успела. ...

1.9 Совместно с моментом уменьшит до нуля.

1.10 При уменьшении угловой скорости время нахождения в зоне отрицательной тяги увеличивается, что компенсирует потерю силы так как дифференциал импульса силы равен dp = q·dt.

«Следовательно, Автору необходимо простым методом показать, что угловая скорость груза в его отрицательном полуобороте не уменьшается».
Не могу пока точно утверждать, так как ещё не до конца продумал, но по всей видимости, можно показать, что изменение угловой скорости на самом деле есть математическая иллюзия. Это косвенно подтверждается тем фактом, что ваш реальный центробежный движитель данной конструкции не разгоняется.

«Если не получится доказать это, то придётся признать, что по причине уменьшения угловой скорости в отрицательном полуобороте груза уменьшается и отрицательная усреднённая тяговая сила».
Это высказывание и предыдущее в этом пункте, как ни странно, не связаны между собой, сила реально уменьшается, так как радиус движения становится меньше при тех же оборотах.

1.11 «Относительно использования интегрального исчисления для выявления усреднённой тяговой силы, ПОЛЕЗНО ВСЕГДА ПОМНИТЬ о том, что процесс интегрирования – это ВСЕГДА процесс нахождения первообразной функции, каковой усреднённая тяговая сила НЕ является.»
Определённый интеграл это в первую очередь сумма, составленная по правилам, а нахождение первообразной это способ аналитически вычислить эту сумму через разность первообразных при разных значениях аргумента.

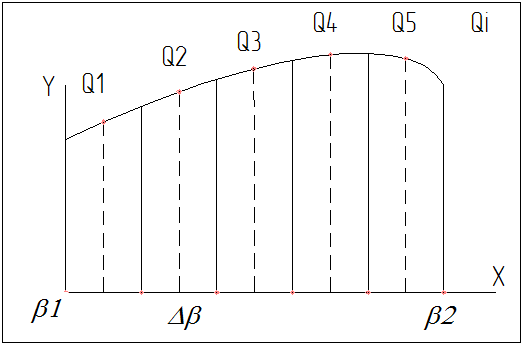
Вы, вычисляете среднее значение по формуле: Q_s = _i=1∑ⁿ Q_i/n.
Если существует n чисел, то для нахождения их среднего значения надо найти сумму этих чисел и разделить на их количество.

Если, Δβ – постоянный шаг усреднения, в вашем случае Δβ = 3°;

Δβ₂₁ – интервал усреднения, в вашем случае [β₁, β₂] = [0°, 180°], Δβ₂₁ = β₂ - β₁ = 180°;

Δt₂₁ = t₂ - t₁ - интервал времени для интегрирования;

Δα₂₁ = α(β₂) - α(β₁) - угол поворота привода при повороте груза на Δβ₂₁;

Δα₂₁ = ω₁·Δt₂₁; так как ω₁ = const.

Q_i·Δβ – площадь элементарного прямоугольника под функцией;

_i=1∑ⁿ Q_i·Δβ – вся площадь под функцией с погрешностью дискретизации, то

(_i=1∑ⁿ Q_i·Δβ)/Δβ₂₁ = (_i=1∑ⁿ Q_i)·Δβ/Δβ₂₁ = (_i=1∑ⁿ Q_i)/n = Q_s, где n = Δβ₂₁/Δβ – количество элементов на интервал усреднения, в вашем случае должно быть n = 60. У вас 59, что не принципиально, так как это зависит от тонкостей способа дискретизации, который вы выбрали, при этом не зависимо от способа в пределе n → ∞ будет тот же результат.

Так как по определению интеграла.
lim_i=1∑ⁿ Q_i·Δβ = ^β2∫_β1 Q dβ, при n → ∞ и Δβ →0, то
Q_s = lim (_i=1∑ⁿ Q_i·Δβ)/Δβ₂₁ = (^β2∫_β1 Q dβ)/Δβ₂₁;

Поэтому определённый интеграл и среднее значение связаны между собой и если
^β2∫_β1 Q dβ = 0, то и среднее значение тоже равно нулю.

Осуществляя усреднение необходимо правильно выбрать этот интеграл. Принцип усреднения должен соответствовать физическому смыслу. В механике для этого случая есть два основных интегральных выражения.
Импульс силы р = ∫q_y·dt и работа A = ∫ q_y·ds.

Нам больше подходит импульс силы, так как с временем мы более определены (и др. причины есть и среди них принципиальные, которые нельзя игнорировать).
Q_s = (^t2∫_t1 q_y·dt)/Δt₂₁ = m·R·(^t2∫_t1 ω²·sin(β) dt)/Δt₂₁ = m·R·(^β2∫_β1 ω·sin(β) dβ)/Δt₂₁ =
= m·R·ω₁·(^β2∫_β1 σ(β)·sin(β) dβ)/Δt₂₁ = m·R·ω₁²·(^β2∫_β1 σ(β)·sin(β) dβ)/Δα₂₁.

В вашем случае получается совсем другой интеграл.
Q_s = (^β2∫_β1q_y·dβ)/Δβ₂₁ = m·R·(^β2∫_β1 ω²·sin(β) dβ)/Δβ₂₁ = m·R·ω₁²·(^β2∫_β1 σ(β)²·sin(β) dβ)/Δβ₂₁ и он не даёт действующего значения тяги.
Правильное, действующее значение средней тяги равно
Q_s = m·R·ω₁²·(^β2∫_β1 σ(β)·sin(β) dβ)/Δα₂₁ и ни как иначе. Это вопрос принципиальный.
Например, при измерении напряжения переменного электрического тока, используется несколько методов усреднения и каждый из этих методов имеет свой физический смысл и в некоторых случаях, может получится большая погрешность измерения, если не учитывать принцип работы схемы прибора и характер сигнала.
Однако, есть ещё одна проблема в вашей методике расчёта тяги и рассматривать эту проблему имеет смысл только при условии, что расчёт средней тяги будет осуществляться по формуле
Q_s = m·R·ω₁²·(^β2∫_β1 σ(β)·sin(β) dβ)/Δα₂₁. В противном случае физика и математика принципиально не стыкуются. Используемая вами величина средней тяги просто не отражает сущности этого механического явления, она искусственна и формальна. Если говорить образно, то ваш "вольтметр", показывает цену на дрова. ...

2. Я имел в виду формулу σ(β) = 1 + w·(sin(β) + w)/(1 + w·sin(β)), которая позволит упростить таблицы.

3.1 Представьте себе, что на верёвочке вращается грузик с постоянной по модулю скоростью. Разместим в центре вращения систему координат x, y. Если известна V – окружная скорость грузика, то можно рассчитать его импульс в любой точке траектории по осям x, y.
p_x = m·V·sin(β), где β – угол между верёвкой и положительной осью "x".
p_у = m·V·cos(β);
Предположим, что в момент пересечения оси "у" грузик оборвался и полетел вдоль оси "у". Так как вдоль оси "у" действует центробежная сила, то по вашим предположениям он получил импульс от этой центробежной силы равный p_у = m·V. Однако грузик изменил скорость и в направлении оси "x", так как не полетел в её направлении. До момента обрыва верёвки он имел импульс p_x = m·V·sin(90°), а после обрыва p_x = 0, так как уже летит в направлении оси "у". Однако в направлении оси "x" нет сил. Если нет сил, то почему грузик изменил импульс в направлении оси "x"?

Михаил Ost. 14.06.2010.

Продолжение

Главная страница