|
Механическая работа воды в аномальной зоне расширения от 4° до 0° с возможной частичной кристаллизацией.
Я обращаю ваше внимание на формальную возможность, предположить, что такая работа возможна, а вот, что получается на самом деле, мы постараемся разобраться в процессе анализа.
Так как вода расширяется при понижении температуры после 3,98°, то её можно заставить в этой зоне совершать положительную работу. Однако для этого необходимо очень большое рабочее давление, чтобы при малом температурном коэффициенте расширения воды обеспечить её эффективную работу. Работа физически определяется как произведение давления на приращение объёма
A = p·ΔV. Поэтому для получения реальной работы при малом изменении объёма необходимо большое давление. Любые разговоры о работе воды за счёт внутренней энергии при расширении, вне этой простой формулы, лишены физического смысла.
Второе условие – вода должна при высоких давлениях сохранять свойство расширятся после 4°, в достаточной степени для реальной работы, что и требует проверки.
Определимся с теорией.
m = ρ·V; V = m/ρ (1), где m – масса воды; V – объём воды.
Найдём дифференциал объёма, дифференцируя (1)
dV = -(m/ρ2)·dρ;
По определению коэффициент объёмного теплового расширения равен
βT = (1/V)·dV/dT = (ρ/m)·(m/ρ2)·dρ/dT = -(1/ρ)·dρ/dT.
Коэффициент сжимаемости равен
βp = -(1/V)·dV/dp = (ρ/m)·(m/ρ2)·dρ/dp = (1/ρ)·dρ/dp;
dρ/dT = -ρ·βT;
dρ/dp = ρ·βp.
Дифференциал плотности от функции двух переменных p и T можно записать так
dρ = ρ·βp·dp - ρ·βT·dT.
Запишем дифференциал работы
dA = p·dV = -p·(m/ρ2)·dρ = -p·(m/ρ2)·(ρ·βp·dp - ρ·βT·dT) = -p·(m/ρ)·(βp·dp - βT·dT);
dA = -p·V·(βp·dp - βT·dT) = -K·Cp·m·dT, где K – коэффициент, показывающий какая доля теплоты при охлаждении воды пошла на работу.
dA = -p·V·(βp·dp - βT·dT) = -K·Cp·ρ·V·dT;
p·(βp·dp - βT·dT) = K·Cp·ρ·dT;
p·(βp·dp/dT - βT) = K·Cp·ρ;
K = p·(βp·(dp/dT) - βT)/(Cp·ρ).
Для изобарного процесса
K = -p·βT/(Cp·ρ).
Для начала рассмотрим задачу в изобарном варианте при нормальном давлении. В этом случае работа будет очень маленькой, но нам важно определить сам факт возможности полезной работы.
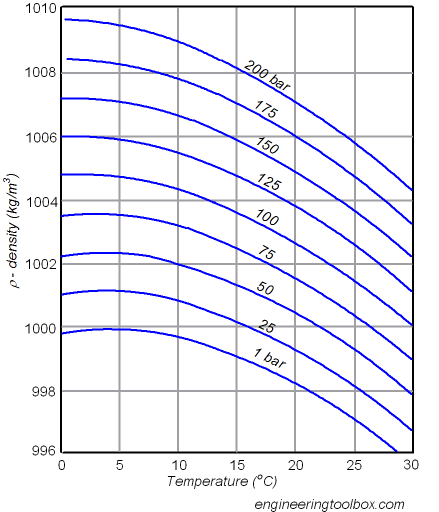
Плотность воды при нормальном давлении.
-10° 998,15 кг/м3
-5° 999,30
0° 999,87
+4° 1000,00
+5° 999,99
+10° 999,73
dρ = kT·dT – зависимость дифференциала плотности от дифференциала температуры в линейном варианте, ρ – плотность; T – температура; kT – коэффициент изменения плотности от температуры.
kT = dρ/dT = (1000,00 - 999,87)/4° = 0,13/4° = 0,0325. Для интервала температур от 0° до 4° по таблице.
βT = -kT/ρ = -0,0325/1000 = -0,325·10-4.
K = -p·βT/(Cp·ρ) = 101325·0,325·10-4/4200/1000 = 0,0000007840625. Столь маленький коэффициент преобразования внутренней энергии в работу фактически означает невозможность даже теоретически получить полезную работу в замкнутом цикле.
Рассчитаем прирост скорости потока воды в трубе при охлаждении. Избыточное давление в потоке до зоны ускорения 1 атм
m·v2/2 - m·v02/2 = K·Cp·m·ΔT; v2/2 = K·Cp·ΔT, где v0 – начальная скорость воды. При маленькой начальной скорости можно записать
v1 = √(2·K·Cp·ΔT) = √(2·0,0000007840625·4200·1°) = 0,081 м/с на 1°. На 4° 0,162 м/с. Если не уменьшить сечение трубы, то возможен переход в турбулентное состояние.
При 25 атм будет
v2 = √(25·2·0,0000007840625·4200·1°) = 0,405 м/с на 1°. На 4° 0,811 м/с.
Сделаем формальный расчёт при 900 ат. В этом случае βT = +2,29·10-4. Аномалии плотности уже нет.
K = -p·βT/(Cp·ρ) = -900·101325·2,29·10-4/4200/1000 = -0,0049721625. Если не обращать внимания на знак, то и в этом случае коэффициент преобразования очень мал.
При рассмотрении таких случаев надо учитывать не только этот процесс работы, но весь термодинамический цикл в целом, который в данном случае содержит процессы чисто механического сжатия и расширения воды, которые имеют к.п.д. меньше единицы в силу неизбежных потерь энергии на трение и удар. Дополнительно ещё требуется цикл работы по охлаждению воды, где тоже есть потери. Совершаемая работа должна быть больше энергетических потерь в системе.
Рассмотрим случай переменного давления
K = p·(βp·(dp/dT) - βT)/(Cp·ρ).
Из формулы видно, что при (dp/dT) > 0 можно увеличить коэффициент преобразования. Однако, это только формально прибавляет работу, так как сжатие связано с упругими взаимодействиями и в процессе термодинамического цикла в среднем даёт нулевую работу.
Рассмотрим, что будет при больших давлениях.
Температура, при которой вода имеет максимальную плотность при различных давлениях, определяется формулой
T = 3,98° - 0,0225·(p - 1), где p – давление в атм.
Например, при p = 150 атм; T = 0,63°. Температура максимальной плотности сильно зависит от давления, что фактически делает предположение о возможности использовать полный диапазон температур от 4° до 0° для совершения работы при больших давлениях не возможным. Температура максимальной плотности стремится к точке замерзания. ...
Рассмотрим фазовую диаграмму воды.
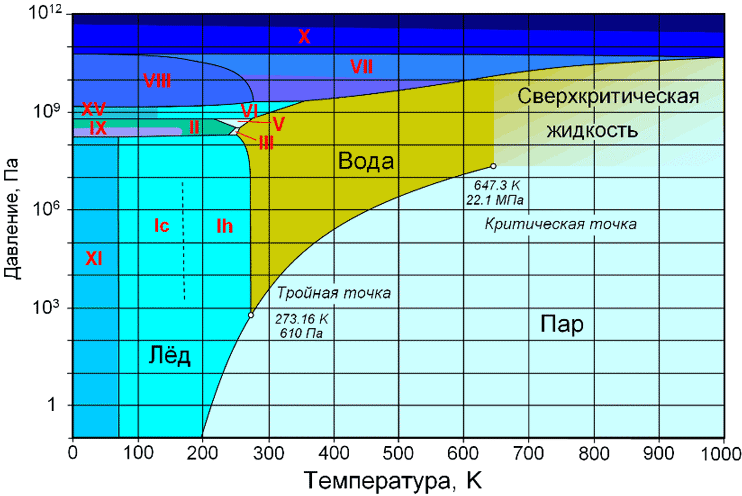
Зависимость коэффициента теплового расширения воды от давления и температуры
| Давление |
Коэффициент объёмного теплового расширения β, 1 / K при разных температурах |
| Па |
ат |
0°С .. 10°С |
10°С .. 20°С |
20°С .. 50°С |
60°С .. 70°С |
90°С .. 100°С |
| 9.81·104 |
1 |
0.14·10-4 |
1.50·10-4 |
4.22·10-4 |
5.56·10-4 |
7.19·10-4 |
| 9.81·106 |
100 |
0.43·10-4 |
1.65·10-4 |
4.22·10-4 |
5.48·10-4 |
— |
| 19.62·106 |
200 |
0.72·10-4 |
1.83·10-4 |
4.26·10-4 |
5.39·10-4 |
— |
| 49.05·106 |
500 |
1.49·10-4 |
2.36·10-4 |
4.29·10-4 |
5.23·10-4 |
6.61·10-4 |
| 88.29·106 |
900 |
2.29·10-4 |
2.89·10-4 |
4.37·10-4 |
5.14·10-4 |
6.61·10-4 |
Средний коэффициент объёмного теплового расширения воды в диапазоне от 4° до 10° равен
βT = -(dρ/dT)/ρ = -(999,73 - 1000,00)/6°/1000 = 0,27/6°/1000 = 0,45·10-4.
Ранее посчитанный коэффициент расширения воды в диапазоне от 0° до 4° равен
βT = -0,325·10-4.
В таблице приведённой выше при 1 ат стоит коэффициент 0,14·10-4. Этот коэффициент был вычислен без учёта аномалии т. е.
βT = -(dρ/dT)/ρ = -(999,73 - 999,87)/10°/1000 = 0,14/10°/1000 = 0,14·10-4.
Поэтому начало колонки от 0° до 10° фактически не учитывает аномалию. Аномалия плотности исчезает в диапазоне давлений 100 – 200 ат и средние коэффициенты в таблице при давлениях 200 – 900 ат уже вполне корректны. ...
Существует гипотеза, что вихревое движение воды в определённых условиях может упорядочивать молекулярную энергию, увеличивая энергию потока. Рассмотрим возможные варианты этого пока предполагаемого явления.
Вода имеет сложную структуру, поэтому можно предположить, что в структуре воды существуют локальные образования, имеющие разную плотность в силу отличия в упаковке молекул. Если эти образования достаточно большие, то теоретически становится возможна их сепарация в вихре. Плотные структуры идут к периферии легкие фракции к центру. Расслоение имеет определённые термодинамические последствия, так как исходная вода находилась в равновесии. Образовавшиеся неравновесные фазы должны изменить свои термодинамические параметры при переходе к новому равновесию, т. е. фактически изменить температуру и плотность. Изменение плотности вызывает динамическое движение, которое мы уже частично рассмотрели. Если рассматривать воду с температурой выше 4°, то центральная лёгкая фракция, будет сжиматься, и температура её будет понижаться, а периферийная тяжёлая фракция расширяться с повышением температуры в соответствии с функцией ρ = f(p,T) для воды. Понижение температуры в центре согласуется с информацией, которую можно прочитать в интернете. В результате в центре вихря происходит торможение потока, а на периферии ускорение потока. При этом центральное торможение способствует периферийному ускорению, так как создает дополнительный напор (как пробка). Можно даже сделать смелое предположение, что фазовый переход на периферии хорошо катализируется некоторыми материалами, например медью. Поэтому явление и проявляет себя в медных трубах. Перераспределение энергии по сечению вихря ещё не означает увеличения результирующей энергии, однако вселяет надежды на это. ...
Первый закон термодинамики
Первый закон термодинамики представляет собой частное выражение более общего закона природы – закона сохранения энергии и формулируется следующим образом: разные формы энергии переходят друг в друга в строго эквивалентных, всегда одинаковых соотношениях.
Отсюда вытекает, что в любой изолированной системе общий запас энергии остаётся постоянным.
...
Согласно первому закону, если теплота превращается в работу или работа в теплоту, то количество механической работы эквивалентно количеству теплоты. Соотношение между теплотой q и работой A при изменении общей энергии системы ΔU устанавливается первым законом термодинамики.
Так как в изолированной системе внутренняя энергия является постоянной величиной, то в любом процессе изменение внутренней энергии ΔU какой-нибудь системы равно разности между количеством сообщенной системе теплоты и количеством работы, совершенной системой, т. е.
ΔU = q - A (10)
Для бесконечно малого изменения состояния, изменения внутренней энергии, теплоты и работы будут бесконечно малыми, и в этом случае уравнение (10) принимает вид:
dU = dq - dA (11)
Уравнения (10) и (11) являются математическим выражением первого закона термодинамики.
Изменение внутренней энергии системы может происходить в результате поглощения и выделения системой теплоты или выполнения работы.
Из уравнений (10) и (10) следует, что если работа совершается только против внешнего давления, то для изобарного процесса
A = p·ΔV, или dA = p·dV (12)
В этом случае для изохорного процесса (dV = 0) получим:
q = ΔU, или dq = dU (13)
Из уравнений (11) и (12) имеем:
ΔH = ΔU + p·ΔV, или dH = dU + p·dV (14)
С. А. Балезин; Б. В. Ерофеев и Н. И. Подобаев., Основы физической и коллоидной химии, Москва, "Просвещение", 1975, ст. 47 - 48.
ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
Первый закон термодинамики является частным случаем закона сохранения и превращения энергии. Он представляет собой приложение этого фундаментального закона к термодинамическим системам.
Закон сохранения энергии гласит, что сумма всех видов энергии изолированной системы есть величина постоянная, т. е. ∑dEi = 0, или ∑Ei = const, где Ei – виды энергии.
Пусть в некоторой термодинамической системе, состоящей из рабочего тела и окружающей среды, энергия передаётся от окружающей среды к рабочему телу. В общем случае энергия передаётся в форме теплоты и в форме работы. Следовательно, приращение энергии рассматриваемого рабочего тела будет равно сумме количеств энергии, переданных ему в форме теплоты Q и в форме работы L, т. е.
ΔE = Q + L. (1.21)
Работу L окружающей среды над рабочим телом можно заменить работой преодоления рабочим телом сил окружающей среды, которая будет численно равна L, но противоположна по направлению, т. е. со знаком минус; обозначим её L*. Тогда уравнение (1.21) перепишется так:
Q = ΔE + L*. (1.22)
Это уравнение и есть математическое выражение первого закона термодинамики. Таким образом, первый закон термодинамики можно сформулировать так: количество энергии, подведённой к телу в данной термодинамической системе в форме теплоты, идёт на изменение его энергии и на совершение этим телом внешней работы.
Энергию тела E можно рассматривать состоящей из внешней Eв и внутренней U энергий, т. е.
E = Eв + U.
Внешняя энергия тела Eв представляет собой сумму кинетической и потенциальной энергий этого тела. Первая из них, если пренебречь кинетической энергией вращения тела вокруг центра инерции, равна mc2/2, где c – скорость центра инерции тела, м/с; m – масса тела, кг. Единица кинетической энергии – кг·м2/c2 = Н·м = Дж. Вторая составляющая внешней энергии тела – внешняя потенциальная энергия – равна mgH, где g – ускорение свободного падения, м/c2; H – высота, м.
Следовательно, в общем случае изменение внешней энергии тела
ΔEв = m(c22 - c12)/2 + mg(H2 - H1). (1.23)
...

| 
