Выше

От 08.11.10

          Михаил, спасибо за оперативный ответ!

          Мне показалось, что мы в чём-то недопоняли друг друга. Я испрашивал Вашего мнения о гравитационном моторе, а Вы закомментировали какую-то статью (может быть, даже, и мою) о центробежном движителе (ЦД).
          Я допускаю, что движитель, Вами закомментированный, работает (или НЕ работает) именно так, как Вы и представили, но предложенный мною для обсуждения ГравиМот-1 основан на совершенно другом принципе работы, не имеющем ничего общего с ЦД. ...

Владимир Максимович, я вас хорошо понял. Несмотря на то, что Цд и Гр имеют разные принципы работы, их структурная геометрия имеет одну и ту же математическую основу. Разница только в природе сил и в их геометрической структуре. Однако, это не мешает нам использовать хорошее совпадение геометрии этих устройств в конкретных условиях поставленной задачи. Поэтому я использую математические наработки, сделанные на странице Комментарий_1. Естественно, что о центробежной силе нет разговора в этом варианте задачи. Рисунок в начале статьи я переделаю на более понятный и дополню анализ подробностями.

Проблема, описанная в пунктах 1 - 4 не вызывает у меня вопросов, мне понятны ваши разъяснения.

5. Фактически груз может двигаться только по касательной к окружности. Все другие движения заблокированы реакцией направляющей как опоры. Эта реакция возникает при любой попытке грузом пересечь красную линию. При вычислении момента этот факт надо учитывать, что толку использовать силу для ускорения груза в составе момента, если её часть заведомо погашена опорой. Поэтому надо использовать составляющую K, которая касательна к окружности. Она вычисляется из P. Сила T пересекает красную окружность и поэтому частично скомпенсирована направляющей. Это не значит, что составляющая, действующая на опору нам не нужна, просто она имеет отношение к движению груза вдоль спицы, так как именно из-за наличия красной направляющей возможно формальное движение груза вдоль спицы, это хорошо видно из системы отсчёта, связанной с осью привода. В этой задаче необходимо правильно разделить движение, на движение вдоль спицы и движение поперёк спицы, и при этом учесть реальную возможность совершать силой тяжести работу, понимая, что движение груза вдоль спицы есть по сути математический формализм, который вырождается когда мы переходим в систему отсчёта, которая связанна с центром красной направляющей.

Михаил 09.11.2010 г.

От 09.11.10

1.       Михаил, из Вашего письма обсуждению подлежит только последний абзац. И это замечательно!

          Из него следует, что для предварительной оценки схемы мотора на работоспособность, когда силами трения допустимо пренебречь, подтверждается ранее высказанное мною условие: «Таким образом, до тех пор, пока какие-то грузы могут падать по кольцевой направляющей, они будут понуждать к вращению «спицевый» диск».
          Если же из-за сил сопротивления (трение и кинематика) грузы падать не смогут, то, естественно, не будет и вращения диска.
          И при допущении, что силы трения и силы кинематического сопротивления пренебрежимо малы, можно оценить крутящий момент на выходном валу мотора именно для такого «идеализированного» варианта.

Силами трения мы пренебрегаем, так как они не имеют значения для анализа работы этого устройства. Момент на диске будет, но только, если расположение грузов не симметричное. Этот момент даст только переменную составляющую. Работа этого момента за полный оборот будет равна нулю. Если расположение грузов симметричное, то во всём диапазоне углов момент всегда равен нулю. Мы обязательно вычислим этот силовой момент и связанную с ним работу. Получить удобные аналитические выражения относительно оси привода, скорее всего, невозможно. Поэтому результат будет графический.

6. Использовать составляющую T нельзя, так как она частично погашена реакцией опоры груза. Все рассуждения на основе силы T принципиально неверны. ...

Михаил 10.11.2010 г.

От 11.11.10

          Михаил, мы опять обсуждаем с Вами только последний абзац Вашего письма. И это действительно замечательно!
          Будет или НЕ будет суммарная работа груза равной нулю пока что требует обоснования. Я уже говорил, что интуитивно чувствую, что будет, но расчёты (мои) этому противоречат.
          Что же касается неправомочности использования компоненты Т для вычисления крутящего момента, приложенного к диску, то этот тезис мне тоже не кажется (пока) достаточно убедительным.
          Для меня очевидно, что умножение компоненты К на расстояние её до оси мотора нельзя считать крутящим моментом для диска. Просто по той причине, что это приводит к абсурду для позиций, в которых груз оказывается на оси Х.
          Факт стремления вектора Т пересечь красную линию, указывает лишь на то, что груз все равно не сможет сдвинуться в направлении стрелки Т. Ведь не удивляет же Вас, Михаил, что вектор силы тяжести Р тоже норовит пересечь красную направляющую. В этом случае Вы, не задумываясь, берёте от вектора Р компоненту К.
          А я точно так же, но предварительно подумав, для вычисления крутящего момента беру компоненту Т от вектора К.

Владимир Максимович, когда я беру от Р компоненту К, то ставлю задачу получить такие ортогональные (линейно независимые) компоненты, чтобы разделить их физические свойства. Обратите внимание, что в моём случае
Р = К_τ+ К_n и R₁ = R_τ+ R_r;

К_τ - этот вектор всегда касателен к окружности и без помехи может перемещать груз по направляющей.
К_n - всегда перпендикулярен к окружности и поэтому скомпенсирован реакцией со стороны направляющей окружности (это направление полностью заблокировано).

В вашем случае
Р = Т + Т_?. Вы совершенно забыли про Т_?. Каждая из этих компонент содержит как перпендикулярную, так и касательную составляющую относительно направляющей окружности и поэтому ни о каком разделении свойств не может быть разговора, фактически они равноправны. Я мог бы заменить выражение "принципиально неверны" на формулировку "подобный подход усложняет задачу", если бы в ваших рассуждениях принимала участие сила Т_?. Потеря силы Т_? автоматически означает потерю части работы силы Р. При моём подходе при вычислении работы, потерь нет.

Момент вычисляется через векторное произведение
M = Р×R₁ = (К_τ+ К_n)×(R_τ+ R_r) = К_τ×R_τ + К_τ×R_r + К_n×R_τ + К_n×R_r;

К_τ×R_τ = 0; К_n×R_r = 0, так как векторы сонаправлены и не дают момента, остаются только компоненты составленные из перпендикулярных векторов.

M = Р×R₁ = К_τ×R_r + К_n×R_τ, находим проекции.

M_z = К_τ·R_r + К_n·R_τ. Направление Z перпендикулярно рисунку. Это справедливо в том случае, если движение груза совершенно свободно, но так как перпендикулярное направление к окружности заблокировано, то К_n·R_τ= 0. И для момента остаётся только
M_z = К_τ·R_r. И абсурда в таком выборе нет, так как от компоненты нельзя ожидать полного набора свойств исходного вектора. Это только проекция! Это не противоречит правилам вычисления момента. ...

Михаил 11.11.2010 г.

Комментарии к Обращение-1

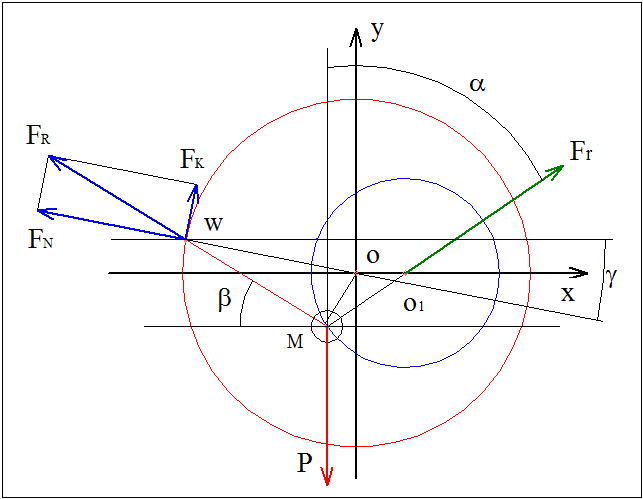
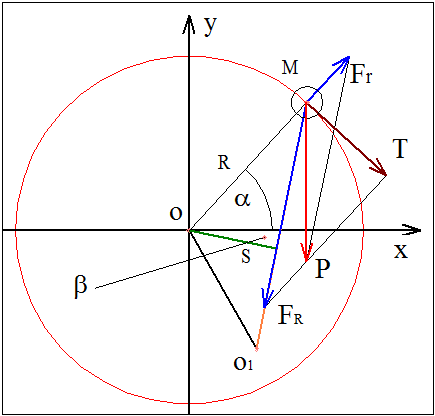
P – вес ролика.

F_R – сила реакции ротора на силу действующую вдоль серьги |MW| = L.

F_N – компонента от F_R нормальная к ротору (по направлению роторного радиуса).

F_k – компонента от F_R касательная к окружности ротора.

F_r – сила реакции направляющей ролика, направлена вдоль радиуса направляющей |MO₁| = r.

Пусть S – перпендикуляр из точки O к силе F_R; |OW| = R – радиус красной окружности. Тогда момент относительно точки O можно записать так,
M = -F_R·S = -F_k·R = -F_R·R·sin(β - γ) = ... (1)

... Но вот причина, по которой вместо непосредственной компоненты от вектора Р используется вектор реакции F_k, остаётся загадочной. ...

Использовать компоненту от вектора P вместо F_k от F_R невозможно, так как на серьгу действует не только сила P, но и сила F_r со стороны направляющей ролика, т. е. используя только проекцию от P, мы теряем проекцию от F_r. Если ось ротора застопорить, например для измерения момента, то будет выполнятся соотношение,
P + F_R + F_r = 0. (2) Это единственное соотношение, которое позволяет правильно вычислить силы, используя углы α, β, γ и найти момент по формуле
M = -F_R·R·sin(β - γ). Знак минус означает, что момент, действующий на ось ротора противоположен компенсирующему моменту со стороны стопора оси, который вычисляется из (1) без знака минус и (2).

В нижней точке P + F_r = 0, F_R = 0, т. е. реакция направляющей ролика полностью компенсирует вес ролика и момент в этом случае = 0. ...

22.09.2011 г.

Я и сейчас считаю, что ротор вращается не от действия реакции, вызванной воздействующей на ротор силой, а от действия самой воздействующей силы. В нашем случае такой воздействующей силой является некая компонента от вектора, отображающего вес груза.

У Вас в роли такой компоненты называется проекция вектора Р на линию серьги. (В данной Вашей методике рассматривается именно этот вариант).

Совсем не так! У меня F_R = -F_r - P, т. е. в общем случае F_R  ≠ -P_R.

Я в своём первом ответе показал (правда, без рисунка), что при Вашем варианте методика неизбежно уводит в нонсенс.

M = -F_R·S = -F_k·R = -F_R·R·sin(β - γ) = 0 в верхней и нижней точке и это можно доказать вычислениями. Нонсенс появляется только при неверном предположении, что F_R  = -P_R, но это совсем не так.

В данной конструкции существует только три реальные силы.
1. Сила от веса ролика P.
2. Сила вдоль серьги со стороны ротора F_R, которая мешает падать ролику.
3. Сила со стороны направляющей ролика F_r, которая тоже мешает падать ролику.

Если застопорить ротор (приложить компенсирующий момент чтобы ротор не вращался), то именно силы F_R и F_r будут обеспечивать ролику висячий покой.

Поэтому P + F_R + F_r = 0 при наличии стопора на роторе. Если убрать силу F_r, то ролик просто упадёт книзу. Пренебречь F_r невозможно! Как можно пренебречь силой, которая реально участвует в удержании ролика на весу???

23.09.2011 г.

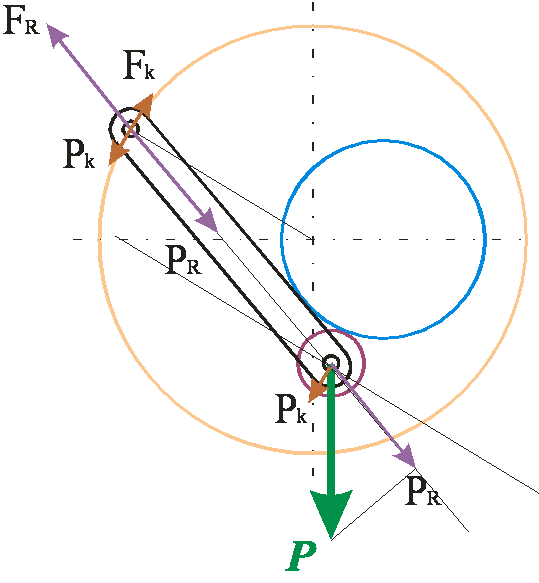
На рисунке 2 я показываю, что по правилам переноса сил векторы Р_R и Р_k можно разместить в точке подвеса серьги. Вместе с переносом силы положено добавлять компенсирующий вращающий момент. Но в нашем случае от переноса вектора Р_R компенсирующий момент вообще не возникает, так как направление исходного вектора точно проходит через точку подвески, а компенсирующий момент от переноса вектора Р_k никак не передаётся ротору, так как серьга подвешена свободно. По этой причине его тоже можно не показывать.
       В конечном счёте, можно записать и так:

-F_R = Р_R

-F_k = Р_k

M = -F_R·S = -F_k·R =Р_R·S = Р_k·R

       Вашему вектору F_r тут делать просто нечего! Наверное, потому, что связан он не с ротором, а с голубой направляющей. Да и на Вашей схеме этот вектор – не у дел. Впрочем, на данном этапе это тоже неважно. ...

Михаил, на рисунке 2 предыдущего моего письма я изобразил свой вариант построения векторов F_R и F_k. Вы считаете, что этот путь неверен.
       Прошу Вас показать теперь Ваш ход построения.

Владимир Максимович, мои построения следующие. Если застопорить ротор, то ролик будет висеть в состоянии покоя в любом выбранном вами положении. Состояние покоя указывает нам на то, что все силы скомпенсированы, т. е. сумма сил на ролике = 0. Мы знаем, что на ролик действует сила тяжести P. Вторая сила действует вдоль серьги и это F_R. Могут ли две силы в общем случае направленные под углом к друг другу дать нулевую результирующую? Нет! Ноль будет только в том случае, если они со направлены, а этого в общем случае нет. Поэтому в конструкции должна присутствовать еще одна сила, иначе мы не получим нуля, а он существует по факту опыта, при наличии стопора оси. И эта сила действует со стороны направляющей и обозначается F_r. Три силы P, F_R, F_r уже могут обеспечить равновесие. И это равновесие можно записать так,
P + F_R + F_r = 0

Если вместо стопора, подключить к оси, например генератор, то момент силы, действующий на ось генератора, при том же положении ролика, будет такой же, как и в случае стопора. Разница только в том, что ролик может двигаться с ускорением книзу и поэтому сила P будет несколько меньше на величину m·a, где a – ускорение вертикального падения ролика. Это ускорение меньше ускорения свободного падения, так как падать ролику мешает нагрузка от генератора. Вес ролика в случае движения конструкции равен,
P = m·(g - a), где g – ускорение свободного падения. При g = a, ролик будет в состоянии свободного падения, что возможно только при свободной оси ротора и нулевом весе элементов конструкции. Сила F_r перпендикулярна направляющей при условии, что ролик скользит по направляющей без трения, т. е. F_r направлена вдоль радиуса синей окружности, что и нарисовано на моей схеме. Фактически на этом и заканчивается физика и остаётся только формальная математика. ...

24.09.2011 г.

Для меня очевидно следующее (я просто вынужден снова повторяться, дабы не переходить с обсуждения Фомы на обсуждение Ерёмы):

1.    Любая сила реакции фигурирует только тогда, когда необходимо определить силу, удерживающую тело в неподвижном состоянии.
В нашем случае – это не так. В нашем случае тело как раз находится в подвижном состоянии, и требуется выбрать расчётную схему, позволяющую адекватно вычислить силу, приводящую его в такое состояние.

Владимир Максимович, силы реакции – есть следствие третьего закона Ньютона, а он выполняется независимо от состояния, подвижного или неподвижного. Подвижное состояние системы тел не отменяет законы взаимодействия по третьему закону Ньютона. Меняются только величины сил, входящие в уравнения, которые описывают данную конструкцию. Естественно это справедливо при условии, что система во время движения не меняет своего математического устройства. В нашем случае схема силового взаимодействия не меняется при наличии движения, не только при малых перемещениях, но и при любых больших, и поэтому расчётная схема не зависит от подвижности или неподвижности.

Но поскольку Вам, Михаил, по какой-то причине больше нравится работать с силами реакции, нежели с реально действующими силами, и поскольку Вы не смогли показать мне способ, применённый Вами для построения вектора F_R, я сам рассмотрю один из способов таких построений. ...

Силы реакции это и есть реальные силы, так как направлены со стороны тел, участвующих во взаимодействии по третьему закону. Со стороны ротора, ролика, направляющей.

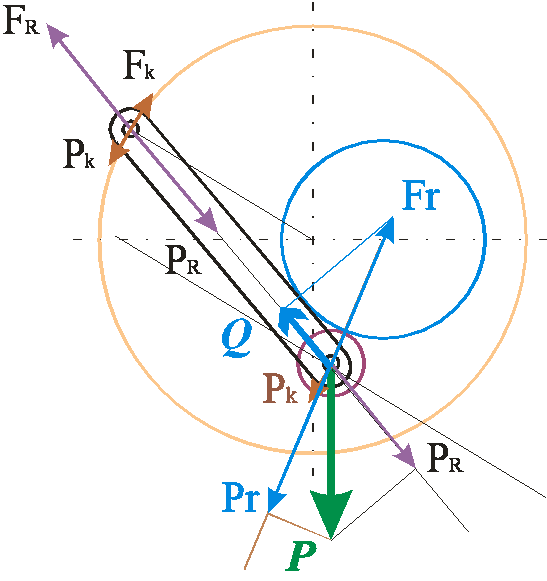
В основе предложенной Вами методики построения сил, лежит проекционный формализм не соответствующий законам Ньютона и ведущий к ошибкам. Почему? Ответ на этот вопрос сформулировать в простом и понятном виде сложно. Можно обсудить это вопрос.

Я очень извиняюсь, но вынужден отчасти повторится.

Определимся с реальными силами, т. е. силами, действующими по третьему закону Ньютона между телами. Взаимодействуют следующие тела: РОЛИК, НАПРАВЛЯЮЩАЯ, РОТОР. Направление сил рисуем относительно ролика.

1. P  – вес ролика. Эта сила направлена от ролика вертикально вниз. Модуль веса ролика равен
P = m·(g - a), где g – ускорение свободного падения; a – вертикальное ускорение ролика.

2. F_R – сила, действующая между ротором и роликом, через передаточное звено серьга. Эта сила направлена вдоль серьги. Модуль этой силы можно вычислить из векторного уравнения, которое строится из реальных сил в данной задаче или графически из схемы сил, построенной по правилу параллелограмма. Модуль этой силы нельзя определить через проекцию вектора P на направление вектора F_R.

3. F_r – сила, действующая между роликом и направляющей. Эта сила перпендикулярна направляющей, т. е. направлена по радиусу синей окружности. Модуль этой силы можно вычислить из векторного уравнения, которое строится из реальных сил в данной задаче или графически из схемы сил, построенной по правилу параллелограмма. Модуль этой силы нельзя определить через проекцию вектора P на направление вектора F_r.

Схема построения сил.

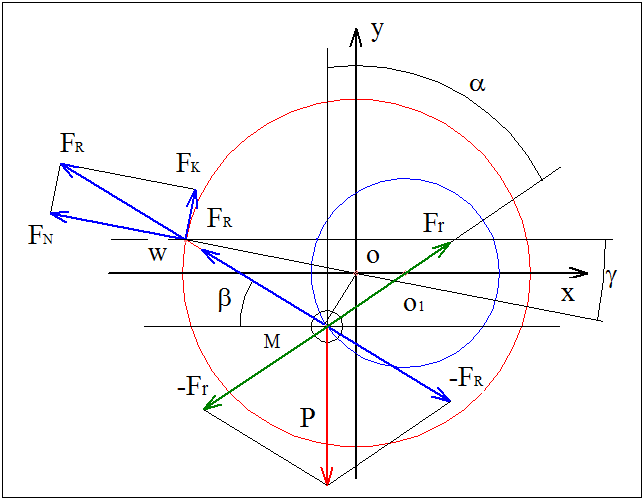
Это все реальные силы, действующие на ролик, обусловленные третьим законом Ньютона. Дополнительно для упрощения задачи будем считать, что серьга не имеют массы и трения в механизме нет. Построение сил на этом закончено.

Составляем векторное уравнение.
P + F_R + F_r = 0, т. е. F_R = -(P + F_r) – сила, действующая на ролик со стороны ротора через серьгу равна отрицательной сумме веса ролика и силы, действующей со стороны направляющей. По третьему закону ролик действует противоположной силой на ротор равной -F_R = P + F_r.

На этом заканчивается физика и остаётся только формальная математика.

Проецируем векторное уравнение на оси x и y.
-F_Rx + F_rx = 0, так как P_x = 0. (1)

-P + F_Ry + F_ry = 0, так как P_y = P – модуль веса ролика. (2)

F_Rx= F_R·cos(β);   F_rx = F_r·sin(α);   F_Ry = F_R·sin(β);   F_ry= F_r·cos(α).

Из (1) имеем F_R·cos(β) = F_r·sin(α). (3)

Из (2) имеем -P + F_R·sin(β) + F_r·cos(α) = 0. (4)

Подставляем (3) в (4).

-P + F_R·sin(β) + F_R·cos(β)·cos(α)/sin(α) = 0;

-P + F_R·sin(β) + F_R·cos(β)·ctg(α) = 0;

P = F_R·(sin(β) + cos(β)·ctg(α));

F_R = P/(sin(β) + cos(β)·ctg(α)).

M = F_R·R·sin(β - γ) = P·R·sin(β - γ)/(sin(β) + cos(β)·сtg(α))

Так как S = R·sin(β - γ) и r·cos(α) = S·cos(β), то

M = P·r·cos(α)/(sin(β) + cos(β)·ctg(α))/cos(β);

M = P·r·cos(α)/(sin(β)·cos(β) + cos(β)²·ctg(α));

M = P·r·sin(α)/(sin(β)·cos(β)·tg(α) + cos(β)²).

S·sin(β) + e = r·sin(α);   S·sin(β) = r·sin(α) - e, где e – расстояние между центрами синей и красной окружности по оси x.

tg(β) = S·sin(β)/S·cos(β) = (r·sin(α) - e)/(r·cos(α)) = (sin(α) - e/r)/cos(α) = tg(α) - w/cos(α), где w = e/r.

tg(β) = tg(α) - w/cos(α) = tg(α)·(1 - w/sin(α)).

sin(β)·cos(β) = tg(β)/(1 + tg(β)²) (формула из справочника)

cos(β)² = 1/(1 + tg(β)²) (формула из справочника)

M = P·r·sin(α)/(tg(β)·tg(α)/(1 + tg(β)²) + 1/(1 + tg(β)²));

M = P·r·sin(α)·(1 + tg(β)²)/(1 + tg(β)·tg(α));

M = P·r·sin(α)·(1 + tg(α)²·(1 - w/sin(α))²)/(1 + tg(α)²·(1 - w/sin(α)));

M = P·r·sin(α)·(1 + (sin(α) - w)²/cos(α)²)/(1 + tg(α)·(sin(α) - w)/cos(α));

M = P·r·sin(α)·(cos(α)² + (sin(α) - w)²)/(cos(α)² + sin(α)·(sin(α) - w));

M = P·r·sin(α)·(cos(α)² + (sin(α) - w)²)/(1 - w·sin(α));

M = P·r·sin(α)·(1 + w² - 2·w·sin(α))/(1 - w·sin(α));

При α = 0, 180°, т. е. когда груз находится в верхней и нижней позиции M = 0.

Дополнительно L·sin(β) = r·cos(α) + R·sin(γ), где L – длина серьги. ...

06.10.2011 г.

Из ранее написанного следует, что момент относительно точки O с точностью до знака равен M = F_R·S, где сила F_R направлена вдоль кулисы. Очевидно, что длина кулисы не может влиять на передачу величины силы вдоль кулисы.

Рычаг S перпендикулярен кулисе и поэтому зависит только от её угловой ориентации. Длину кулисы можно менять притом же угле β без изменения S при этом будет меняться и R.

Таким образом единственным параметром влияющим на величину момента является угловое положение кулисы, т. е. зависимость от угла β. Докажем, что и это не влияет на момент. Из ранее написанного следует
S·cos(β) = r·cos(α);

S·sin(β) = r·sin(α) - e.

Возводим эти выражения в квадрат
S²·cos(β)² = r²·cos(α)²;

S²·sin(β)² = r²·sin(α)² + e² - 2·e·r·sin(α).

Суммируем эти уравнения
S²·cos(β)² + S²·sin(β)² = r²·cos(α)² + r²·sin(α)² + e² - 2·e·r·sin(α);

S² = r² + e² - 2·e·r·sin(α).

Таким образом, рычаг S не зависит от угла β, т. е. от угловой ориентации кулисы.

Обратите внимание, что
(S/r)² = 1 + w² - 2·w·sin(α), т. е. это выражение, которое стоит в числителе формулы момента.

M = F_R·r·√(1 + w² - 2·w·sin(α));

07.10.2011 г.

...

3.    На приведённом ниже рисунке я представляю себе следующий принцип формирования  момента вращения ротора от падающего груза с массой, отображаемой на рисунке вектором Р.
       Груз подвешен на двух нитках. Свободный конец одной из них закреплён на ободе ротора. Свободный конец другой нитки закреплён на неподвижной станине.

Да, задача сводится к этой схеме, груза подвешенного на двух нитях. В этом случае хорошо видно, что силы суммируются по правилу параллелограмма.

       Я думаю, что от вектора Р следует взять компоненту Т, касательную к траектории груза в мгновенной точке его нахождения. Далее, в соответствии с правилами теоретической механики, найденную компоненту следует перенести в точку подвески. В соответствии с теми же правилами вместе с переносом силы полагается показать и компенсирующий момент, удерживающий серьгу в первоначальном (до переноса силы) положении. Я этого не делаю, так как считаю, что при отсутствии жёсткого задела на концах серьги этот компенсирующий момент всё равно никак не влияет на величину момента вращения.

Да, компоненту T можно использовать в этой задаче в качестве реальной силы. Момент относительно точки O₁ (на моём рисунке) в этом случае будет равен M_o1 = T·r.

       Я считаю, что именно компонента Т, проходящая через точку подвески и помноженная на расстояние до компоненты от оси ротора, как раз и формирует искомый момент вращения.

Да, если считать точкой подвеса центр масс ролика и для вычисления действующего рычага из точки O опустить перпендикуляр к компоненте T, то всё будет правильно. Можно доказать, что в этом случае момент будет равен
M_o = P·r·sin(α)·(1 + w² - 2·w·sin(α))/(1 - w·sin(α)).

Обратите внимание, что в такой постановке задачи, ротор можно заменить сплошным диском с осью вращения O₁ на котором просто крепится груз (ролик), при измерении момента относительно точки O, т. е. измеритель приложен к контуру ротора и перпендикулярен R. Формальная математическая независимость момента от параметров кулисы и выражается в такой практической возможности. Здесь аналогия, например, с колесом, спицы в котором можно сделать любой формы и положения и в любом количестве. При w = 0 задача вырождается в задачу о колесе на плоскости с произвольно закреплённым грузом. В нашем случае это аналог задачи о колесе, катящемся на вертикально подвижной плоскости с эксцентриситетом и закреплённым на нём грузом. Например, вращающийся эксцентрик, толкающий шток. В этом случае момент на его ободе, связанный со смещением центра масс эксцентрика и будет соответствовать рассматриваемой задаче.

...

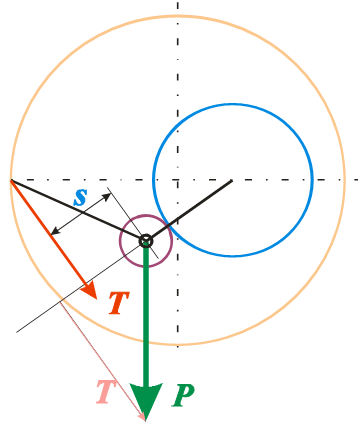
2.    Груз может оказывать усилие на ротор только через левую (на моём рисунке) нить. Усилие, побуждающее ротор к вращению, передаётся непосредственно в точку подвески. Никаких других точек контакта груза с ротором не существует. Следовательно, и рассмотрению может подлежать только та сила, которая приложена к ротору в точке подвески. На моём рисунке эта сила обозначена вектором Т. Другие силы к ротору не прикладываются (трением на данном этапе – пренебрегаем).

3.    Специально подчёркиваю, что центр массы ролика не является точкой подвески, через которую ролик контактирует с ротором.

Если мы признаем силу T реальной (в данной задаче это формально возможно), то должны указать со стороны какого тела она действует. В данном случае она действует со стороны ролика и неважно как она передаётся ротору по третьему закону. Эта сила имеет рычаг относительно центра O и она приложена к ролику и это главное. Если перенести реальную силу, приложенную к телу в другое место, то это приведёт к необоснованному изменению рычага и соответственно момента. Сила T появляется как составляющая силы P, которая приложена к ролику и поэтому составляющая T не может исходить из другой точки. Указанное Вами положение силы T, приводит к появлению в задаче дополнительного момента и требует компенсации. Таких искусственных ситуаций лучше избегать.

08.10.2011 г.

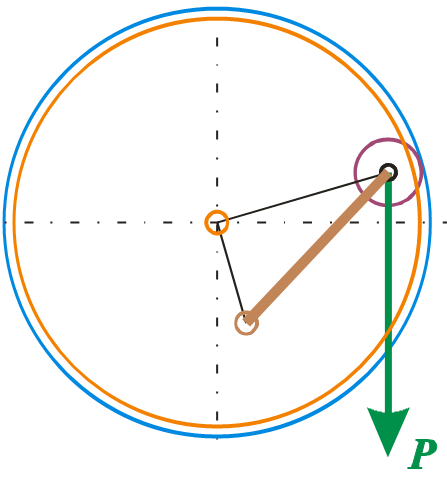
В этом случае всё просто. Момент равен силе, касательной к окружности, умноженной на радиус движения, т. е.
M_R = T·R = P·R·cos(α), где α – угол между радиусом ролика и горизонтальной осью x и

T = P·cos(α).

Михаил, у меня в проекте имеются существенно важные детали, на которые Вы, почему-то, не посчитали нужным обратить внимание.

В этом случае имеет значение только траектория, по которой движется ролик. Момент можно записать и по-другому, но это будет тоже самое.

M_R = F_R·S = P·X, где X – проекция радиуса R на ось x.

X = R·cos(α), тогда P·X = P·R·cos(α) = T·R.

Так как F_R·cos(α + β) = T; R·cos(α + β) = S, то

F_R·S = T/cos(α + β)·S = T/cos(α + β)·R·cos(α + β) = T·R.

13.10.2011 г.

...

3.    Тогда, при Вашем подходе, получается, что положение точки подвески вообще не имеет значения.
       На этот случай я «припас» для Вас специальную задачку (рисунок 3).

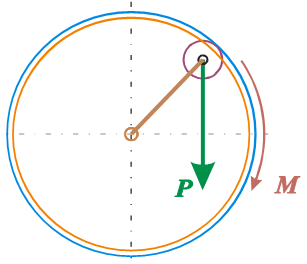
Рис. 3

По этой схеме ролик-груз катается всё по той же направляющей, но ось подвески совпадает с осью ротора.

4.    Что мешает ролику-грузу свободно «вертануться» вокруг оси своей подвески, совпадающей с осью ротора?
       Я думаю, что Ваш ответ будет однозначным: «Ничего!»
       А тогда, какой момент вращения будет создаваться на роторе при свободном падении груза?
       И тут – ситуация!
       С одной стороны – Вы понимаете, что момент не создаётся. Но с другой стороны – как, «честный мужчина», Вы обязаны будете «жениться», так как именно Вы обозначили, что
М = Т·R. И что имеет значение только траектория, по которой движется ролик.

Формула М = Т·R и в этом случае правильна. Проблема в том, что действующий вес ролика зависит от его вертикального ускорения и сила Т соответственно тоже зависит. Ранее это было записано в виде
P = m·(g - a_y) – зависимость веса ролика от вертикального ускорения. При g = a_y невесомость. Состояние невесомости достигается только при строго вертикальном падении, когда не мешает направляющая, т. е. не в нашем случае. Найдем силу Т.
Т = P·cos(α) = m·(g - a_y)·cos(α) = m·(g·cos(α) - a_τ) или

Т = m·(a_0τ - a_τ) = m·(g·cos(α) - R·dω/dt), где dω/dt – угловое ускорение ролика; a_0τ – касательная составляющая ускорения свободного падения; a_τ = R·dω/dt – касательное ускорение ролика.

В случае свободного падения ролика мы имеем задачу о движение тела по наклонной криволинейной поверхности под действием собственного веса. В этом случае касательное ускорение ролика равно
a_0τ = g·cos(α). Это следует, например, из

m·v²/2 = g·m·h. Кинетическая энергия ролика равна работе по перемещению ролика в поле тяжести, где h – высота падения; v – скорость касательная к траектории ролика. Дифференцируем это выражение
m·v·a_0τ = g·m·v_y;              v_y = v·cos(α).

m·v·a_0τ = g·m·v·cos(α);      a_0τ = g·cos(α).

Момент можно записать так
М = Т·R = m·(g·cos(α) - R·dω/dt)·R. Фактически мы записали дифференциальное уравнение из которого можно определить все параметры движения, например угловую скорость ω.

dω/dt - g/R·cos(α) = -М/(m·R²) = -М/I, где I – момент инерции. Из случая свободного падения ролика при М = 0, можно получить общее решение этого дифференциального уравнения.

dω/dt - g/R·cos(α) = 0 или d²φ/dt² + g/R·sin(φ) = 0. Это уравнение колебаний маятника, что соответствует предложенной Вами задаче, где φ – угол отклонения маятника от положения равновесия φ = 90° - α; ω = dα/dt.

В случае малых колебаний около положения равновесия это уравнение записывают и так
d²φ/dt² + g/R·φ = 0;       d²φ/dt² + ω₀²·φ = 0;     ω₀  = √(g/R) – угловая частота колебаний маятника.

С уважением, Михаил.

15.10.2011 г.

Оглавление

Продолжение

Назад

Главная страница