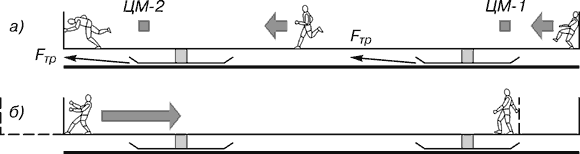
В будущем программа моделирования виброхода будет выложена в приложении.
Однако прежде чем вплотную заняться этой моделью, определится со следующими моментами.
1. Исследуем особенности движения виброхода с классической позиции.
2. Выберем параметры модели.
3. Исследуем доступные экспериментальные данные.
4. Оценим роль трения.
5. Поговорим об особенностях движения механизма в режиме старт-стоп.

Что такое виброход с классической позиции можно прочитать у Н. В. Гулиа.

Нурбей Владимирович Гулиа.
Российский учёный и изобретатель в области маховичных накопителей энергии, бесступенчатого механического привода, гибридных транспортных силовых агрегатов; популяризатор науки и техники.

Цитируем из книги «Инерция» (1982 г.)

«Теперь мы вплотную подошли, пожалуй, к самому распространенному заблуждению, связанному с инерцией, – к инерцоидам, которые с полным основанием можно назвать инерционными химерами» ст. 144.

«Как движется инерцоид, хорошо иллюстрирует следующий опыт. Если стать на санки, взять в руки молот и бить им по заднему краю санок, то они толчками поедут вперед (в случае с колесной тележкой молот при ударе нужном разгонять «помягче»). Если в этом опыте человека заменить механизмом, получится инерцоид. Действие механизмов самых различных инерцоидов, как бы сложны они ни были, сводятся к одному — созданию резкого импульса, кратковременного, но с развитием большой силы, в одну сторону, и мягкого импульса, длительного, но с развитием малой силы,— в другую. Согласно законам механики, внутренними силами машины невозможно создать импульс (приближенно импульс — произведение силы на длительность её действия), который в одну сторону больше, чем в другую. Сумма импульсов в обе стороны равна нулю, т. е. машина, как бы сложна она ни была, одними внутренними силами никуда не сдвинется. Но хитрость здесь в другом. Так как импульс можно «растянуть» как угодно сильно (например, разгоняя молоток для удара целый час), силу, направленную в сторону этого импульса, можно сделать как угодно малой. И как бы ни было мало сопротивление движению тележки с инерцоидом на нем, силу эту можно сделать ещё меньше. Тогда тележка из-за трения не сдвинется в сторону этого импульса. Когда же молот ударит по тележке, импульс будет очень кратковременным — доли секунды, сила же — очень велика и преодолеет силу трения, какой бы большой та ни была. Отсюда и движение тележки с инерцоидом в сторону большей силы (что и демонстрируется обычно создателями инерцоидов)». ст. 148.

«Инерцоиды, описанные в книге В. Н. Толчина, отличаются только тем, что в них удары наносятся без остановки груза. Груз, двигаясь по окружности, ударяет по тормозу и проскакивает, имея, конечно, после такого удара весьма малую скорость. Далее груз опять разгоняется и снова встречается с тормозом. Разницы в принципе действия инерцоида тут нет» ст. 149.

Правда об инерцоидах

«Проще представить себе не машину, а самих себя, поэтому пусть корпусом инерцоида будет служить длинная тележка на опорах с очень малым трением (коньки на льду!), а грузом – непосредственно мы сами (рис. 3). Медленно и осторожно разбегаемся (а), набираем скорость, и вот мы уже у передней стенки тележки. Она не двинулась, так как ускорение наше слишком мало, касательная сила ног на пол слабая, и сила трения коньков о лед, как бы ничтожна ни была, удержала ее от движения назад. И все же эта сила трения двинула наш инерцоид, хотя корпус и неподвижен. Ведь общий центр масс системы «груз (человек) – корпус» переместился с положения ЦМ-1 в положение ЦМ-2. Вот оно, истинное движение инерцоида. И движение это – благодаря внешней силе трения Fтр, направленной со стороны льда на коньки именно вперед, по движению центра масс!

Рис. 3. Опыт, разъясняющий причину движения инерцоида

Далее следует наш энергичный бросок с набранной скоростью на стенку и отталкивание от нее руками (б). Корпус резко сдвигается вперед – мы назад, сила трения коньков о лед преодолена. Вот оно, кажущееся движение инерцоида. На самом же деле центр масс в этом случае практически остался на месте – импульс внешней силы трения за короткое время удара очень мал. Тележка сдвинулась вперед, мы назад, а центр масс остался на месте. Если при этом толчке и отбросе назад мы оказались уже у задней стенки – хорошо, начнем разбег сначала. Если нет – отойдем назад, сместив центр масс немного назад (опять благодаря силе трения!), а затем повторим первое движение – плавный разгон. Истинное движение инерцоида, оказывается, происходит совсем не тогда, когда перемещается корпус, и как у всех наземных средств транспорта зависит только от внешней силы.»

Из сказанного Н. В. Гулиа можно выделить следующий предельный случай движения виброхода, когда в быстром полутакте центр масс не перемещается, а в медленном при отсутствии перемещения корпуса, он сдвигается на величину пробега человека по тележке с коэффициентом равным относительной массе человека в тележке. Это режим старт-стоп без разгона. Поясним это следующими расчётами:
\( \displaystyle m_1 \cdot s_1 = m_2 \cdot s_2 - \) условие равновесия относительно центра масс, где m₂ – масса человека;
m₁ – масса тележки; \( \displaystyle s_2 + s_1 = s - \) база перемещения по тележке.
\( \displaystyle s_2 = \frac{m_1 \cdot s }{m_2 + m_1} - \) перемещение человека относительно опоры при движении человека по ней от 0 до s, если нет трения.

\( \displaystyle s_1 = \frac{m_2 \cdot s }{m_2 + m_1} = B - \) перемещение тележки относительно опоры при движении человека по ней от 0 до s, если нет трения.
Перемещение центра масс тележки s_м относительно опоры при движении человека по ней от 0 до s, при условии, что трение не позволило сдвинуть тележку с места будет тоже равно s₁. В промежуточном случае перемещение распределяется между тележкой и центром масс и в сумме равно s₁. Взаимосвязь между этими перемещениями будет, s₁ - s_т = s_м или s₁ = s_м + s_т.

Это свойство позволяет оценить перемещение центра масс при измерении величины перемещения тележки относительно заданной фазы механизма в периодическом движении.

Оценим скоростные возможности этой предельной модели. Полагаем, что быстрый возврат человека происходит за очень малое время t → 0, соответственно мы гарантируем очень маленький импульс за время быстрого возврата и можем им пренебречь.

Чтобы обеспечить отсутствие разгона виброхода мы должны предположить, что человек половину пути разгоняется, а половину тормозится, не превышая силы трения, так чтобы к концу пути иметь нулевую скорость, в противном случае будет избыточный импульс.

\( \displaystyle \frac{1}{2} \frac{F_{тр}}{m_2} \cdot t^2 = \frac{s}{2} - \) перемещение при равноускоренном движении, половина пути разгон.

\( \displaystyle \frac{F_{тр}}{m_2} \cdot t^2 = s \);

\( \displaystyle T = 2 \sqrt{ \frac{m_2 \cdot s }{F_{тр}} } \);

\( \displaystyle v = \frac{B}{2} \sqrt{ \frac{F_{тр}}{m_2 \cdot s} } \), где F_тр – сила трения; t – половина периода, разгона или торможения; T – тактовый период (разгон-торможение - быстрый отход назад); v – средняя скорость перемещения центра масс.

Сделаем числовые оценки по этой формуле с параметрами инерцоида Толчина. В частном случае, для пружинного инерцоида В. Н. Толчина, формулу параметра "B" надо интерпретировать в виде: B = 2·R·m₂/(m₂ + m₁). При m₂ = 2·0,13 = 0,26 кг; m₁ = 0,69 кг; R = 60 мм. При s = 2·R = D =120 мм; B = 32,84 мм – номинальная амплитуда. Именно на эту величину в классическом варианте при каждом полуобороте должен перемещается корпус центробежного вибратора с указанными параметрами при отсутствии силы трения в колёсах.

При F_тр = 1 грамм;    v = 9,20 мм/с,   время такта Т = 3,57 сек;   μ_об = 0,0010; μ_ос = 0,021.

При F_тр = 6 грамм;    v = 22,55 мм/с, время такта Т = 1,46 сек;   μ_об = 0,0063; μ_ос = 0,126.

При F_тр = 25 грамм;  v = 46,03 мм/с, время такта Т = 0,713 сек;  μ_об = 0,0263; μ_ос = 0,526.

При F_тр = 100 грамм; v = 92,06 мм/с, время такта Т = 0,357 сек; μ_об = 0,1053; μ_ос = 2,105.

Где μ_об – коэффициент трения, приведённый к ободу колеса; μ_ос – коэффициент трения, приведённый к оси колеса. μ_ос = (D_обода/D_оси)·μ_об, где D_обода – диаметр колеса; D_оси – диаметр оси.
Для пружинного инерцоида по чертежу колеса D_обода = 30 мм; D_оси = 1,5 мм. Значение μ_ос = 2,105 при F_тр = 100 грамм выходит за пределы реальных сил трения, так как больше веса прибора.

Обратите внимание, что характер движения грузов инерцоида приблизительно соответствует нашей предельной модели. Скорость грузов в проекции на направление движения возрастает от нуля до максимума и снова спадает до нуля. При этом сила, действующая на корпус меняется по более сложному закону и может превышать силу трения на некоторой части траектории грузов. При этом мы должны понимать, что реальном инерцоиде обратный импульс не равен нулю и, как правило, происходит откат корпуса назад в отличие от этой модели. Все это снижает скорость. Поэтому эти оценки для модели в режиме старт-стоп (центр масс периодически останавливается) максимальны. Можно конечно взять трение ещё больше, однако это уже выходит за разумные пределы, так как эксперименты на качелях при трении в 25 грамм уже становятся невозможными, вибрация нарушает движение. Таких вибраций в реальном опыте Толчина не было. Обратите внимание, что скорость "человека" в середине пути максимальна, она в два раза больше средней. Рассмотрим для сравнения данные эксперимента из книги Толчина.

«Однотактный инерцоид с пружинным заводом».

Он имеет следующие параметры:

Общий вес инерцоида с кожухом – 0,95 кг (950 грамм);

Ход вперед – 0,09 м (90 мм);

Ход назад – 0,03 м (30 мм);

Трение в колесах при движении – менее 0,006 кг (6 грамм).

Трение из неподвижного состояния 25 г.

Результирующий ход за цикл – 90 мм - 30 мм = 60 мм.

В тексте приводится описание следующего опыта:

«Поперек дорожки наклеить две полоски бумаги на расстоянии 500 мм друг от друга. Запустить инерцоид по дорожке от одной полоски до другой, замерив время пробега этого расстояния по секундомеру. При трении в колесах 25 г, измеренном из неподвижного состояния, инерцоид проходит это расстояние за 2,0–2,5 c. При каждом такте он сначала продвигается вперед на 90 мм, а затем отступает назад на 30 мм».

Найдем количество тактов: 500 мм/60 мм = 8,33. Найдем тактовый период, он находится в диапазоне от 2,0/8,33 до 2,5/8,33, т. е. 0,24–0,30 сек средняя частота соответственно (4,2–3,3 Гц). Соответственно медленный полутакт протекает за несколько меньшее время. При такой настройке трение в колёсах влияет на колебания механизма очень незначительно. Средняя скорость инерцоида 250–200 мм/сек.

Скорость движения практически зависит только от частоты работы механизма, например инерцоид с тактовым периодом 1 сек, имеет скорость 60 мм/сек. Чтобы найти скорость движения пружинного инерцоида надо частоту тактового периода умножить на 60. Инерцоид вне дополнительной тележки движется эффективнее. Величины отката назад и хода вперед измеряются по отношению к корпусу относительно поверхности земли. Дополнительная тележка движется под ударами инерцоида с его средней скоростью.

Вывод из сравнения очевидный. Предельная модель не соответствует реальному движению инерцоида. В дальнейшем рассмотрим вариант, когда виброход имеет возможность разгоняться, но для этого первоначально оценим роль трения.

Вперёд

Назад