Механика инерцоида
     Главная | Силы Кориолиса_1 | Мой профиль | Выход Вы вошли как Гость | Группа " Гости" | RSS
Механика инерцоида

Выше

Закон вращения в не ИСО
\(~~~~~~~\) rx =  Rx·cos(Ω·t) + Ry·sin(Ω·t);

\(~~~~~~\) ry = -Rx·sin(Ω·t) + Ry·cos(Ω·t).

\(~~~~~~\) rx = -a·sin(ω·t)·cos(Ω·t) + b·cos(ω·t)·sin(Ω·t);

\(~~~~~~\) ry =  a·sin(ω·t)·sin(Ω·t)  + b·cos(ω·t)·cos(Ω·t), где

a — основная амплитуда раскачивания маятника, обусловленная его отклонением от положения равновесия при пуске (большая полуось эллипса в инерциальной системе отсчёта); ω — угловая частота маятника; Ω — угловая скорость вращения земли; b — отклонение маятника, связанное с вращением земли (малая полуось эллипса в инерциальной системе отсчёта).

Дифференцируем и получаем скорости
vx = -a·ω·cos(ω·t)·cos(Ω·t) + a·Ω·sin(ω·t)·sin(Ω·t)  - b·ω·sin(ω·t)·sin(Ω·t) + b·Ω·cos(ω·t)·cos(Ω·t);

vy =  a·ω·cos(ω·t)·sin(Ω·t)  + a·Ω·sin(ω·t)·cos(Ω·t) - b·ω·sin(ω·t)·cos(Ω·t) - b·Ω·cos(ω·t)·sin(Ω·t).

\(~~~~~~\) vx =   Ω·ry  - a·ω·cos(ω·t)·cos(Ω·t) - b·ω·sin(ω·t)·sin(Ω·t);

\(~~~~~~\) vy =  -Ω·rx + a·ω·cos(ω·t)·sin(Ω·t)  - b·ω·sin(ω·t)·cos(Ω·t).

\(~~~~~~~~~~~~\) vx =   Ω·ry  + Vx·cos(Ω·t) + Vy·sin(Ω·t);

\(~~~~~~~~~~~~\) vy =  -Ω·rx  - Vx·sin(Ω·t)  + Vy·cos(Ω·t), что сводится к векторному уравнению

v = -[Ω×r] + vr. Форма уравнения для вектора скорости не зависит от рассматриваемой задачи. Однако, в этом случае, слагаемые ортогональны только при колебаниях маятника в одной плоскости.

Дифференцируем и получаем ускорения
ax =  a·ω2·sin(ω·t)·cos(Ω·t) + a·ω·Ω·cos(ω·t)·sin(Ω·t) + a·Ω·ω·cos(ω·t)·sin(Ω·t) + a·Ω2·sin(ω·t)·cos(Ω·t) - b·ω2·cos(ω·t)·sin(Ω·t) -

- b·ω·Ω·sin(ω·t)·cos(Ω·t) - b·Ω·ω·sin(ω·t)·cos(Ω·t) - b·Ω2·cos(ω·t)·sin(Ω·t);

ay = -a·ω2·sin(ω·t)·sin(Ω·t) + a·ω·Ω·cos(ω·t)·cos(Ω·t) + a·Ω·ω·cos(ω·t)·cos(Ω·t) - a·Ω2·sin(ω·t)·sin(Ω·t) - b·ω2·cos(ω·t)·cos(Ω·t) +

+ b·ω·Ω·sin(ω·t)·sin(Ω·t) + b·Ω·ω·sin(ω·t)·sin(Ω·t) - b·Ω2·cos(ω·t)·cos(Ω·t).

Приводим через преобразования к виду (3)
ax = -ω2·rx + a·ω·Ω·cos(ω·t)·sin(Ω·t) + a·Ω·ω·cos(ω·t)·sin(Ω·t) + a·Ω2·sin(ω·t)·cos(Ω·t) - b·ω·Ω·sin(ω·t)·cos(Ω·t) - b·Ω·ω·sin(ω·t)·cos(Ω·t) - b·Ω2·cos(ω·t)·sin(Ω·t);

ay = -ω2·ry + a·ω·Ω·cos(ω·t)·cos(Ω·t) + a·Ω·ω·cos(ω·t)·cos(Ω·t) - a·Ω2·sin(ω·t)·sin(Ω·t) + b·ω·Ω·sin(ω·t)·sin(Ω·t) + b·Ω·ω·sin(ω·t)·sin(Ω·t) - b·Ω2·cos(ω·t)·cos(Ω·t).


ax = -ω2·rx + 2·a·ω·Ω·cos(ω·t)·sin(Ω·t) + 2·a·Ω2·sin(ω·t)·cos(Ω·t) - 2·b·ω·Ω·sin(ω·t)·cos(Ω·t) - 2·b·Ω2·cos(ω·t)·sin(Ω·t) - a·Ω2·sin(ω·t)·cos(Ω·t) + b·Ω2·cos(ω·t)·sin(Ω·t);

ay = -ω2·ry + 2·a·ω·Ω·cos(ω·t)·cos(Ω·t) - 2·a·Ω2·sin(ω·t)·sin(Ω·t) + 2·b·ω·Ω·sin(ω·t)·sin(Ω·t) - 2·b·Ω2·cos(ω·t)·cos(Ω·t) + a·Ω2·sin(ω·t)·sin(Ω·t) + b·Ω2·cos(ω·t)·cos(Ω·t).


ax = -ω2·rx + 2·a·ω·Ω·cos(ω·t)·sin(Ω·t) + 2·a·Ω2·sin(ω·t)·cos(Ω·t) - 2·b·ω·Ω·sin(ω·t)·cos(Ω·t) - 2·b·Ω2·cos(ω·t)·sin(Ω·t) + Ω2·rx;

ay = -ω2·ry + 2·a·ω·Ω·cos(ω·t)·cos(Ω·t) - 2·a·Ω2·sin(ω·t)·sin(Ω·t) + 2·b·ω·Ω·sin(ω·t)·sin(Ω·t) - 2·b·Ω2·cos(ω·t)·cos(Ω·t) + Ω2·ry.

Получили дифференциальные уравнения
ax = -ω2·rx + 2·Ω·vy + Ω2·rx;

ay = -ω2·ry - 2·Ω·vx + Ω2·ry, так как

-ω2·r = -i·ω2·rx - j·ω2·ry;

[Ω×v] = k·Ω·(i·vx + j·vy) = k·i·Ω·vx + k·j·Ω·vy = j·Ω·vx - i·Ω·vy (правый винт);

Ω2·r = i·Ω2·rx + j·Ω2·ry, получим (3).

Исследование уравнения (3) показывает, что при условии ω·b = Ω·a, соблюдается уравнение (-ω2·r - [Ω×v] + Ω2·r)·[Ω×v] = 0, т. е. скалярное произведение равно нулю, а значит, множимые вектора ортогональны.
Равенство ω·b = Ω·a, соответствует начальным условиям пуска, когда маятник в неинерциальной системе, отклоняется на некоторый угол и отпускается без толчка, что изображено на рис. 111 у Арнольда (условие покоя в не ИСО в момент старта). Равенство ω·b = Ω·a, эквивалентно, начальным условиям пуска маятника в рассматриваемом примере. Анализ этой ситуации показывает, что уравнение движения маятника в этом случае можно записать в виде
a = aτ - [Ω×v] (4), где aτ — касательное ускорение маятника (тангенциальное); -[Ω×v] — вращательное ускорение вектора скорости. Эта форма записи уравнения физически обусловлена. Она показывает, что маятник движется поступательно с ускорением aτ, которое является причиной изменения его энергии, а вектор скорости маятника совершает гироскопическое движение без изменения энергии по закону -[Ω×v]. По этой причине пренебрежение членом Ω2·r, является серьёзной теоретической ошибкой, так как исключает возможность преобразования к физически обоснованному виду (4), без использования надуманной силы Кориолиса.

Уравнение (4) просто интегрируется по времени и позволяет правильно ответить на вопрос, поставленный в начале статьи, какая относительная скорость вращения маятника относительно земли?
dv = a·dt = aτ·dt - [Ω×v]·dt = aτ·dt - [Ω×dr];

v = ∫ aτ·dt - ∫[Ω×dr] = vr - [Ω×r].

Рассмотрим уравнение (3) при условии ω·b ≠ Ω·a. В этом случае скалярное произведение (-ω2·r - [Ω×v] + Ω2·r)·[Ω×v] = const. Обозначим as = -ω2·r - [Ω×v] + Ω2·r.
as0·[Ω×v0] = as·[Ω×v] = const;

Ω·[v0×as0] = Ω·[v×as] = const;

[v0×as0] = [v×as] = P = const — вектор имеет направление угловой скорости. P — можно назвать гироскопической мощностью на единицу массы.

С выражением [v×as] можно связать угловую скорость, разделив его на квадрат скорости
Ωs = [v×as]/v2 = [v0×as0]/v2 = P/v2.

В этом случае можно записать уравнение
a = aτ + [Ωs×v] - [Ω×v] (5), где [Ωs×v] — центростремительное ускорение в не ИСО. При ω·b = Ω·a, Ωs = 0. При Ω = 0 будет стандартное разложение на тангенциальное и нормальное ускорение в ИСО.

Маятник в не ИСО движется под действием трех физически обусловленных ускорений:
\(~~~~~~~~\) aτ — тангенциальное ускорение маятника в не ИСО, порождённое взаимодействием с потенциальным полем гравитации;

 [Ωs×v] — центростремительное ускорение маятника в не ИСО, порождённое взаимодействием с потенциальным полем гравитации и влиянием неинерциальной системы отсчёта;

 -[Ω×v] — инерционное ускорение, связанное с относительным движением.

Покажем, что уравнения (3) и (5) взаимно преобразуются. Обозначим -ω2·r + Ω2·r = -(ω2 - Ω2)·r = -ωs2·r, тогда

aτ = v·(v·as)/v2 = v·(v·(-ωs2·r - [Ω×v]))/v2 = v·(-ωs2·r·v - v·[Ω×v])/v2 = v·(-ωs2·r·v)/v2 = -ωs2·v·(r·v)/v2 = -ωs2·(r·v)·v/v2;

Ωs = [v×as]/v2 = [v×(-ωs2·r - [Ω×v])]/v2 = (-ωs2·[v×r] - v×[Ω×v])/v2 = (-ωs2·[v×r] - Ω·(v·v) + v·(v·Ω))/v2 = -ωs2·[v×r]/v2 - Ω = ωs2·[r×v]/v2 - Ω;

a = aτ + [Ωs×v] - [Ω×v] = -ωs2·(r·v)·v/v2 + [(ωs2·[r×v]/v2 - Ω)×v] - [Ω×v] = -ωs2·(r·v)·v/v2 + ωs2·[[r×v]×v]/v2 - 2·[Ω×v] = -ωs2·((r·v)·v + [v×[r×v]])/v2 - 2·[Ω×v] =

= -ωs2·((r·v)·v + r·(v2) - v·(v·r))/v2 - 2·[Ω×v] = -ωs2·r - 2·[Ω×v] = -ω2·r - 2·[Ω×v] + Ω2·r.

Уравнения (3) и (5) математически эквивалентны, но физически принципиально отличаются. ...

Обратите внимание, что когда тело не имеет идеальной связи с не ИСО, т. е. движется только на её фоне, то выражение -Ω2·r надо рассматривать, как дифференциальное уравнение кинематического движения по окружности в текущей точке координат. Поэтому в уравнении (3), член -Ω2·r, вычитается из результирующего ускорения в не ИСО, т. е. вычитается движение по окружности для наблюдателя r, который находится в этой системе, что физически не связано с наличием центробежной силы. Центробежная сила появляется только при наличии идеальной связи, и её в этом случае можно измерить. ...

 

[v×r] = [(i·vx + j·vy)×(i·rx + j·ry)] = i·j·vx·ry + j·i·vy·rx = k·(vx·ry - vy·rx).

vx·ry = (-a·ω·cos(ω·t)·cos(Ω·t) + a·Ω·sin(ω·t)·sin(Ω·t)  - b·ω·sin(ω·t)·sin(Ω·t) + b·Ω·cos(ω·t)·cos(Ω·t))·(a·sin(ω·t)·sin(Ω·t)  + b·cos(ω·t)·cos(Ω·t)) =

= -a2·ω·cos(ω·t)·cos(Ω·t)·sin(ω·t)·sin(Ω·t) - a·b·ω·cos(ω·t)2·cos(Ω·t)2 +

+ a2·Ω·sin(ω·t)2·sin(Ω·t)2 + a·b·Ω·sin(ω·t)·sin(Ω·t)·cos(ω·t)·cos(Ω·t) -

- a·b·ω·sin(ω·t)2·sin(Ω·t)2 - b2·ω·sin(ω·t)·sin(Ω·t)·cos(ω·t)·cos(Ω·t) +

+ a·b·Ω·cos(ω·t)·cos(Ω·t)·sin(ω·t)·sin(Ω·t) + b2·Ω·cos(ω·t)2·cos(Ω·t)2.

 

vy·rx = (a·ω·cos(ω·t)·sin(Ω·t)  + a·Ω·sin(ω·t)·cos(Ω·t) - b·ω·sin(ω·t)·cos(Ω·t) - b·Ω·cos(ω·t)·sin(Ω·t))·(-a·sin(ω·t)·cos(Ω·t) + b·cos(ω·t)·sin(Ω·t)) =

= -a2·ω·cos(ω·t)·sin(Ω·t)·sin(ω·t)·cos(Ω·t) + a·b·ω·cos(ω·t)2·sin(Ω·t)2 -

- a2·Ω·sin(ω·t)2·cos(Ω·t)2 + a·b·Ω·sin(ω·t)·cos(Ω·t)·cos(ω·t)·sin(Ω·t) +

+ a·b·ω·sin(ω·t)2·cos(Ω·t)2 - b2·ω·sin(ω·t)·cos(Ω·t)·cos(ω·t)·sin(Ω·t) +

+ a·b·Ω·cos(ω·t)·sin(Ω·t)·sin(ω·t)·cos(Ω·t) - b2·Ω·cos(ω·t)2·sin(Ω·t)2.

vx·ry - vy·rx =

= -a·b·ω·cos(ω·t)2·cos(Ω·t)2 + a2·Ω·sin(ω·t)2·sin(Ω·t)2 - a·b·ω·sin(ω·t)2·sin(Ω·t)2 + b2·Ω·cos(ω·t)2·cos(Ω·t)2 -

- a·b·ω·cos(ω·t)2·sin(Ω·t)2 + a2·Ω·sin(ω·t)2·cos(Ω·t)2 - a·b·ω·sin(ω·t)2·cos(Ω·t)2 + b2·Ω·cos(ω·t)2·sin(Ω·t)2 =

= -a·b·ω·cos(ω·t)2 + a2·Ω·sin(ω·t)2 - a·b·ω·sin(ω·t)2 + b2·Ω·cos(ω·t)2 =

= -a·b·ω + a2·Ω·sin(ω·t)2 + b2·Ω·cos(ω·t)2 = -a·b·ω + Ω·(a2·sin(ω·t)2 + b2·cos(ω·t)2) = -a·b·ω + Ω·R2.

Момент импульса маятника на единицу массы в относительном движении будет равен
pm = [r×v] = k·(a·b·ω - Ω·R2). Момент импульса зависит от текущего радиуса вращения.

ωs2 = ω2 - Ω2.

Закон сохранения энергии для маятника
ωs2·r2/2 + v2/2 = ωs2·a2/2 = const.

v2 = ωs2·a2 - ωs2·r2 = ωs2·(a2 - r2).

[v×as] = [v×[-ωs2·r - [Ω×v]]] = -ωs2·[v×r] - [v×[Ω×v]] = -ωs2·[v×r] - Ω·v2 = -k·ωs2·(-a·b·ω + Ω·R2) - Ω·v2 =

= -k·ωs2·(-a·b·ω + Ω·R2) - Ω·ωs2·(a2 - r2) = k·ωs2·a·b·ω - k·ωs2·Ω·R2 - Ω·ωs2·(a2 - r2) =

= k·ωs2·a·b·ω - k·ωs2·Ω·R2 - Ω·ωs2·a2 + Ω·ωs2·r2 = k·ωs2·a·b·ω - Ω·ωs2·a2 = k·ωs2·a·(b·ω - Ω·a), так как R2 = r2.

Ωs = [v×as]/v2 = [v0×as0]/v2 = P/v2 = k·a·(b·ω - Ω·a)/(a2 - r2). При условии b·ω = Ω·a; будет Ωs = 0.

 

rx·vx = (-a·sin(ω·t)·cos(Ω·t) + b·cos(ω·t)·sin(Ω·t))·(-a·ω·cos(ω·t)·cos(Ω·t) + a·Ω·sin(ω·t)·sin(Ω·t)  - b·ω·sin(ω·t)·sin(Ω·t) + b·Ω·cos(ω·t)·cos(Ω·t)) =

= a2·ω·sin(ω·t)·cos(ω·t)·cos(Ω·t)2 - a2·Ω·sin(ω·t)2·cos(Ω·t)·sin(Ω·t) + a·b·ω·sin(ω·t)2·cos(Ω·t)·sin(Ω·t) - a·b·Ω·sin(ω·t)·cos(ω·t)·cos(Ω·t)2 -

- a·b·ω·cos(ω·t)2·sin(Ω·t)·cos(Ω·t) + a·b·Ω·cos(ω·t)·sin(ω·t)·sin(Ω·t)2 - b2·ω·cos(ω·t)·sin(ω·t)·sin(Ω·t)2 + b2·Ω·cos(ω·t)2·sin(Ω·t)·cos(Ω·t).

 

ry·vy = (a·sin(ω·t)·sin(Ω·t)  + b·cos(ω·t)·cos(Ω·t))(a·ω·cos(ω·t)·sin(Ω·t)  + a·Ω·sin(ω·t)·cos(Ω·t) - b·ω·sin(ω·t)·cos(Ω·t) - b·Ω·cos(ω·t)·sin(Ω·t)) =

= a2·ω·sin(ω·t)·cos(ω·t)·sin(Ω·t)2 + a2·Ω·sin(ω·t)2·sin(Ω·t)·cos(Ω·t) - a·b·ω·sin(ω·t)2·sin(Ω·t)·cos(Ω·t) - a·b·Ω·sin(ω·t)·cos(ω·t)·sin(Ω·t)2 +

+ a·b·ω·cos(ω·t)2·cos(Ω·t)·sin(Ω·t) + a·b·Ω·cos(ω·t)·sin(ω·t)·cos(Ω·t)2 - b2·ω·cos(ω·t)·sin(ω·t)·cos(Ω·t)2 - b2·Ω·cos(ω·t)2·cos(Ω·t)·sin(Ω·t).

r·v = rx·vx + ry·vy = a2·ω·sin(ω·t)·cos(ω·t) - b2·ω·cos(ω·t)·sin(ω·t) = (a2 - b2)·ω·sin(ω·t)·cos(ω·t) = Rx·Vx + Ry·Vy = R·V.

Скалярное произведение радиус-вектора и скорости не зависит от вращения системы отсчёта.

Так как
Rx = -a·sin(ω·t); Vx = -a·ω·cos(ω·t);

Ry =  b·cos(ω·t); Vy = -b·ω·sin(ω·t).

Rx·Vx = a2·ω·sin(ω·t)·cos(ω·t);

Ry·Vy = -b2·ω·cos(ω·t)·sin(ω·t).

Этот результат предсказуем, так как длина векторов заданных в ИСО и угол между ними, не зависят от вращающейся системы отсчёта.

 

aτ = -ωs2·(r·v)·v/v2 = -ωs2·(a2 - b2)·ω·sin(ω·t)·cos(ω·t)·v/v2 = -(a2 - b2)·ω·sin(ω·t)·cos(ω·t)/(a2 - r2)·v.

Модуль тангенциального ускорения равен:
aτ = ωs2·(r·v)/v = ωs2·(R·V)/v = ωs·(R·V)/√(a2 - R2). При v = ωs·√(a2 - R2).
Модуль тангенциального ускорения, отвечающий за криволинейное поступательное движение, зависит от не ИСО только через множитель ωs = √(ω2 - Ω2).

Мощность, связанная с поступательным движением на единицу массы равна:
Np = aτ·v = ωs2·(R·V). В относительном движении часть мощности, связанной с Ω2, имеет виртуальный характер, но это не имеет принципиального значения при сохранении полной энергии.

Разность потенциалов при переходе между ИСО и не ИСО равна ΔЕ = Ω2·R2/2. ...

Угловая скорость вращения радиус-вектора равна:
pm = [r×v] = k·(a·b·ω - Ω·R2) = I·ωr = R2·ωr;

ωr = k·(a·b·ω/R2 - Ω). ...

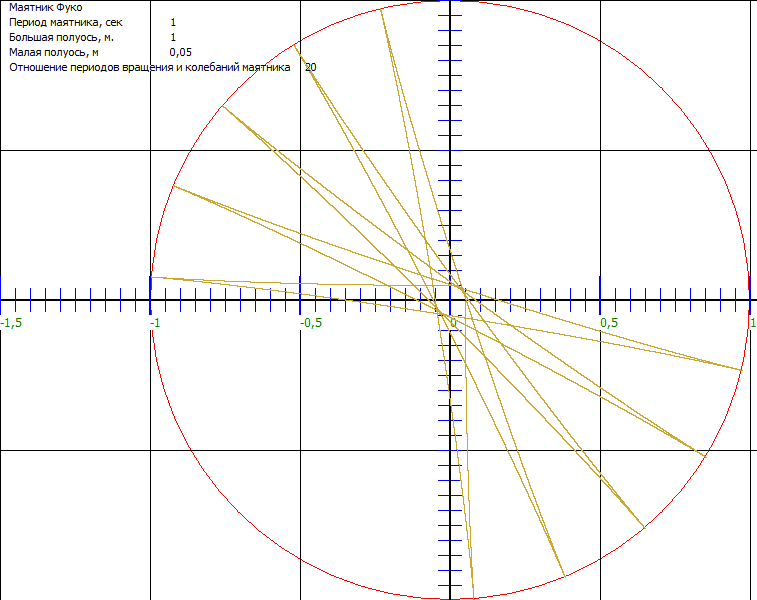
Маятник

Рассматривая уравнение a = -ω2·r - 2·[Ω×v] + Ω2·r (3) в более общем смысле, надо иметь ввиду, что оно справедливо только в двух случаях:

1. При наличии у тела идеальной связи с не ИСО, т. е. тело, перемещается на вращающейся платформе с наблюдателем находящимся в центре оси вращения, при угловой скорости Ω = const.

2. При относительном кинематическом вращении, когда наблюдатель находится в центре не ИСО с угловой скоростью Ω = const и наблюдает за движением тела в ИСО.

Однако, существует ещё третий вариант относительного движения на который как правило не обращают внимания.
Рассмотрим движение тела на вращающейся платформе с нулевой массой, вся масса сосредоточена в теле. В этом случае при движении тела его абсолютная скорость вращения меняется только по причине совершения работы центробежной силой и возможного действия момента сил со стороны оси вращения. Слагаемое, которое отвечает за движение через градиент скорости вращения, физически обнуляется (платформа не сопротивляется повороту, как в случае Ω = const). В этом варианте Ω уже не постоянная величина и можно записать:
a = -ω2·r - [Ω×v] + Ω2·r = -ω2·r - [Ω×v] - [Ω×[Ω×r]] = -ω2·r - [Ω×v] - [Ω×ve] = -ω2·r - [Ω×V] = -ω2·r - [ωr×V].
Тело находится в системе отсчёта с угловой скоростью вращения радиус-вектора ωr и движется с абсолютной скоростью V. Фактически вектор скорости v имеет только радиальную компоненту. Рассматривая это уравнение не надо забывать, что тело находится в условиях идеальной связи с невесомой платформой и в такой не ИСО уравнение справедливо только в силовом варианте записи (реально регистрируются силы, а не ускорения)
F = -m·ω2·r - m·[ωr×V] (6).
Это уравнение имеет физический смысл только при условии реального существования сил инерции, т. е. существование силы -m·[ωr×V], наблюдаемой в не ИСО в условиях идеальной связи, проявляется в ИСО через наличие относительного ускорения -[ωr×V], независимо от наличия сил, действующих по третьему и второму закону Ньютона. Это уравнение не нарушает закон сохранения энергии. Сила инерции W = -m·[ωr×V] в ИСО является гироскопической, т. е. не совершает работы и определяет свойство жёсткости пространства по отношению к вращательным движениям.
Например, тело массой m движется по окружности радиуса R = r. Упругая сила, действующая в не ИСО и формирующая круговую траекторию в ИСО равна
F = -m·ω2·r, тогда
F - m·[ωr×V] = 0, так как сила инерции скомпенсирована упругостью пружины; F = m·[ωr×V] (7). Центр масс, проходящий через ось вращения, покоится.

Ускорение наблюдаемое в ИСО равно
a = F/m = [ωr×V] = [ωr×[ωr×R]] = -ωr2·R = -V2/R. Получили ускорение Гюйгенса.

Если считать уравнение (3) только следствием кинематики относительного движения, то можно смело говорить о математической формальности силы инерции W, полученной переводом уравнения (3) в систему отсчёта с угловой скоростью радиус-вектора ωr. Однако уравнение (3) можно получить и из энергетических соображений, через уравнение Лагранжа. Энергия это уже не математический формализм, а реальная величина, с которой связаны все силовые процессы в природе. Поэтому просто отрицать реальность W без проверки опытом в этом случае уже не разумно. ...

Рассмотрим задачу на движение тела по гироскопической спирали. Например, тело движется к центру вращения с постоянной радиальной скоростью v. Задана начальная скорость вращения и радиус. На практике такое движение возможно только при полной диссипации энергии, связанной с работой центробежной силы (сопротивление среды, момент силы со стороны оси или что-то другое). Движение будет протекать по уравнению
a = [ωr×V] из (7).
Это уравнение при интегрировании даёт спиральную кривую, идущую к центру вращения с уменьшающимся шагом, так как при движении к центру, растёт частота вращения при скорости v = const. Угловая скорость радиус-вектора равна
ωr = (-Vx·sin(α) + Vy·cos(α))/R, где α — угол поворота радиус-вектора R. ...

Маятник на вращающейся платформе.

Оглавление
Форма входа
Старая форма входа
Поиск
Статистика
Онлайн всего: 1
Гостей: 1
Пользователей: 0
Copyright MyCorp © 2010-2025
Создать бесплатный сайт с uCoz