|
Движение центробежного вибратора в классическом варианте.
Задача решается на уровне почти школьной физики и математики.
Формально это задача на движение трёх тел, однако в силу симметрии устройства можно обойтись двумя векторными уравнениями.
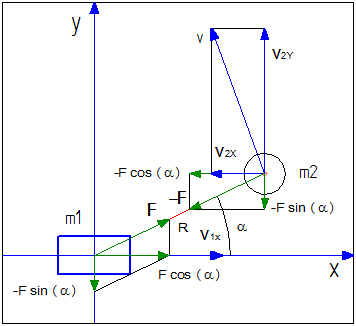
Составляем векторные уравнения для корпуса и грузов:
\(\displaystyle m_{1} \cdot \vec a_{1} = ~~~\vec F\);
\(\displaystyle m_{2} \cdot \vec a_{2} = -\vec F\),
где \(\displaystyle m_{1}-\) масса корпуса; \(\displaystyle m_{2}-\) суммарная масса грузов; \(\displaystyle \vec a_{1}-\) ускорение корпуса;
\(\displaystyle \vec a_{2}-\) ускорение грузов; \(\displaystyle \vec F-\) сила действующая через стержень, соединяющий корпус и грузы.
Проецируем на оси \(\displaystyle \mathbf{x}\) и \(\displaystyle \mathbf{y}\), ось \(\displaystyle \mathbf{x}\) направлена вдоль направления движения:
\(\displaystyle m_{1} \cdot a_{1x} = ~~~F \cdot cos(α)~~~~~~\) (1)
\(\displaystyle m_{2} \cdot a_{2x} =-F \cdot cos(α);~~~~\) (2)
\(\displaystyle m_{2} \cdot a_{2y} =-F \cdot sin(α);~~~~\) (3)
\(\displaystyle m_{1} \cdot a_{1y} = ~~~0.\) Так как движения корпуса по оси \( \displaystyle \mathbf{y}\) нет, где \(\displaystyle α -\) угол между осью \(\displaystyle \mathbf{x}\) и стержнем.
Суммируем (1) и (2).
\(\displaystyle m \cdot a_x = m_1 \cdot a_{1x} + m_2 \cdot a_{2x} = 0.~~\) (4) Центр масс покоится, где \(\displaystyle m = m_1 + m_2 \); \(\displaystyle a_x -\) ускорение центра масс.
Интегрируем (4) по времени.
\(\displaystyle m_1 \cdot v_{1x} + m_2 \cdot v_{2x} = C = 0.~~~~~~~~~~\) (5) Закон сохранения импульса, где \(\displaystyle v_{1x}-\) скорость корпуса;
\(\displaystyle v_{2x}-\) скорость грузов.
Кинематические соотношения по оси \(\displaystyle \mathbf{x}\), обусловленные устройством центробежного вибратора:
\(\displaystyle s_{2x}- s_{1x} = R \cdot cos(α) \), где \(\displaystyle s_{1x}-\) перемещение корпуса; \(\displaystyle s_{2x}-\) перемещение грузов, дифференцируем разность перемещений грузов и корпуса;
\(\displaystyle v_{2x} - v_{1x}= -R \cdot ω_z \cdot sin(α)\), где
\(\displaystyle ω_z -\) угловая скорость вращения грузов; \(\displaystyle R -\) длина стержня, соединяющего корпус и грузы.
\(\displaystyle v_{2x}+ ω_z R \cdot sin(α)= v_{1x}\).
Кинематические соотношения по оси \(\displaystyle \mathbf{y}\):
\(\displaystyle s_{2y}= R \cdot sin(α)\), дифференцируем перемещение грузов;
\(\displaystyle v_{2y}= ω_z R \cdot cos(α)\).
Подставляем \(\displaystyle v_{1x}\) в уравнение закона сохранения количества движения и находим скорость грузов по оси \(\displaystyle \mathbf{x}\):
\(\displaystyle m_1 (v_{2x} + ω_z R \cdot sin(α))+ m_2 \cdot v_{2x}= 0\);
\(\displaystyle m_1 \cdot v_{2x}+ m_1 \cdot ω_z R \cdot sin(α)+ m_2 \cdot v_{2x}= 0\);
\(\displaystyle m_1 \cdot ω_z R \cdot sin(α)+ (m_1 + m_2) v_{2x} = 0\);
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\) \(\displaystyle v_{2x}= -\left(\frac{m_1}{m} \right) ω_z R \cdot sin(α)\);
\(\displaystyle v_{1x} = v_{2x}+ ω_z R \cdot sin(α)\);
\(\displaystyle v_{1x} = ω_z R \cdot sin(α)- \left(\frac{m_1}{m} \right) ω_z R \cdot sin(α)\);
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\) \(\displaystyle v_{1x}= \left(\frac{m_2}{m} \right) ω_z R \cdot sin(α)\);
Используем закон сохранения энергии
\(\displaystyle \frac{m_{1} \cdot v_{1x}^2}{2}+ \frac{m_{2} \cdot v_{2x}^2}{2}+ \frac{m_{2} \cdot v_{2y}^2}{2} = E_{0}\),
где \(\displaystyle E_0 -\) суммарная энергия системы.
Подставляем скорости и подробно расписываем решение:
\( \displaystyle \frac{m_{1} \left(\frac{m_{2}}{m} ω_{z} R \cdot sin(α) \right)^2}{2} + \frac{m_{2} \left(\frac{m_{1}}{m} ω_{z} R \cdot sin(α) \right)^2}{2}+ \frac{m_{2} \left(ω_{z} R \cdot cos(α) \right)^2}{2}= E_{0}\);
\(\displaystyle m_{1} \left(\frac{m_{2}}{m} ω_{z} R \cdot sin(α) \right)^2 + m_{2} \left(\frac{m_{1}}{m} ω_{z} R \cdot sin(α) \right)^2 + m_{2} \left(ω_{z} R \cdot cos(α) \right)^2 = 2E_{0}\);
\(\displaystyle m_{1} \frac{m_{2}^2}{m^2} \left(ω_{z} R \cdot sin(α) \right)^2 + m_{2} \frac{m_{1}^2}{m^2} \left(ω_{z} R \cdot sin(α) \right)^2 + m_{2} \left(ω_{z} R \cdot cos(α) \right)^2 = 2E_{0}\);
\(\displaystyle \left(ω_{z} R \cdot sin(α) \right)^2 \left( m_{1} \frac{m_{2}^2}{m^2}+ m_{2} \frac{m_{1}^2}{m^2} \right) + m_{2} \left(ω_{z} R \cdot cos(α) \right)^2 = 2E_{0}\);
\(\displaystyle \frac{m_2 \cdot m_1}{m} \left(ω_{z} R \cdot sin(α) \right)^2 + m_{2} \left(ω_{z} R \cdot cos(α) \right)^2 = 2E_{0}\);
\(\displaystyle m_2 (ω_{z} R)^2 \left(\frac{m_1}{m} sin(α)^2 + cos(α)^2 \right) = 2E_{0}\);
\(\displaystyle m_2 (ω_{z} R)^2 \left(\frac{m_1}{m} sin(α)^2 + 1 - sin(α)^2 \right) = 2E_{0}\);
\(\displaystyle m_2 (ω_{z} R)^2 \left(1 - \frac{m_2}{m} sin(α)^2\right) = 2E_{0} = m_2 \cdot v_{2y0}^2\);
\(\displaystyle (ω_{z} R)^2 \left(1- \frac{m_2}{m} sin(α)^2\right) = v_{2y0}^2\);
\(\displaystyle ω_{z}^2 \left(1- \frac{m_2}{m} sin(α)^2\right)= \frac{v_{2y0}^2}{R^2}= ω_{z0}^2\), где \(\displaystyle ω_{z0}-\) угловая скорость грузов при \(\displaystyle α = 0\), когда корпус покоится, т. е. при максимальной энергии грузов.
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\) \(\displaystyle ω_z= \frac{ω_{z0}}{\sqrt{1- \frac{m_2}{m} sin(α)^2 }}= \frac{d α}{dt}\).
Найдем время
\(\displaystyle dt = \frac{1}{ω_{z0}} \sqrt{1- \frac{m_2}{m} sin(α)^2 }~ dα\).
Интегрируем это выражение
\(\displaystyle t= \frac{1}{ω_{z0}} \int\limits_{0}^{α} \sqrt{1- \frac{m_2}{m} sin(α)^2 }~ dα\).
Если ввести обозначение \(\displaystyle k= \sqrt{\frac{m_2}{m}} \); \(\displaystyle ~~T_0= \frac{2 \pi}{ω_{z0}}\), тогда
\(\displaystyle t= \frac{T_0}{2 \pi} \int\limits_{0}^{α} \sqrt{1- k^2 sin(α)^2 }~ dα\).
Время выражается через эллиптический интеграл второго рода, который аналитически не берётся и вычисляется по таблицам. Для вибратора с параметрами пружинного инерцоида
\(\displaystyle k= \sqrt{\frac{m_2}{m}}= \sqrt{\frac{0,26}{0,95}}= 0,52315 \); \(\displaystyle arcsin(0,52315)= 31,54°\).
На интервале интегрирования \(\displaystyle 0° - 90°\) по таблицам полных интегралов имеем:
\(\displaystyle 31° - 1,4608;\)
\(\displaystyle 32° - 1,4539.\)
Линейно интерполируем
\(\displaystyle \frac{1,4539- 1,4608}{32° - 31°} = -0,0069.\)
\(\displaystyle 1,4608- 0,0069 \cdot (31,54° - 31°) = 1,4608 - 0,0069 \cdot 0,54° = 1,457\). Это значение интеграла за четверть периода.
Значение интеграла на интервале \(\displaystyle 0° - 360°\) будет равно \(\displaystyle 4 \cdot 1,457 = 5,8282\).
\(\displaystyle T= \frac{5,8282}{2 \pi}= 0,9276\) сек при \(\displaystyle T_0 = 1\) cек.
Таким образом, период вращения грузов мало отличается от периода равномерного вращения по круговой орбите с той же энергией, всего на \(\displaystyle -7,2\) %.
Проинтегрируем уравнение закона сохранения импульса (5)
\(\displaystyle m_1 \cdot s_{1x}+ m_2 \cdot s_{2x}= C= 0\).
Добавляем кинематическое уравнение связи между перемещением грузов и корпуса
\(\displaystyle s_{2x}- s_{1x} = R \cdot cos(α)\).
\(\displaystyle s_{2x}= R \cdot cos(α)+ s_{1x}\).
\(\displaystyle m_1 \cdot s_{1x}+ m_2 (R \cdot cos(α)+ s_{1x})=0\).
\(\displaystyle m_1 \cdot s_{1x}+ m_2 \cdot R \cdot cos(α) + m_2 \cdot s_{1x}=0\).
\(\displaystyle m \cdot s_{1x}+ m_2 \cdot R \cdot cos(α)=0\).
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\) \(\displaystyle s_{1x}=- \frac{m_2}{m} R \cdot cos(α)\).
Найдем перемещение при повороте грузов в интервале \(\displaystyle 0° - 180°\).
\(\displaystyle Δs_{1x}= -\frac{m_2}{m} R \cdot (cos(180°)- cos(0°))= 2R \frac{m_2}{m}\).
В случае вибратора с параметрами пружинного инерцоида Толчина
\(\displaystyle Δs = 2R \frac{m_2}{m} = 2 \cdot 60 \frac{2 \cdot 0,13}{0,95} = 32,842\) мм. Это перемещение не зависит от внутренних силовых факторов.
Это очень важное свойство центробежного вибратора, на основе которого можно сразу увидеть несоответствие теории и опыта.
Из опыта известно, что инерцоид с тактовым периодом \(1\) сек проходит за такт примерно \(60~мм\).
Рассмотрим первый мысленный эксперимент.
Пусть центр масс вибратора движется с постоянной скоростью \(60\) мм/с.
Тактовый период \(T=1\) сек. Период каждого полутакта вибратора равен \(\displaystyle T_1=T_2 = \frac{T}{2} = 0,5\) сек, тогда:
За время отката назад корпус вибратора проедет расстояние
\(60~мм/2- 32,842= -2,842~мм\);
За время хода вперёд корпус вибратора проедет расстояние
\(60~мм/2+ 32,842 = 62,842~мм\);
В сумме \(60\) мм.
Рассмотрим второй мысленный эксперимент.
Пусть центр масс вибратора движется со скоростью \(60~мм/с\). Тактовый период \(T = 1~сек\). Период каждого полутакта разный. Возьмём крайний случай, когда при ходе корпуса вперёд период очень маленький и можно считать, что за это время центр масс вибратора практически останется на месте, т. е., полагаем в пределе \(T_1~→ 0\). Это означает, что ход назад составляет по времени практически период, т. е. \(T = T_2~ → 1~ сек\) \( (T_1 + T_2 = T)\), тогда:
За время отката назад корпус вибратора проедет расстояние
\(60~мм - 32,8421 = 27,1579~мм\);
За время хода вперёд корпус вибратора проедет расстояние
\(0~мм + 32,842 = 32,842~мм\).
В сумме \(60~мм\).
Для промежуточных вариантов соотношения времени хода вперёд и отката назад можно записать:
Откат корпуса назад будет в диапазоне \(-2,8421~мм- 27,1579~мм\);
Ход корпуса вперёд будет в диапазоне \(62,8421~мм- 32,8421~мм\).
Обратите внимание, что при нулевой скорости центра масс:
Откат \(-32,842~мм\);
Ход вперёд \(+32,842~мм\).
В сумме \(0~мм\).
А теперь, задумайтесь над тем, как должно влиять трение на движение вибратора, чтобы обеспечить движение корпуса в соответствии с экспериментом при средней скорости \(60~мм/с\):
Откат \(-30~мм\);
Ход вперёд \(+90~мм\).
В сумме \(+60~мм\).
Значение отката назад равное \(-30~мм\) можно получить только в том случае, если центр масс за время отката, в среднем практически покоится, его среднее перемещение вперёд не должно превышать \(2,842~мм\). Тогда возникает вопрос, как после такого отката, при ходе вперед получается \(90~мм\), когда должно быть около \(32,84~мм\), так как в начале хода вперёд скорость центра масс практически нулевая. Если трение при откате назад увеличивать, то величина отката будет только уменьшаться. Получить откат в \(-30~мм\) можно только при трении, которое практически не влияет на колебательный процесс вибратора. А ведь именно трение при движении назад в академическом варианте объяснения движения инерцоида является базовым, при этом предполагается, что трение вперёд получается меньше из-за большей скорости движения корпуса (Соснин). В классическом варианте импульс силы при ходе корпуса вперёд меньше не только по причине меньшего времени взаимодействия, но и по причине снижения трения. При использовании подшипников качения трение практически не зависит от скорости (жидкая смазка) в реальном диапазоне скоростей инерцоида, о чём лукаво молчат, акцентируя всё внимание на график трения сухих поверхностей, тем самым совершенно игнорируя эксперименты Толчина.
Нелепость академической позиции, особенно становится ясной, при численном анализе движения вибратора, построенного по классической теории.
Программа виброхода, Страница_4.
Найдём скорость корпуса через угол поворота:
\(\displaystyle v_{1x}=γ \cdot ω_z R \cdot sin(α);~~ γ = \frac{m_2}{m};\)
\(\displaystyle ω_z = \frac{ω_{z0}}{\sqrt{1- γ \cdot sin(α)^2}}\);
\(\displaystyle v_{1x}= \frac{γ \cdot ω_{z0} R \cdot sin(α)}{\sqrt{1 - γ \cdot sin(α)^2 }}\).
Максимальная скорость корпуса будет при \(α = 90°\).
\(\displaystyle v_{max~1x}=\frac{γ \cdot ω_{z0} R}{\sqrt{1-γ}}=\frac{γ \cdot v_{α=0}}{\sqrt{1-γ}}\), где \(v_{α=0}-\) скорость при \(α = 0\).
Например, при \(γ=0,2737\); \(\displaystyle \frac{γ}{\sqrt{1-γ}} = 0,3768\); \(ν = 1~Гц\), будет \(v_{max~1x}=14,2~см/с\).
Если центр масс виброхода движется с большей скоростью, трение уже не может его ускорять в направлении движения.
Найдём ускорение корпуса дифференцируя \(\displaystyle v_{1x} = γ \cdot ω_z R \cdot sin(α)\);
\(\displaystyle a_{1x}= γ \cdot ω_z^2 R \cdot cos(α)+ γ \frac{dω_z}{dt} R \cdot sin(α)\);
Найдём угловое ускорение из \(\displaystyle ω_z = \frac{ω_{z0}}{\sqrt{1- γ \cdot sin(α)^2}}\).
\(\displaystyle \frac{dω_z}{dt} = (-1/2) \cdot ω_{z0} (1- γ \cdot sin(α)^2)^{-3/2} (-2γ \cdot sin(α) \cdot cos(α) \cdot ω_z)=\)
\(\displaystyle = ω_{z0} (1- γ \cdot sin(α)^2)^{-3/2} \cdot γ \cdot sin(α) \cdot cos(α) \cdot ω_z =\)
\(\displaystyle = ω_{z0} (1-γ \cdot sin(α)^2)^{-3/2} \cdot γ \cdot sin(α) \cdot cos(α) \cdot ω_{z0}(1- γ \cdot sin(α)^2)^{-1/2}.\)
\(\displaystyle \frac{dω_z}{dt}=\frac{γ \cdot ω_{z0}^2 \cdot sin(α) \cdot cos(α)}{(1-γ \cdot sin(α)^2)^{2}}.\)
\(\displaystyle a_{x1}=\frac{γ \cdot ω_{z0}^2 R \cdot cos(α)}{1-γ \cdot sin(α)^2}+ \frac{γ^2 \cdot ω_{z0}^2 R \cdot sin(α)^2 \cdot cos(α)}{(1-γ \cdot sin(α)^2)^2}\);
\(\displaystyle a_{x1}=\frac{γ \cdot ω_{z0}^2 R \cdot cos(α)}{1-γ \cdot sin(α)^2} \left(1+\frac{γ \cdot sin(α)^2}{1-γ \cdot sin(α)^2}\right)\);
\(\displaystyle a_{x1}=\frac{γ \cdot ω_{z0}^2 R \cdot cos(α)}{(1-γ \cdot sin(α)^2)^2}\);
\(~~~~~~~~\) \(\displaystyle a_{x1}=\frac{γ \cdot ω_{z}^2 R \cdot cos(α)}{1-γ \cdot sin(α)^2}\).
Найдем силу, действующую на корпус при: \(α=0°\); \(α=45°\); \(α=60°\); \(α=80°\), и частоте вращения в медленном полутакте
\(ν_0=0,5~Гц\) \((T_0=2~сек)\), т. е. при \(T=1~сек\); \(T_2 = 0,93~сек\); \(T_1=0,07~сек\).
\(F_{1~α=0°}=11,40~грамм\).
\(F_{1~α=45°}=10,82~грамм\).
\(F_{1~α=60°}=9,03~грамм\).
\(F_{1~α=80°}=3,67~грамм\).
Эти значения силы практически минимальны при \(T = 1~сек\), так как время \(T_1\) составляет всего 7% от периода \(T\). В реальном опыте сила, действующая на корпус несколько больше.
В своих опытах Толчин изучал работу инерцоида и при частоте порядка \(ν=4~Гц\). Скорость движения в этом случае возрастала в 4 раза и центростремительные силы в 16 раз. Относительная роль сил трения уменьшается соответственно тоже в 16 раз, но это не привело к изменению характера движения механизма. Заметим, что, если учитывать предположения Соснина, то влияние трения должно уменьшиться более чем в 16 раз, так как инерцоид в этом случае работает в зоне спада величины трения в зависимости от скорости.
Введем в уравнение ускорения корпуса составляющую, связанную с наличием трения.
Формально можно записать так
\(\displaystyle a_{1x}= γ \cdot ω_z^2 R \cdot cos(α)+ γ \frac{dω_z}{dt} R \cdot sin(α)+ \frac{F_{тр}}{m_1}\), однако это будет не полный учёт трения.
Проблема в том, что влияние силы трения через стержень передаётся на грузы. Сила растяжения в стержне в этом случае равна
\(\displaystyle F= m_1 γ \cdot ω_z^2 R- \frac{m_2}{m} \frac{F_{тр}}{cos(α)}\), тогда \(\displaystyle \left(...+ \frac{F_{тр}}{m_1}- \frac{m_2}{m} \frac{F_{тр}}{m_1}= ...+\frac{F_{тр}}{m} \right)\)
\(\displaystyle a_{1x}= γ \cdot ω_z^2 R \cdot cos(α)+ γ \frac{dω_z}{dt} R \cdot sin(α)+ \frac{F_{тр}}{m}\). (9)
Найдем перемещение корпуса при \(F_{тр}=0\), через двойной интеграл от проекции центробежного ускорения:
\(\displaystyle s_{1x}=γ \int \int ω_z^2 R \cdot cos(α)~dt~dt\), сделаем замену переменной интегрирования;
\(\displaystyle s_{1x}=γ R \int \int cos(α)~ω_z dt~ω_z dt=γ R \int \int cos(α)~dα~dα= γ R \int sin(α)~dα= -γ R \cdot cos(α)\).
Обратите внимание, что этот интеграл не зависит от угловой скорости. Независимость от угловой скорости фактически означает независимость амплитуды перемещения от внутренних моментов, действующих на рычаги.
При наличии трения, внутренние моменты оказывают влияние на кинематику корпуса относительно опоры, но это влияние не значительно и численный анализ показывает, что сочетание трения и внутренних силовых моментов не может быть причиной фактического движения инерцоида.
В различных источниках можно встретить формулу \(\displaystyle a_{1x}= \frac{m_2}{m} ω_z^2 R \cdot cos(α)\) или
\(\displaystyle a_{1y}= \frac{m_2}{m} ω_z^2 R \cdot sin(α)\), через которую авторы пытаются обосновать возможность поступательного движения центробежных движителей, совершенно игнорируя свойства этой функции, её происхождение. Эта функция на замкнутом пути всегда даёт нулевое перемещение корпуса. В будущем при решении задачи для инерцоида мы увидим, что решение для свободного вибратора тоже входит в это решение, но и там оно не даёт поступательного движения. Обратите на это особое внимание. Причина поступательного движения лежит глубже.
Рассмотрим эту задачу в более общем виде с учётом трения со стороны опоры и силовых моментов, действующих на грузы.
Введем обозначения: \(\displaystyle \vec F_m= \frac{\left[\vec M × \vec R \right]}{R^2}= \left[\frac{\vec M}{\vec R} \right]-\) сила, действующая на груз из-за наличия момента сил.
\(m_1 \cdot \vec a_1=~~~ \vec F+ \vec F_{тр}- [\vec M / \vec R]\);
\(m_2 \cdot \vec a_2=- \vec F+ ~~~~~~~~~~~ [\vec M / \vec R]\).
Проецируем на координатные оси и решаем задачу только в плоскости:
\(\displaystyle [\vec M / \vec R]= \frac{\left[\vec M × \vec R \right]}{R^2}= \frac{- \vec i \cdot M_z R_y + \vec j \cdot M_z R_x}{R^2}= \frac{- \vec i \cdot M_z \cdot sin(α)}{R}+ \frac{\vec j \cdot M_z \cdot cos(α)}{R}\), где α – угол между осью «x» и стержнем.
\(F_{1x}= ~~~F \cdot cos(α)\);
\(F_{2x}= -F \cdot cos(α) \), где \(F-\) модуль силы растяжения стержня;
\(F_{2y}= -F \cdot sin(α) \).
\(\displaystyle m_1 \cdot a_{1x}= ~~~F \cdot cos(α)+ F_{тр}+ \frac{M_z \cdot sin(α)}{R}\);
\(\displaystyle m_2 \cdot a_{2x}= -F \cdot cos(α) ~~~~~~~~~~~-\frac{M_z \cdot sin(α)}{R}\);
\(\displaystyle m_2 \cdot a_{2y}= -F \cdot sin(α) ~~~~~~~~~~~+\frac{M_z \cdot cos(α)}{R}\);
\(\displaystyle m_1 \cdot a_{1y}= 0\), так как поперечного движения корпуса нет.
Эту систему уравнений будем использовать в численной модели виброхода. Найдём ускорение центра масс по оси x.
\(m \cdot a_x= m_1 \cdot a_{1x}+ m_2 \cdot a_{2x}= F_{тр}\).
Ускорение центра масс зависит только от трения об опору. Момент сил влияет на движение центра масс только косвенно через скорость движения корпуса.
...
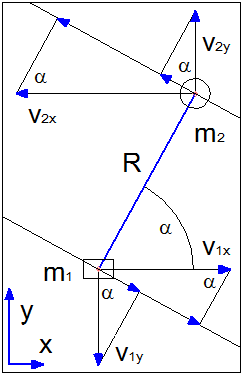
Угловая скорость вращения двух тел связанных жестким стержнем равна:
\(\displaystyle ω_z = \frac{(v_{1x}-v_{2x})sin(α)+(v_{2y}-v_{1y})cos(α)}{R}\).
Докажем эту формулу.
\(s_{2x}-s_{1x}=R \cdot cos(α)\); \(~~~~~~~~\) \(s_{2y}-s_{1y}=R \cdot sin(α)\);
\(\displaystyle v_{2x}-v_{1x}=-ω_z R \cdot sin(α)+ \frac{dR}{dt} cos(α)\); \(~~~~~~~\) \(\displaystyle v_{2y}-v_{1y}=ω_z R \cdot cos(α)+ \frac{dR}{dt} sin(α)\);
\(\displaystyle ω_z = ω_z R \cdot \frac{sin(α) \cdot sin(α)}{R}+ ω_z R \cdot \frac{cos(α) \cdot cos(α)}{R}\).
Покажем, что справедлива также формула для модуля угловой скорости
\(\displaystyle ω_z= \frac{\sqrt{(v_{1x}-v_{2x})^2+(v_{2y}-v_{1y})^2}}{R}\);
\(\displaystyle ω_z= \frac{\sqrt{(ω_z R \cdot sin(α))^2+(ω_z R \cdot cos(α))^2}}{R}\), только при условии \(\displaystyle \frac{dR}{dt}=0\).
Покажем, что угловое ускорение при вращении двух тел связанных жестким стержнем равно:
\(\displaystyle \frac{dω_z}{dt}= \frac{(a_{1x}-a_{2x})sin(α)+(a_{2y}-a_{1y})cos(α)}{R}\).
Так как \(\displaystyle a_{2x}-a_{1x}=-ω_z^2 R \cdot cos(α)- \frac{dω_z}{dt} R \cdot sin(α)\); \(~~~~~~~\) \(\displaystyle a_{2y}-a_{1y}= -ω_z^2 R \cdot sin(α)+ \frac{dω_z}{dt} R \cdot cos(α)\);
\(\displaystyle \frac{dω_z}{dt}= \frac{(ω_z^2 R \cdot cos(α)+ \frac{dω_z}{dt} R \cdot sin(α)) \cdot sin(α)}{R}+ \frac{(-ω_z^2 R \cdot sin(α)+ \frac{dω_z}{dt} R \cdot cos(α)) cos(α)}{R}=\)
\(\displaystyle = \frac{\frac{dω_z}{dt} R \cdot sin(α) \cdot sin(α)}{R}+ \frac{\frac{dω_z}{dt} R \cdot cos(α) \cdot cos(α)}{R}\).
Для центробежного вибратора эти формулы можно записать без координаты \(s_{1y}\)
\(\displaystyle ω_z= \frac{(v_{1x}-v_{2x})sin(α)}{R}+ \frac{v_{2y} \cdot cos(α)}{R}\);
\(\displaystyle ω_z= \frac{\sqrt{(v_{1x}-v_{2x})^2+ v_{2y}^2}}{R}\);
\(\displaystyle \frac{dω_{z}}{dt}=\frac{(a_{1x}-a_{2x}) \cdot sin(α)}{R}+ \frac{a_{2y} \cdot cos(α)}{R}\). (6)
Обратите внимание, что для вычисления этих функций надо знать кинематические параметры грузов и корпуса одновременно. Однако, существует ещё одно дополнительное условие на угловое ускорение. Например, в статье Е. Л. Тарунина под названием, «Влияние трения на движение инерцоида» за 1996 г., в процессе вычисления у Евгения Леонидовича получается следующее уравнение для углового ускорения рычага вибратора, полученное из уравнения Лагранжа.
\(\displaystyle \frac{d\omega_z}{dt}=a_{1x}\cdot\frac{sin(\alpha)}{R}+ \frac{M_z}{I_2}\), где \(I_2-\) момент инерции грузов \(I_2=m_2 \cdot R^2\). Для свободного вибратора \(M_z=0\), тогда
\(\displaystyle \frac{dω_{z}}{dt}= \frac{a_{1x} \cdot sin(α)}{R}\). (7)
Перепишем (6) в следующем варианте
\(\displaystyle \frac{dω_{z}}{dt}= \frac{a_{1x} \cdot sin(α)}{R}+ \frac{a_{2y} \cdot cos(α)- a_{2x} \cdot sin(α)}{R}.\) (8)
Сравнивая (7) и (8) получим \(a_{2y} cos(α)- a_{2x} sin(α)=0\). Проверка численным способом, показывает, что это условие справедливо, \(a_{2y}=a_{2x} tg(α)\).
Рассмотрим решения, которые удовлетворяют этому дифференциальному уравнению – условию, например
\(a_{2yr}= -ω_{z}^2 R \cdot sin(α)\); \(~~~~~~~~\) \(a_{2xr}= -ω_{z}^2 R \cdot cos(α)\), так как \(V_{τ}= ω_{z} R\), то
\(a_{2yr}= -ω_{z} V_τ \cdot sin(α)\); \(~~~~~~~\) \(a_{2xr}= -ω_{z} V_τ \cdot cos(α)\);
\(a_{2yr}= ω_{z} V_{τx}\); \(~~~~~~~\) \(a_{2xr}= -ω_{z} V_{τy}\);
\(\vec a_{2r}= [\vec ω_{z}× \vec V_τ]\);
В этом случае ускорение грузов имеет гироскопический характер относительно окружной скорости.
Из (7) следует
\(\displaystyle a_{2τ}= R \frac{dω_{z}}{dt}= a_{1x} \cdot sin(α)-\) окружное ускорение грузов зависит только от ускорения корпуса.
В более общем векторном виде это можно записать так
\(\displaystyle \vec a_2=\vec τ \cdot R \frac{dω_{z}}{dt}+[\vec ω_z × \vec V_τ]= \vec τ \cdot a_{1x} \cdot sin(α)+[\vec ω_z × \vec V_τ]\).
Для любого ускорения \(\vec a_2 \) направленного вдоль стержня, выражение \(\displaystyle \frac{a_{2y} \cdot cos(α)-a_{2x} \cdot sin(α)}{R}= \frac{a_2 \cdot sin(α) \cdot cos(α)-a_2 \cdot cos(α) \cdot sin(α)}{R}=0\).
Если в уравнение (8) подставить ускорение грузов под действием момента сил, то получим
\(\displaystyle \frac{dω_{z}}{dt}= \frac{a_{1x} \cdot sin(α)}{R}+ \frac{a_{2y} \cdot cos(α)-a_{2x} \cdot sin(α)}{R}=\)
\(\displaystyle = \frac{a_{1x} \cdot sin(α)}{R}+ \frac{\left(\frac{M_z \cdot cos(α)}{R \cdot m_2} cos(α)+ \frac{M_z \cdot sin(α)}{R \cdot m_2} sin(α) \right)}{R}=\)
\(\displaystyle = \frac{a_{1x} \cdot sin(α)}{R} + \frac{M_{z}}{m_{2} R^2}\).
$ \displaystyle \frac{dω_{z}}{dt}= \frac{a_{1x} \cdot sin(α)}{R}+ \frac{M_{z}}{I_2} $.
Используем уравнение (9)
\(\displaystyle a_{1x}=γ \cdot ω_{z}^2 \cdot R \cdot cos(α)+ γ \cdot \frac{dω_{z}}{dt}\cdot R \cdot sin(α)+ \frac{F_{тр}}{m}\);
$ \displaystyle a_{1x}=γ \cdot ω_{z}^2 \cdot R \cdot cos(α)+ γ \cdot \left(\frac{a_{1x} \cdot sin(α)}{R}+ \frac{M_{z}}{I_2} \right) \cdot R \cdot sin(α) + \frac{F_{тр}}{m} $;
$ \displaystyle a_{1x}=γ \cdot ω_{z}^2 \cdot R \cdot cos(α)+ γ \cdot a_{1x} \cdot sin(α)^2 + γ \cdot \frac{M_{z} \cdot R \cdot sin(α)}{I_2} + \frac{F_{тр}}{m} $;
$ \displaystyle a_{1x}-γ \cdot a_{1x} \cdot sin(α)^2= γ \cdot ω_{z}^2 \cdot R \cdot cos(α)+ \frac{M_{z} \cdot sin(α)}{m_2 R}+ \frac{F_{тр}}{m} $;
$ \displaystyle a_{1x}= \frac{γ \cdot ω_{z}^2 \cdot R \cdot cos(α)+ \frac{M_{z} \cdot sin(α)}{m_2 R}+ \frac{F_{тр}}{m} }{1- γ \cdot sin(α)^2}. $
Дифференциальные уравнения движения вибратора через уравнения Лагранжа.
Найдём полную кинетическую энергию системы корпус+грузы.
$ \displaystyle L= \frac{ m_{1} \cdot v_{1x}^2}{2}+ \frac{ m_{2} \cdot (v_{2x}^2 + v_{2y}^2)}{2}. $
Так как $ \displaystyle v_{2x} = v_{1x} - ω_{z} \cdot R\cdot sin(α) $ и $ \displaystyle v_{2y} = ω_{z} \cdot R\cdot cos(α) $, то
$ \displaystyle L = \frac{m_{1} \cdot v_{1x}^2}{2} + \frac{m_{2} \cdot ((v_{1x}- ω _{z} \cdot R \cdot sin(α))^2+ (ω _{z} \cdot R \cdot cos(α))^2)}{2} = $
$ \displaystyle = \frac{m_{1} \cdot v_{1x}^2}{2} + \frac{m_{2} \cdot (v_{1x}^2 + ω _{z}^2 \cdot R^2 \cdot sin(α)^2 - 2 \cdot v_{1x} \cdot ω _{z} \cdot R \cdot sin(α)+ ω _{z}^2 \cdot R^2 \cdot cos(α)^2)}{2}; $
$ \displaystyle L = \frac{m \cdot v_{1x}^2}{2} + \frac{m_{2} \cdot (ω _{z}^2 \cdot R^2 - 2 \cdot v_{1x} \cdot ω _{z} \cdot R \cdot sin(α))}{2}; $
Запишем уравнение Лагранжа для координат корпуса
$ \displaystyle \frac {d} {dt} \left(\frac{\partial L}{\partial v_{1x}} \right) - \frac{\partial L}{\partial x_{1}} = F_{тр};$
Находим производные
$ \displaystyle \frac{\partial L}{\partial v_{1x}} = m \cdot v_{1x} - m_{2} \cdot ω _{z} \cdot R \cdot sin(α); $
$ \displaystyle \frac {d} {dt} \left(\frac{\partial L}{\partial v_{1x}} \right) = m \cdot a_{1x} - m_{2} \cdot \frac{dω _{z}} {dt} \cdot R \cdot sin(α) - m_{2} \cdot ω _{z}^2 \cdot R \cdot cos(α); $
$ \displaystyle \frac{\partial L}{\partial x_{1}} = 0 $, тогда
$ \displaystyle m \cdot a_{1x}- m_{2} \cdot \frac{dω_{z}} {dt} \cdot R \cdot sin(α) - m_{2} \cdot ω _{z}^2 \cdot R \cdot cos(α) = F_{тр}; $
\(\displaystyle m \cdot a_{1x}= m_{2} \cdot ω_{z}^2 \cdot R \cdot cos(α) + m_{2} \cdot \frac{dω _{z}} {dt} \cdot R \cdot sin(α) + F_{тр};\)
\(\displaystyle a_{1x}=\gamma \cdot \omega_{z}^2 \cdot R\cdot cos(α) + γ \cdot \frac{dω_{z}} {dt} \cdot R \cdot sin(α)+\frac{F_{тр}} {m}.\) (10)
Это уравнение интегрируется на интервале времени при \(F_{тр} = const\)
\(\displaystyle v_{1x} = \gamma \cdot \omega_z \cdot R \cdot sin(α) + \frac{F_{тр}}{m}\cdot t + v_{1x0};\)
\(\displaystyle s_{1x} = -\gamma \cdot R \cdot cos(α) + \frac{1}{2}\frac{F_{тр}}{m}\cdot t^2 + v_{1x0}\cdot t + s_{1x0}.\)
Запишем уравнение Лагранжа для угла поворота грузов
\(\displaystyle \frac{d}{dt}\left(\frac{\partial L}{\partial\omega_z}\right) - \frac{\partial L}{\partial\alpha} = M_z;\)
Находим производные
\(\displaystyle \frac{\partial L}{\partial\omega_z} = m_2\cdot\omega_z\cdot R^2 - m_2\cdot v_{1x}\cdot R\cdot sin(\alpha);\)
\( \displaystyle \frac{d}{dt}\left(\frac{\partial L}{\partial\omega_z}\right) = m_2\cdot\frac{d\omega_z}{dt}\cdot R^2 - m_2\cdot a_{1x}\cdot R\cdot sin(\alpha)- m_2\cdot v_{1x}\cdot \omega_z\cdot R\cdot cos(\alpha);\)
\(\displaystyle \frac{\partial L}{\partial\alpha}= - m_2\cdot v_{1x}\cdot \omega_z\cdot R\cdot cos(\alpha);\)
\(\displaystyle m_2\cdot\frac{d\omega_z}{dt}\cdot R^2 - m_2\cdot a_{1x}\cdot R\cdot sin(\alpha) = M_z;\)
\(\displaystyle \frac{d\omega_z}{dt}- a_{1x}\cdot\frac{sin(\alpha)}{R} = \frac{M_z}{I_2};\)
\(\displaystyle \frac{d\omega_z}{dt} = a_{1x}\cdot\frac{sin(\alpha)}{R} + \frac{M_z}{I_2}.\) (11)
Объединим дифференциальные уравнения (10) и (11).
\(\displaystyle \frac{d\omega_z}{dt} (1-\gamma \cdot sin(\alpha)^2 )=\gamma \cdot \omega_z^2 \cdot cos(\alpha) sin(\alpha) + \frac{F_{тр}}{m R} \cdot sin(\alpha) + \frac{M_z}{I_2}\). (12)
Решим систему из уравнений (10) и (12) в среде Mathcad'a при разных параметрах, определяющих движение вибратора.
Составим блок решения.
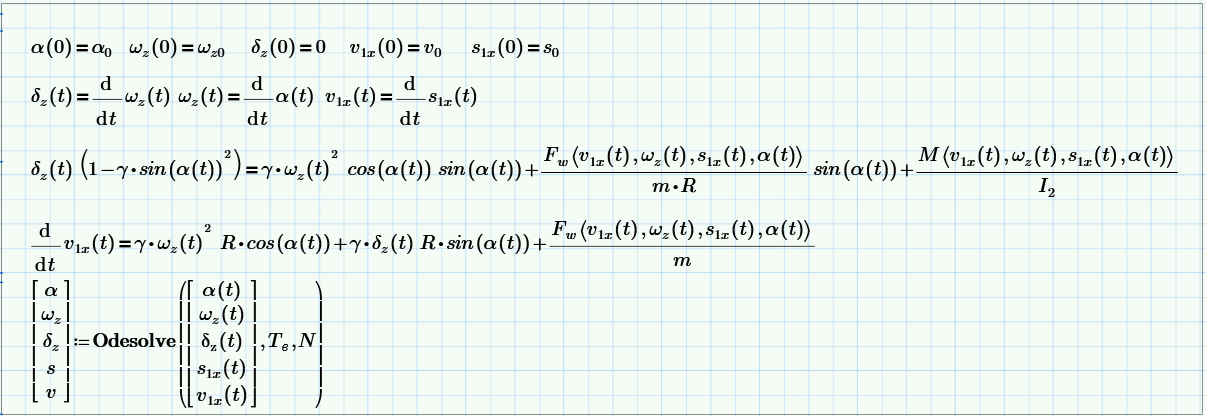
Перечислим общие параметры и функции, необходимые для вычислений.
\(g=9,80665~м/c^2-\) стандартное ускорение.
\(I_2=m_2 \cdot R^2=9,36 \cdot 10^{-4}~кг \cdot м^2-\) суммарный момент инерции грузов.
\(\displaystyle \gamma=\frac{m_2}{m}=0,2737-\) параметр центробежного вибратора.
\(ω_{z0}=2 \pi ν,~с^{-1}-\) начальная угловая скорость грузов.
\(q=g/1000-\) перевод грамм в Ньютоны для функции трения.
\(к=-4000-\) коэффициент для функции трения. Формирует фронт прямоугольного импульса.
\(F_w(v,\omega,s,\alpha)=q \cdot F_t \cdot tanh(к \cdot v)-\) функция трения.
\(m_1=0,69~кг-\) масса корпуса.
\(m_2=0,26~кг-\) суммарная масса грузов.
\(m=m_1+m_2=0,95~кг-\) полная масса вибратора.
\(R=0,06~м-\) радиус движения грузов.
\(N=T_в \cdot 5000=20000-\) количество расчётных точек.
\(\alpha_0=0-\) начальное угловое положение грузов.
\(v_0=0~м/с-\) начальная скорость корпуса.
\(s_0=0~м-\) исходная координата корпуса.
Параметры для текущей серии графиков.
\(T_в=4~сек-\) период расчёта движения.
\(ν=1~Гц-\) мгновенная частота вращения грузов при \(\alpha=0\).
\(F_t=0~грамм-\) модуль трения колёс.
\(M=0-\) момент действующий на грузы.
График колебаний корпуса вибратора.
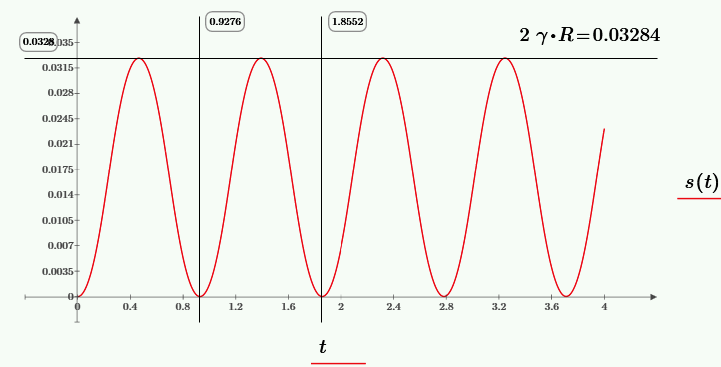
График угловой скорости грузов.
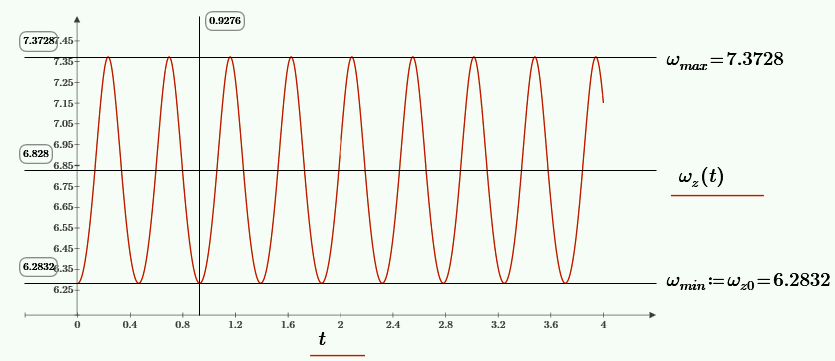
Колебания угловой скорости появляются в результате обмена энергией между грузами и корпусом вибратора.
Колебания угла перемещения грузов в сравнении с равномерным вращением.
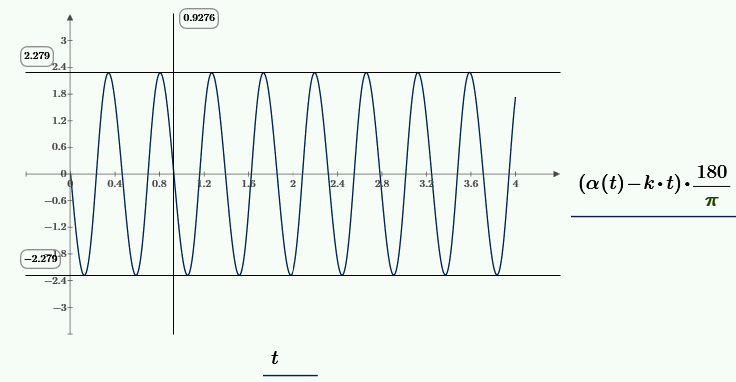
Размах колебаний угла равен \(4,56°\).
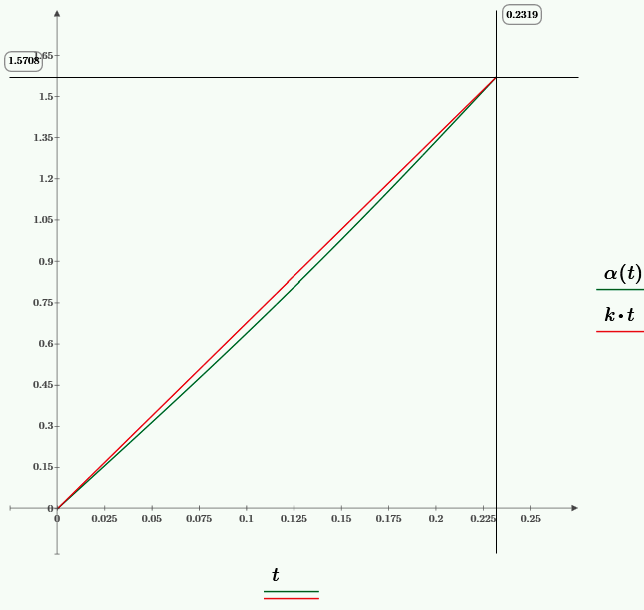
...

Оглавление
Продолжение
|

