Для понимания состояния современной механики относительного движения в неинерциальных системах отсчёта, процитируем книгу "Инерция" Н. В. Гулиа 1982 г. Несмотря на давность этого источника, в современных официальных представлениях мало что изменилось. Текст Гулиа правильно отражает сложившуюся философию механических взглядов.

Механика относительного движения и эйлеровы силы инерции.

«Во многих разделах механики и её приложений к техническим наукам движение материальных точек и тел изучается по отношению к подвижным телам большой массы. Движение последних считается практически не зависящим от изучаемого движения сравнительно небольших масс и обычно заранее задаётся. Например, при изучении колебаний маятников на корабле, движение атмосферы и рек по отношению к Земле, поведение гироскопов на самолёте можно смело считать, что движение корабля, Земли и самолёта остаётся неизменным. При рассмотрении этих достаточно сложных явлений, как и в предыдущих примерах, необходимо чёткое разграничение реальных физических сил и сил инерции.
     Как уже говорилось, реальными мы считаем силы, вызывающие ускорение материальных точек и тел относительно "абсолютной" системы координат, или (что одно и то же) инерциальной системы отсчёта. Эти силы выражают меру механического взаимодействия тел и могут быть различны по своей природе: ... В конечном счёте, реальная физическая сила измеряется производимым ею ускорением единицы массы в инерциальной ("абсолютной") системе отсчёта.
     При изучении механики относительного движения важно отличать даламберовы силы инерции и силы инерции, вводимые при рассмотрении движения материальных точек и тел по отношению к подвижным (неинерциальным) системам отсчёта. Эти последние, по предложению академика А. Ю. Ишлинского, будем называть эйлеровыми силами инерции ²⁵ (как известно, Л. Эйлер впервые использовал подвижные системы координат для решения сложных задач механики, например сферического движения твёрдого тела). Как даламберовы, так и эйлеровы (и любые) силы инерции не являются физическими, т. е. они нереальны. Вводятся эти несуществующие силы в механику относительного движения, как и в принципе Д'Аламбера, чисто условно - для облегчения решения задач и объяснения отдельных механических явлений.
     Следует заметить, что каждому относительному движению тела, т. е. движению по отношению к выбранной подвижной (неинерциальной) системе отсчёта, соответствует движение некоторого точно такого же тела относительно системы инерциальной, "абсолютной". Чтобы осуществить такое "абсолютное" движение тела, надо воспроизвести не только те же реальные физические силы, которые действовали на исходное тело, но и добавить новые физические силы. Вот эти силы в точности соответствуют эйлеровым силам инерции в данном относительном движении исходного тела. Эйлеровы силы инерции определяются как реальные силы, действующие на тело, в предположении, что подвижная система отсчёта условно принимается за неподвижную. Например, если поворачивающийся автобус условно примем за неподвижный, то те силы, которые мешают нам пройти в нем "по одной доске", приходится считать реальными.
     Во многих случаях неудобно рассматривать движение точек и тел по отношению к "абсолютной" системе координат. Вряд ли имеет смысл развивать теорию колебаний маятника по отношению к "абсолютной", инерциальной системе координат с началом в центре солнечной системы и осями, направленными на неподвижные звёзды. Куда удобнее, и даже естественнее, использовать систему координат с началом в точке подвеса маятника и осями, жестко связанными с Землёй.
     Однако такая система и не "абсолютна", и даже не инерциальна. Земля вращается, а вместе с нею имеет ускорение и центр наших координат - точка подвеса. Как известно, в этом случае ускорение точки в "абсолютной" системе - абсолютное w_a (реальное) ускорение - является векторной суммой трёх ускорений - относительного w_r, переносного w_e и кориолисова w_k:

w_a = w_r + w_e + w_k.

     Относительное ускорение - это ускорение точки в подвижной системе координат, как если бы она была неподвижна. Переносное ускорение - ускорение точки, в данный момент времени совпадающей с рассматриваемой точкой, лежащей в подвижной системе, например связанной с землёй. Кориолисово (...) ускорение, выражаемое как векторное произведение угловой скорости переносного движения ω на относительную скорость v_отн :

w_k = 2[ω × v_отн],                                                      (1.10)

характеризует изменение относительной скорости точки в переносном движении и переносной скорости в относительном движении. Получается так, что если мы складываем два движения: относительное, т. е. движение по отношению к подвижной системе координат (например, Земле), и переносное, т. е. то, с которым сама подвижная система как бы "переносится" в подвижной (например, Земля в "абсолютной" системе отсчёта), то для получения абсолютного (реального) ускорения нам не достаточно просто сложить относительное и переносное ускорение. В этом случае, если подвижная система имеет вращательное движение, а сама точка движется в этой подвижной системе, мы должны ещё прибавить и кориолисово ускорение.
     Таким образом, основное уравнение динамики, или второй закон Ньютона

mw = F                                                                     (1.11)

(сила равна произведению массы на ускорение и направлена так же, как ускорение), для относительного движения будет иметь такой вид:

mw = mw_r - mw_e - mw_k = F + F_e + F_k.                       (1.12)

     Таким образом, основное уравнение динамики относительного движения (1.12) наряду с физической силой F содержит в правой (силовой) части две эйлеровы силы инерции - переносную F_e и кориолисову F_k. И переносная, и кориолисова сила инерции - силы нереальные, их нет на самом деле, зависят они только от выбора конкретной подвижной системы координат и никак не отражают взаимодействий данной материальной точки с другими телами. Не имеют эти силы и противодействия, которое по третьему закону Ньютона должна иметь каждая сила. Следовательно, этот закон равенства и противоположной направленности действия и противодействия никакого отношения к эйлеровым силам не имеет (по образному выражению известного физика Р. Фейнмана, это - псевдосилы).

²⁵ См.: Ишлинский А. Ю. Механика относительного движения и силы инерции, с, 7.»

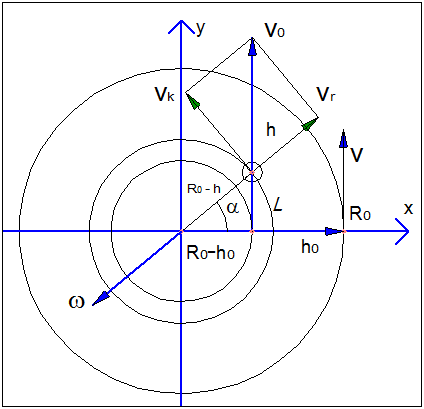
     Проверим на частных примерах, как динамика эйлеровских сил, которая отличается от кинематики только множителем массы, отвечает условиям относительности движения. Для этого, рассмотрим свободное движение (падение) тела внутри центрифуги с кинематической точки зрения. Пусть центрифуга вращается с угловой скоростью ω₀ = const и α – угол отклонения тела от оси x в инерциальной системе отсчёта (x, y), от момента начала свободного движения t = 0; ω = dα/dt – угловая скорость, зависящая от движения тела. Если смотреть из неинерциальной системы отсчёта центрифуги, мы видим, что экспериментатор держит предмет в руке на высоте h₀ и потом отпускает его в момент t = 0. Если смотреть из внешней инерциальной системы (x, y), мы увидим прямолинейное и равномерное движение тела после его отпускания, до момента удара о пол. В этой задаче мы рассматриваем две неинерциальные системы отсчёта, связанные с угловыми скоростями ω₀ и ω.

V₀ = ω₀·(R₀ - h₀) = const – скорость движения тела в инерциальной системе отсчёта в момент отпускания тела. В данном случае движение прямолинейное равномерное; R₀ – радиус пола центрифуги; h₀ – высота, с которой тело начинает свободное падение (движение).

V₀·cos(α) = V_k – окружная скорость тела.

V₀·sin(α) = V_r – радиальная скорость свободного падения тела в центрифуге. Её направление совпадает с радиусом.

V_p = ω₀·(R₀ - h) – переносная скорость наблюдателя, в слое, где тело находится в текущий момент времени:

Дополнительные соотношения:
(R₀ - h)·cos(α) = R₀ - h₀;

L² + (R₀ - h₀)² = (R₀ - h)²;

tg(α) = L/(R₀ - h₀);

V₀·t = (R₀ - h)·sin(α) = L, где L – длинна пройденная телом в инерциальной системе отсчёта;
h – текущая высота тела в центрифуге.

Найдем частоту вращения связанную с движением тела.
tg(α) = L/(R₀ - h₀) дифференцируем это выражение.

ω/cos²(α) = V₀/(R₀ - h₀);

ω = V₀·cos²(α)/(R₀ - h₀) = ω₀·cos²(α), так как V₀/(R₀ - h₀) = ω₀.

ω = ω₀·cos²(α);

Ускорение свободного падения равно:
g_r = dV_r/dt = d(V₀·sin(α))/dt = V₀·ω·cos(α) = ω₀·V₀·cos²(α)·cos(α) =

= ω₀²·(R₀ - h₀)·cos³(α) = ω₀²·(R₀ - h)·cos⁴(α) = ω²·(R₀ - h) = ω·V_k.
Ускорение свободного падения можно правильно связать со структурой центробежной силы только в случае, если, выражать центробежную силу через угловую скорость ω = dα/dt.

g_r = ω²·(R₀ - h).

Обратите внимание, что ускорение g_r может рассматриваться как гироскопическая компонента, что отвечает условиям задачи E = const; dE/dt = 0, так как V₀ = ω₀·(R₀ - h₀) = const в инерциальной системе отсчёта (x, y)
g_r = ω·V_k.

Найдем окружное ускорение тела
g_k = dV_k/dt = d(V₀·cos(α))/dt = -V₀·ω·sin(α) = - ω·V_r.

Найдем окружное ускорение наблюдателя
g_p = dV_p/dt = d(ω₀·(R₀ - h))/dt = - ω₀·dh/dt.

Найдем производную dh/dt через выражение:
L² + (R₀ - h₀)² = (R₀ - h)².

2·L·V₀ = -2·(R₀ - h)·dh/dt;      L·V₀ = - (R₀ - h)·dh/dt.

dh/dt = - L·V₀/(R₀ - h) = - V₀·sin(α) = - V_r.

g_p = ω₀·V_r.

Ускорение дрейфа тела относительно наблюдателя
g_d = g_k + g_p = -ω·V_r + ω₀·V_r = (ω₀ - ω)·V_r =

= (ω₀ - ω₀·cos²(α))·V_r = ω₀·(1 - cos²(α))·V_r = ω₀·sin²(α)·V_r.

Рассмотрим физическую сущность полученных выражений:
g_d = (ω₀ - ω)·V_r. Обратите внимание, что это выражение не может рассматриваться как Кориолисово ускорение.

g_k = - ω·V_r;

g_p = ω₀·V_r;

g_r = ω·V_k.

Определимся со свойствами угловых скоростей ω₀ и ω:
ω – эта угловая скорость непосредственно завязана с движением материальной точки и характеризует интенсивность зависимости ускорения от скорости в относительном движении
g_x = ω·V_y. Её формально можно использовать как кинематическую характеристику тела при движении относительно не инерциальной системы отсчёта. Наличие формальной зависимости силы от скорости в частном случае не означает, что эта сила не удовлетворяет трем законам Ньютона. Центростремительная сила в пределах классической механики является тому хорошим примером. Однако введение этой зависимости в общем случае, без оглядок на соответствие трем законам, уже в явным образом, выводит теорию за пределы классической механики Ньютона. В этом случае начинаются лукавые разговоры о фиктивных силах ... ;

ω₀ – эта угловая скорость наблюдателя в центрифуге. Фактически она влияет только на субъективное восприятие наблюдателём движения и ни как не связана непосредственно с материальной точкой, находящейся в движении по инерции. Эта совершенно абстрактная угловая скорость является базовой в академической механике относительного движения. Её введение обосновывается Гулиа очёнь просто: «Во многих разделах механики и её приложений к техническим наукам движение материальных точек и тел изучается по отношению к подвижным телам большой массы. Движение последних считается практически не зависящим от изучаемого движения сравнительно небольших масс и обычно заранее задаётся.» Фактически за этим текстом стоят определённые ограничения в применении эйлеровской механики относительного движения, которые сформулированы во многих случаях совершенно нечётко. Авторы либо сами не понимают этих ограничений или возможно не утруждают себя разъяснениями по этому поводу (всё равно ничего не поймут ...). Со временем мы разберёмся с этим.

Если рассматривать ускорения, связанные только с материальной точкой, то компоненту
g_p = ω₀·V_r можно не использовать.
Компоненты g_k = - ω·V_r и g_r = ω·V_k удовлетворяют гироскопическому движению

m·g_k·V_k + m·g_r·V_r = - m·ω·V_r·V_k + m·ω·V_k·V_r = 0 и поэтому суммарное ускорение тела можно записать в более общей векторной форме
V₀ = V_r + V_k;     g_n = g_r + g_k.

g_n = -[ω×V₀] – гироскопическое ускорение материальной точки относительно цилиндрической системы координат, записанное через угловую и поступательную скорости, которые наблюдаются в инерциальной системе отсчёта. Фактически это ускорение, которое будет наблюдаться при движении тела относительно цилиндрической системы координат, начало которой совпадает с инерциальной системой отсчёта (x, y) (рассматриваем только плоское движение). Это ускорение можно увидеть и почувствовать, находясь в гипотической центрифуге с угловой скоростью ω на текущей высоте материальной точки в контакте с поверхностью выбранного слоя. Наблюдатель будет регистрировать касательную силу и силу тяжести со стороны поверхности слоя. В "поле" этого ускорения тело падает на дно цилиндрической поверхности. Надо заметить, что это ускорение не более фиктивно, чем Кориолисово, которое тоже обладает гироскопическими свойствами. Такой эффект ускорения появляется из-за разной геометрии, декартовой и цилиндрической систем отсчёта. Обратите внимание, что наблюдатель, находящийся внутри тела, двигаясь ускорено относительно криволинейной неинерциальной системы отсчёта, находится в состоянии невесомости, так как в инерциальной системе отсчёта движется по инерции.
Можно записать в более общем виде, имея в виду, что скорость равна
V = V₀ + ∫a_τ·dt, где скорость и ускорение со направлены, тогда

a = a_τ - [ω×V]. Таким образом, ускорение точки рано сумме тангенциальной и нормальной компоненты ускорения. Это выражение обеспечивает правильную относительность движения тела в инерциальной и неинерциальной цилиндрической системе отсчёта. В инерциальной системе тело движется прямолинейно ускорено, а в неинерциальной с криволинейным ускорением, радиальную компоненту которого можно интерпретировать как центробежное ускорение. ...

Рассмотренные выше расчёты требуют дополнительного пояснения.
Пусть R – радиус вектор материальной точки движущейся относительно инерциальной системы отсчёта. Запишем полную производную от этого радиус-вектора.
V = dR/dt = r·dR/dt + [ω×R], где r – единичный вектор, имеющий направление радиус-вектора,

V = r·V_r + [ω×R] = r·V_r + k·ω·R = r·V_r + k·V_k.

В частном случае при V₀·cos(α) = V_k;   V₀·sin(α) = V_r,

V = r·V₀·sin(α) + k·V₀·cos(α) = V₀·(r·sin(α) + k·cos(α)).

Запишем полное ускорение
a. = v·dV/dt + [ω×V] = r·dV_r/dt + k·dV_k/dt + [ω×V], где v – единичный вектор, имеющий направление вектора скорости; k – единичный вектор перпендикулярный радиус-вектору.

Вычислим [ω×V] = [ω×(r·dR/dt + [ω×R])] = [ω×r]·dR/dt + [ω×[ω×R]] = [ω×r]·V_r - ω²·R =

= k·ω·V_r - ω²·R = k·ω·V_r - r·ω²·R = k·ω·V_r - r·ω·V_k, или

[ω×V] = [ω×(r·V_r + k·V_k)] = [ω×r]·V_r + [ω×k]·V_k = k·ω·V_r - r·ω·V_k, тогда

a. = r·dV_r/dt + k·dV_k/dt + k·ω·V_r - r·ω·V_k;

a. = r·ω·V_k - k·ω·V_r + k·ω·V_r - r·ω·V_k = 0, так как

dV_r/dt = d(V₀·sin(α))/dt = ω·V₀·cos(α) = ω·V_k;

dV_k/dt = d(V₀·cos(α))/dt = -ω·V₀·sin(α) = -ω·V_r.

Полученный результат соответствует условию V₀ = const, так как ускорение постоянного вектора равно нулю. Если снять условие V₀ = const, то

r·dV_r/dt + k·dV_k/dt + [ω×V] = a_τ, т. е. на выходе будет тангенциальная составляющая ускорения.

Обозначим a = r·dV_r/dt + k·dV_k/dt – ускорение относительно неинерциальной системы отсчёта, тогда

a = a_τ - [ω×V].

В случае, когда на тело в неинерциальной системе отсчёта действует произвольная сила, ускорение можно записать так
a = a_τ + a_n - [ω×V], где a_n – ускорение перпендикулярное скорости. a = a_τn - [ω×V].

Рассмотрим случай, когда a_τn = 0, a = - [ω×V]. Пусть V = const в инерциальной системе отсчёта, т. е. тело, движется по инерции. Тогда в неинерциальной системе отсчёта будет наблюдаться гироскопическое движение по закону a = - [ω×V]. Это естественное без силовое движение в неинерциальной системе отсчёта будет подобно движению по инерции. Этот закон определяет траекторию тела движущегося по инерции в неинерциальной системе отсчёта. Например, в центрифуге с маленькой кривизной, тело, брошенное под углом к горизонту, будет двигаться по кривой близкой к параболе. Эта кривая траектория есть результат без силового движения по инерции в неинерциальной системе отсчёта центрифуги. Для изменения этой инерционной траектории к телу необходимо приложить дополнительное ускорение (силу) равное a_τ + a_n. Если тело покоится в неинерциальной системе отсчёта, т. е.
a = a_τ + a_n - [ω×V] = 0, то a_τ = 0, a_n = [ω×V] = - ω²·R. Это значит, что в общем случае мы не можем определить причину искривления траектории тела, т. е. кривизна траектории может быть результат, как относительного движения по инерции, так и силового движения, например, гравитационного. Однако в любом случае мы можем использовать уравнение
a = a_τn - [ω×V]. ...

Движение тела по инерции в инерциальной системе отсчёта и гироскопическое движение этого тела в неинерциальной системе отсчёта математически стыкуются между собой вполне логично и это возможно не случайно. Просто, гироскопическое движение это более общий случай движения по инерции в поле кинематических ускорений, происхождение которых, связано как с относительностью движения, так и с гравитационными полями, которые, по всей видимости, являются просто непонятным для нас относительным неинерциальным движением на уровне других измерений. Тело брошенное к горизонту движется по инерции относительно некоторой 4-системы отсчёта и, вернувшись на землю продолжает своё движение в неинерциальной системе отсчёта земля. Кажущееся изменение скорости тела в процессе падения не более чем изменение проекции 4-скорости в нашем пространстве. В такой интерпретации движения, гравитационные поля просто фикция. Это не значит, что в полевом отношении наше пространство совершенно пустое, просто сама гравитация это не поле. Это вращение пространства в четвёртом измерении. Подобный подход снимает вопрос о скорости распространения гравитации. Сильная гравитация космических объектов обусловлена большой скоростью вращательного движения в 4-измерении и с этим соответственно, связана наблюдаемая энергия поля. Это тоже кинетическая энергия, только спрятанная от нас за ширмой 4-измерения. Такой подход противоречит представлениям о градиенте гравитационного поля. Например, в районе чёрной дыры, где большой градиент тело должно разрывать на части, однако, если гравитация просто относительность движения, то градиентов не должно быть. Вот здесь и работает полевое наполнение пространства, которое тоже движется в относительном вихревом движении, создавая градиенты. Вселенная, образно говоря, гигантский гидродинамический 4-котёл в котором варятся звезды, и гравитация в ней есть просто следствие сложной геометрии пространства наполненного чем-то, что взаимодействует с веществом крайне слабо, либо мы не понимаем сути этого взаимодействия. Рассматривая многомерное пространство необходимо иметь в виду, что это не значит, что реально существует его образ, в человеческом понимании. Многомерность это просто математическое свойство нашего пространства.
   Обратите внимание на математическое построение теории относительности. Вся её суть выражается через понятие интервал, т. е. квадрат расстояния между двумя положениями тела в четырёхмерном пространстве со знаком минус
ds² = -(dx² + dy² + dz² - c²·dt²) = -(dx² + dy² + dz² + i²·(c·dt)²), где i – мнимая единица, которая и определяет свойства дополнительного измерения, в котором мы движемся со скоростью света равной c. Расстояние, которое мы пролетаем в этом измерении равно c·dt. Вся математика теории относительности просто описывает это сложное движение в проекции на наши три измерения. ...

В случае движения тела в сферическом гравитационном поле, уравнение можно интерпретировать так: a = a_τn - [ω×V], где ω – уже вектор угловой скорости ортогональный нашему трехмерному пространству; V – скорость тела в четырёхмерной инерциальной системе отсчёта. Проекцию этой скорости мы и наблюдаем в нашей трехмерной неинерциальной системе отсчёта. Обозначим оси инерциального четырёхмерного пространства через (a, b, e, q). Пусть вектор скорости тела находится только в подпространстве (a, b, e) и V = {V_a, V_b, V_e, 0} = const. Неинерциальная система отсчёта связанная с телом (x, y, z, q) вращается относительно инерциальной системы отсчёта (a, b, e, q) с угловой скоростью ω на плоскости zq. При повороте системы отсчёта (a, b, e) в (x, y, z) скорости преобразуются по закону:

Вокруг zq от x → y

		c	s	0	0	0		×		Va		=		Va·cos(α) + Vb·sin(α)		= {Vx, Vy, 0, 0},
		-s	c	0	0	0				Vb				-Va·sin(α) + Vb·cos(α)
		0	0	0	0	0				Ve				0
		0	0	0	1	0				0				0
		0	0	0	0	1				0				0

где α – угол поворота; s = sin(α); c = cos(α). Вектор скорости относительно неинерциальной системы отсчёта в 4-пространстве равен
{V_x, V_y, 0, 0}. В случае центрального поля плоскость вращения zq касательная к сфере. Непосредственно эту скорость мы наблюдать не можем, так как сами движемся с этой скоростью в 4-пространстве, мы видим только её трёхмерную проекцию. Относительное ускорение, связанное с 4-вращением этой скорости в неинерциальной системе отсчёта воспринимается как гравитация. Центробежное ускорение будет равно,
a_x = -ω·(-V_a·sin(α) + V_b·cos(α));

a_y = ω·(V_a·cos(α) + V_b·sin(α)).

Если ось x направить вверх, а ось y горизонтально, то при α = 0 и V_a = 0 имеем,
g = a_x = -ω·V_b. Относительный угол α для свободно падающего по вертикали тела, всегда равен нулю. ...

Однако против подобного подхода есть серьёзные возражения. ...


   «Гравитационные поля (или поля тяготения) обладают следующим основным свойством: все тела вне зависимости от их массы движутся в них (при заданных начальных условиях) одинаковым образом.
   Например, законы свободного падения в поле тяготения земли одинаковы для всех тел, какой бы массой они ни обладали, – все они приобретают одно и то же ускорение
   Это свойство гравитационных полей даёт возможность установить существенную аналогию между движением тел в гравитационном поле и движением тел, не находящихся в каком-либо внешнем поле, но рассматриваемых с точки зрения неинерциальной системы отсчёта. Действительно в инерциальной системе отсчёта свободное движение всех тел происходит прямолинейно и равномерно, и если, скажем, в начальный момент времени их скорости были одинаковыми, то они будут одинаковыми всё время. Очевидно, поэтому, что если рассматривать это движение в заданной неинерциальной системе, то и относительно неё все тела будут двигаться одинаковым образом.
   Таким образом, свойства движения в неинерциальной системе отсчёта такие же, как в инерциальной системе при наличии гравитационного поля. Другими словами, неинерциальная система отсчёта эквивалентна некоторому гравитационному полю. Это обстоятельство называют принципом эквивалентности. ...
   Однако поля, которым эквивалентны неинерциальные системы отсчёта, всё же не вполне тождественны с "истинными" гравитационными полями, существующими и в инерциальных системах. Между ними имеется существенное отличие в отношении их свойств на бесконечности. На бесконечном расстоянии от создающих поле тел "истинное" гравитационное поле всегда стремится к нулю. Поля же, которым эквивалентны неинерциальные системы отсчёта, на бесконечности, напротив, неограниченно возрастают, или, в крайнем случае, остаются конечными по величине. Так, возникающие во вращающейся системе отсчёта центробежные силы неограниченно растут при удалении от оси вращения; ...
   Поля, которым эквивалентны неинерциальные системы отсчёта, исчезают, как только мы перейдём к инерциальной системе. В противоположность этому, "истинные" гравитационные поля (существующие и в инерциальной системе отсчёта) невозможно исключить никаким выбором системы отсчёта. ... » ст. 288–289.
Л. Д. Ландау., Е. М. Лифшиц. Теоретическая физика том 2., Теория поля. Изд-во "Наука". М., 1973., 504 стр.

А теперь решим задачу "Д в и ж е н и е   м а т е р и а л ь н о й   т о ч к и   в   р а в н о м е р н о   в р а щ а ю щ е й с я   с и с т е м е   к о о р д и н а т." так, как это делается в теории гироскопических систем. Читаем страницу Гироскопические силы. В результате решения появляется Кориолисова сила. Возникает естественный вопрос, почему при рассмотрении движения тела с кинематической точки зрения мы не получили этого результата. Кориолисова сила получается в результате решения задачи с энергетической позиции, через уравнение Лагранжа (возможны другие решения). Это означает, что движение тела должно находится под энергетическим учётом. Тело участвует в передаче и получении энергии при взаимодействии с другими телами, а также энергия тела может меняться при совершении работы центробежной силой. Тогда причём здесь фиктивные силы? Фиктивные силы не могут совершать работу. Если мы решаем задачу с кинематической позиции, то здесь фиктивность сил очевидна и в этом случае нет силы Кориолиса. ...

Рассмотрим неинерциальную систему отсчёта в виде вращающейся арены с угловой скоростью ω₀ и массой m₀ → ∞. Арена абсолютно жесткая. Пусть устройство движется радиально к центру вращения. При таком движении скорость вращения уменьшаться по закону V = ω₀·R и совершается работа против центробежной силы. На устройство так же будет действовать боковая сила. Естественно, что боковая сила зависит от скорости радиального движения, и мы выбираем скорость, при которой не будет проскальзывания опорного механизма. Мы видим, что энергия устройства при движении к центру только уменьшается. Для соблюдения закона сохранения энергии необходимо считать, что энергия передаётся арене. При этом угловая скорость арены будет практически постоянной в силу m₀ → ∞. С формальной точки зрения ясно, что при наличии скорости вращения арены и боковой силы, мощность взаимодействия не равна нулю. Однако, боковая сила, по существу является гироскопической силой Кориолиса и поэтому не может совершать работу по определению. Получается, что гироскопичность силы Кориолиса относительна. С точки зрения наблюдателя на диске гироскопичность соблюдается (он просто не видит передачу энергии), а с точки зрения внешнего наблюдателя нет, так как ему приходится решать вопрос, куда девается энергия. Однако должно быть ясно, что с точки зрения закона сохранения энергии эта относительность не является правильной, так как в основе понятия гироскопичности лежит факт отсутствия передачи мощности, которая не может быть относительной. Эта двойственность проявляется даже в книгах по гироскопам. Некоторые авторы запросто пишут о том, что сила Кориолиса вызывает деформации упругих элементов гироскопа, не задумываясь над тем, как гироскопическая сила может передать энергию для деформации упругого элемента, если она по математическому происхождению не может совершать работу. Подобная странная ситуация указывает на то, что наши воззрения на механическое движение в чём-то весьма непоследовательны.

Многие теоретики из подобной ситуации выходят очень просто, считают силы инерции фиктивными и соответственно в этом случае о законе сохранения энергии можно и не вспоминать, а в тех случаях, когда реальность сил очень трудно отрицать, можно лукаво сказать: «Эйлеровы силы инерции определяются как реальные силы, действующие на тело, в предположении, что подвижная система отсчёта условно принимается за неподвижную. Например, если поворачивающийся автобус условно примем за неподвижный, то те силы, которые мешают нам пройти в нем "по одной доске", приходится считать реальными». При этом силы инерции вычисляются из энергетических соображений, через кинетическую энергию и уравнение Лагранжа, но они не реальны и третий закон на них не распространяется и соответственно неважно, что происходит с энергией. Образно говоря, процветает полная энергетическая бесхозяйственность. Вместо того чтобы разобраться в реальных энергетических процессах в неинерциальных системах, искусственно ввели фиктивные силы инерции. К сожалению многие теоретики, которые пошли путём фиктивных сил, не понимают, что фактически встали на путь нарушения закона сохранения энергии. ...

Оглавление

Продолжение