| |
«§ 23. Силы Кориолиса. Покажем, что во вращающейся системе на тело, перемещающееся относительно этой системы, действует, кроме центробежной силы, ещё добавочная сила. Эта сила, носящая название кориолисовой силы (в честь французского математика Кориолиса, \(1795-1843\) ), зависит от скорости v′ тела относительно вращающейся системы и от угловой скорости вращения системы \(ω\).
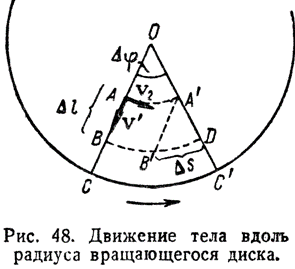
Рассмотрим сперва частный случай. Пусть система представляет собою диск, вращающийся с постоянной угловой скоростью \(ω\) вокруг вертикальной оси \(O\) (рис. 48) в направлении, указанном стрелкой. Пусть тело a перемещается равномерно из точки \(A\) вдоль радиуса \(OC\) со скоростью \(v^{~′}\) относительно диска. За время \(Δt\) тело a пройдёт отрезок \(Δl= AB =v^{~′} Δt\). За это время \(Δt\) в неподвижной системе координат радиус \(OC\), благодаря вращению диска, повернётся на угол \(Δ φ = ω ~Δ l\), и тело передвинется из \(A\) в \(D\). В неподвижной системе координат тело a принимает одновременно участие в двух движениях: в движении относительно диска со скоростью \(v^{~′}\) и в движении вместе со вращающимся диском. Линейная скорость вращения диска различна для различных мест диска. Обозначим её значение в точке \(A\) через \(v_r\). Двигаясь лишь со скоростью вращения \(v_r\), тело a описало бы дугу \(\breve{AA^{′}}\) и пришло бы в точку \(A^{′}\). Двигаясь одновременно со скоростью \(v_r\) и относительной скоростью \(v^{~′}\), тело a должно было бы попасть в точку \(B^{~\prime}\) (отрезок \(A^{~\prime} B^{~\prime}||AB\)). На самом деле тело a переходит в точку \(D\). Это происходит за счёт того, что линейная скорость вращения \(v_r\) возрастает по мере удаления точки a от центра вращения. Таким образом, относительно неподвижной системы координат тело a, двигаясь вдоль радиуса, непрерывно меняет свою скорость: оно движется ускорено. Величина этого ускорения \(w\) может быть определена по тому добавочному пути
\(\breve{Δ s}= \breve{B^{~′} D}\), который тело a прошло за время \(Δt\). Из рис. 48 имеем:
\(Δs = A^{\prime} B^{~\prime} Δφ\),
или, так как \(A^{\prime} B^{~\prime}= Δl= v^{~\prime} Δt\) и \(Δφ= ω Δt\), то:
\(Δ s= ω v^{~′} \left(Δ t \right)^2\). \(~~~~~~~~\) (1)
\(~~~~\) Следовательно, добавочный путь \(Δs\) возрастает пропорционально квадрату времени \(Δt\). Но пропорциональность пути квадрату времени \(Δt\) имеет место при движении с постоянным ускорением (равномерно-ускоренном движении), при котором:
\(Δ s= \frac{1}{2} w \left(Δ t \right)^2\).
\(~~~~\) Сравнивая это выражение для
\(Δs\) с (1), получим, что тело a испытывает ускорение:
\(~~~~~~~~~~~~~~~~~~~~~w= 2v^{~′} ω\). \(~~~~~~~~~~~~~~~~~~~\) (2)
\(~~~~\) Это ускорение направлено перпендикулярно к относительной скорости \(v^{~′}\), и в нашем случае - направо. Для того чтобы сообщить телу a это ускорение, к нему необходимо приложить силу \(f\), направленную направо и равную \(f = mw\), где \(m~-\) масса тела. Не будь силы \(f\), тело отклонилось бы во вращающейся вместе с диском системе координат от своего "прямолинейного" движения вдоль радиуса диска.
\(~~~~\) Сила \(f_k\) равная силе \(f\), но направленная в противоположную сторону, будет действовать по третьему закону Ньютона на те связи, которые удерживают тело a при его движении на радиусе. Совершенно аналогично, как в ранее рассмотренных случаях ускоренных систем, пользуясь координатной системой, вращающейся вместе с диском, будем считать, что сила \(f_k\) приложена к самому телу a.
Таким образом, во вращающейся системе к телу, движущемуся вдоль радиуса со скоростью \(v^{~′}\), приложена "инерционная" сила:
\(f_k= 2v^{~′} ω m\), \(~~~~~~~~~~~~\) (3)
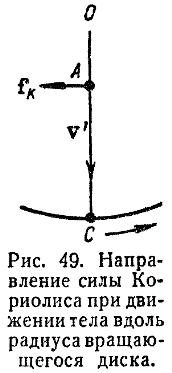
направленная перпендикулярно к \(v^{~′}\) (в нашем примере налево, см. рис. 49).
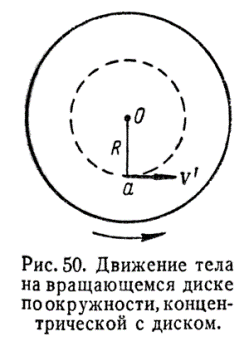
Сила \(f_k\) и носит название силы Кориолиса. Покажем теперь, что сила Кориолиса существует и в том случае, когда тело a движется на диске по окружности с центром на оси вращения (рис. 50). При движении тела a относительно диска со скоростью \(v^{~′}\) полная скорость в неподвижной системе координат равна \(v_r + v^{~′}\), где \(v_r-\) линейная скорость вращения диска в том месте, где находится тело a. Следовательно, на тело a действует центростремительная сила:
\(\displaystyle f_ц= \frac{m(v_r+ v^{~′})^2}{R}\),
где \(R~-\) расстояние от оси вращения до тела. Возводя в этой формуле сумму \((v_r+ v^{~′})\) в квадрат, получим:
\(\displaystyle f_ц= \frac{m v_r^2}{R}+ \frac{m {v^{~′}}^2}{R}+ \frac{2m v^{~′} v_r}{R}\).
\(~~~~\) В координатной системе, связанной с диском, член
\(\displaystyle \frac{m v_r^2}{R}\) определяет инерционную центробежную силу, вызванную вращением диска с угловой скоростью \(ω\); член
\(\displaystyle \frac{m {v^{~\prime}}^2}{R}\) определяет центробежную силу, вызванную относительным движением тела по кругу радиуса \(R\) со скоростью \(v^{~\prime}\); член
\(\displaystyle f= \frac{2m v^{~\prime} v_r}{R} = 2m v^{~\prime} ω\)
определяет добавочную силу, вызванную одновременным наличием как вращения диска, так и движения тела относительно диска.
\(~~~~\) Сила \(f_k\), равная силе \(f\), но направленная в противоположную сторону, даст для этого случая силу Кориолиса.
\(~~~~\) Эта сила совпадает по величине с силой, возникающей при движении вдоль радиуса [формула (3)], и направлена также перпендикулярно к относительной скорости.
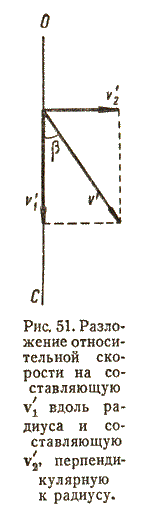
\(~~~~\) Теперь рассмотрим случай, когда тело a движется с относительной скоростью v,, направление которой составляет угол \(β\) с радиусом \(OC\) (рис. 51).
\(~~~~\) В этом случае скорость v, можно разложить на две составляющие: на составляющую вдоль радиуса v,1 = v, cos β и составляющую перпендикулярную к радиусу, v,2 = v, sin β.
\(~~~~\) Составляющей v,1 по формуле (3) соответствует кориолисова сила
fk1 = 2v, ω cos β · m, составляющей v,2 - сила fk2 = 2v, ω sin β · m,
полная сила Кориолиса:
fk = √(f 2k1 + f 2k2) = 2v, ωm.
\(~~~~\) Таким образом, и для произвольного направления относительной скорости v, для силы Кориолиса сохраняется выражение (3).
\(~~~~\) Наконец, рассмотрим самый общий случай, когда тело движется в направлении, составляющем угол \(α\) с осью вращения (рис. 52). Тогда разложим скорость v, на составляющую v,1, перпендикулярную к оси вращения, и составляющую v,2, параллельную оси вращения. Эта последняя составляющая не обуславливает никакого изменения расстояния от оси и, следовательно, не может вести к появлению добавочных ускорений и сил. Отсюда величина силы Кориолиса определяется лишь составляющей v,1 = v, sin α. Заменяя в формуле (3) v, через v,1 = v, sin α, получим общее выражение для силы Кориолиса:
fk = 2v, ω sin α · m. \(~~~~~~~~~~~~~~~~\)(4)
\(~~~~\) Во всех случаях сила Кориолиса направлена перпендикулярно и к переносной скорости v, и к оси вращения. Для определения направления силы fk введём в рассмотрение вектор угловой скорости ω (см. § 12а). Тогда кориолисова сила \(f_k\) направлена перпендикулярно к плоскости, содержащей векторы ω и v, (рис. 53), и так, что если сопоставить направление поворота головки буравчика от вектора v, к вектору ω (в направлении меньшего угла), то направление силы \(f_k\) определится направлением поступательного движения буравчика.
\(~~~~\) Если воспользоваться обозначениями векторного анализа, то \(f_k\) определится через векторное произведение векторов v, и ω (см. § 12а):
fk = 2[v, × ω] \(m\).
\(~~~~~~~~~~~~~~~~~~~~\)(4а)
\(~~~~\) Сила Кориолиса проявляется при движениях по поверхности земного шара, обладающего определённой угловой скоростью, благодаря суточному вращению. Предположим, например, что поезд идёт в северном полушарии в меридиональном направлении на север (точка а на рис. 54). При этом вектор относительной скорости v, составляет острый угол α с вектором угловой скорости ω, и кориолисова сила \(f_k\) направлена касательно к земной поверхности направо, если встать лицом по ходу движения поезда. Поезд оказывает на правый рельс большее давление, чем на левый. В южном полушарии, при движении поезда к югу (точка а, на рис. 54), v, составит с ω тупой угол, и сила Кориолиса направлена налево относительно хода движения. Существованием силы Кориолиса объясняются подмывание реками в северном полушарии правого, а в южном - левого берегов (закон Бера), возникновение северо-восточных пассатов в северном полушарии и т. д.
\(~~~~\) Другим примером влияния сил Кориолиса на движение тел у поверхности земного шара являются: отклонение свободно падающих тел к востоку от вертикали и отклонение плоскости качаний маятника. Разберём последний случай несколько подробнее. Предположим для простоты, что маятник совершает колебания на северном полюсе. Тогда скорость груза маятника v, всё время перпендикулярна к оси земного шара (при большой длине нити) и, следовательно, v, ⊥ ω, где ω - по-прежнему вектор угловой скорости вращения Земли. В результате на груз маятника действует сила Кориолиса, численно равная fk = 2mv,ω, лежащая в горизонтальной плоскости и направленная в право по отношению к вектору v,. Под действием этой силы груз маятника при каждом размахе отклоняется в право. В результате, плоскость качаний маятника будет поворачиваться относительно Земли в направлении часовой стрелки и повернётся на угол \(2π\) за сутки. В случае качаний маятника на широте \(φ\) плоскость качаний повернётся в сутки на угол \(2π~sin~φ\). Наблюдение отклонения плоскости качаний маятника было впервые проведено Фуко в 1851 г. и послужило прямым доказательством существования суточного вращения Земли.»
С. Э. Фриш и А. В. Тиморева., Курс общей физики, Том 1, "Гос. изд. Технико-теоретической лит.", Москва 1953, ст. 74 - 78.
\(~~~~\) То, что маятник повернётся на \(2π\) за сутки нет сомнения, так как с точки зрения относительного движения, маятник не меняет своей плоскости качания, а под ним просто крутится земля. А вот будет ли расчёт, сделанный на основании формулы \(f_k= 2mv^{~\prime} ω\) соответствовать этому факту стоит проверить и сделать это несложно. Ответим на вопрос, какая относительная скорость вращения маятника относительно земли?
Ответ простой: \(v_k= ω \cdot s^{~\prime}\), где \(s^{~\prime}~-\) отклонение маятника от оси вращения земли; \(v_k~-\) скорость относительного вращения. Это справедливо для любой точки траектории, исходя из относительности движения. Для обеспечения колебаний маятника в одной плоскости будем считать, что исходное положение маятника совпадало с осью, и в результате внешнего импульса он пришёл в движение. Обратите внимание, что возможен и другой режим движения маятника, который получается, если первоначально его отклонить от вертикали и отпустить. В этом случае маятник имеет не нулевую начальную окружную скорость и будет отклоняться от оси вращения земли. В неподвижной системе отсчёта его траектория будет эллиптической, т. е. колебания будут происходить уже в двух плоскостях.
Запишем ускорение под действием силы Кориолиса, разделив силу на массу маятника
\(\vec a_k= 2\left[\left(\vec v^{~\prime} + \vec v_r \right) \times \vec \omega \right] \approx 2\left[\vec v^{~\prime} \times \vec \omega \right]\). Выполняется с достаточной точностью рядом с осью вращения, где \(v^{~\prime} \gg v_r\).
\(a_k= 2v^{~\prime} ω\). Проинтегрируем это выражение по времени и найдем скорость \(v_k\). Отсчёт времени от момента пересечения оси вращения земли.
\(\displaystyle v_k= \int_0^{t} a_k~ dt= \int_0^{t} 2v^{~\prime} ω dt= 2ω \int_0^{t} v^{~\prime} dt\).
Так как \(\displaystyle \int_0^{t} v^{~\prime} dt= s^{~\prime}\), то будет
\(v_k= 2ω s^{~\prime}\).
Таким образом, если исходить из ускорения Кориолиса, то скорость относительного вращения маятника в каждой точке траектории будет в два раза больше, чем следует из относительного расчёта, что не может быть в принципе. Сила Кориолиса в этом случае явно даёт неправильный результат. Обратите внимание, что если маятник выполнить в виде желоба (закреплённого на земле) по которому катится шар, то на шар будет действовать именно сила Кориолиса, в точности по уравнению \(f_k= 2mv^{~\prime} ω\). Причина такого не соответствия силы и реального ускорения объясняется просто, формула для силы кориолиса соблюдается только, если тело жестко привязано к поверхности диска в окружном направлении и может свободно двигаться в радиальном направлении. Для свободного маятника в этой задаче, формула силы Кориолиса не подходит.
Естественно появляется вопрос, почему в других задачах всё сходится.
Например, рассмотрим задачу из учебника Арнольда В. И., «Математические методы классической механики».
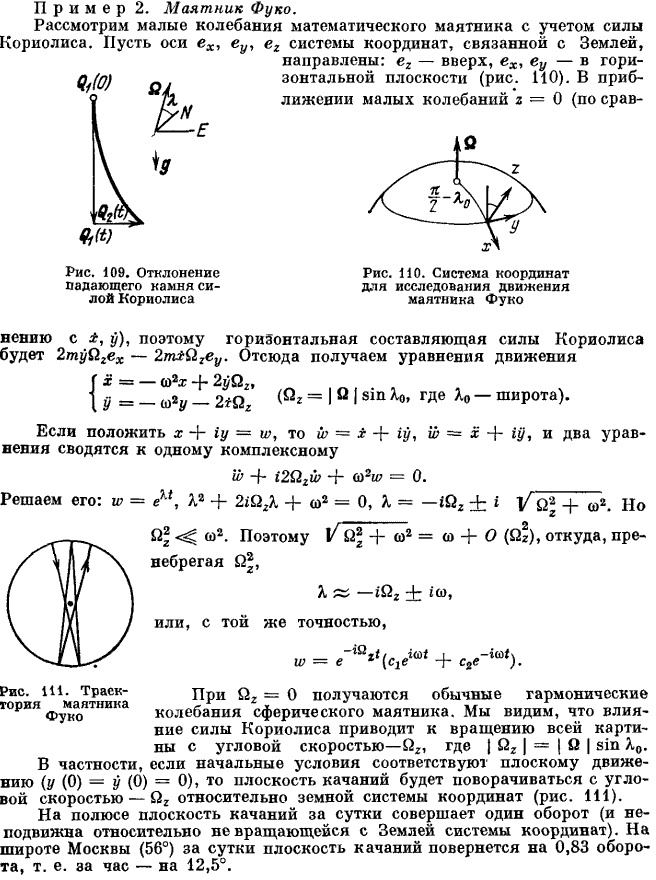
Для начала кратко повторим этот пример, в более точном варианте. Для этого используем полное дифференциальное уравнение при \(Ω_z=const\).
\(\vec a=-ω^2 \vec r -2\left[\vec \Omega_z \times \vec v \right] + Ω_z^2 \vec r\). Тогда в комплексном виде можно записать
\(\ddot{w} + i2Ω_z \dot{w} + (ω^2- Ω_z^2) w=0\).
\(\lambda^2 + i2Ω_z \lambda + (ω^2- Ω_z^2)=0\).
\(\displaystyle \lambda = \frac{-i2Ω_z \pm \sqrt{-4Ω_z^2 - 4(ω^2 -Ω_z^2)}}{2}= -iΩ_z \pm iω\).
Видно, что решение получается точное. Член уравнения, которым пренебрёг Арнольд с точки зрения точности решения не имеет значения.
Однако с теоретической точки зрения очень важен, пренебрежение им утверждает силу Кориолиса, а его сохранение выводит на другой уровень понимания принципа действия сил инерции.
Рассмотрим уравнение \(\vec a=-ω^2 \vec r -2\left[\vec \Omega_z \times \vec v \right] + Ω_z^2 \vec r~~\) в частном случае, когда маятник в момент начала движения находится в крайнем положении и покоится.
Перепишем его в другом виде
\(\vec a=-ω^2 \vec r -\left[\vec \Omega_z \times (\vec v_{a} - [\vec Ω_z \times \vec r] ) \right] -\left[\vec \Omega_z \times \vec v \right] + Ω_z^2 \vec r\).
\(\vec a=\left(-ω^2 \vec r -\left[\vec \Omega_z \times \vec v_{a} \right] \right) -\left[\vec \Omega_z \times \vec v \right]\).
В этом уравнении гироскопическим является только слагаемое \(-\left[\vec \Omega_z \times \vec v \right]\).
Сумма \( -ω^2 \vec r -\left[\vec \Omega_z \times \vec v_{a} \right]\) является тангенциальным ускорением на траектории движения маятника в не ИСО.
\(\vec v_{a}~-\) вектор скорости маятника в неподвижной системе отсчёта.
Это значит, что физически гироскопической силы Кориолиса в этом случае не существует.
В качестве доказательства можно вычислить угловую скорость вращения вектора скорости на траектории, \(\Omega_z\).
\(\displaystyle r=e^{-i\Omega_z t} \left(c_1 e^{i \omega t} + c_2 e^{-i \omega t} \right)\).
Определимся с начальными условиями для этого случая
\(\displaystyle c_1 e^{i \omega t} + c_2 e^{-i \omega t}= (c_1+c_2)cos(\omega t) + i(c_1-c_2)sin(\omega t)= a~cos(\omega t) + i~b~sin(\omega t)\).
\(\displaystyle r=e^{-i\Omega_z t} \left( a~cos(\omega t) + i~b~sin(\omega t) \right)\), при \(\omega b=\Omega_z a\).
Радиус кривизны траектории равен \(\displaystyle R=\frac{ (\dot{r} \cdot \bar{\dot{r}})^{3/2} }{Im( \bar{\dot{r}} \cdot \ddot{r})}\).
Угловая скорость равна \(\displaystyle \Omega=- \frac{Im(\bar{\dot{r}} \cdot \ddot{r})}{\dot{r} \cdot \bar{\dot{r}}}= \Omega_z\).
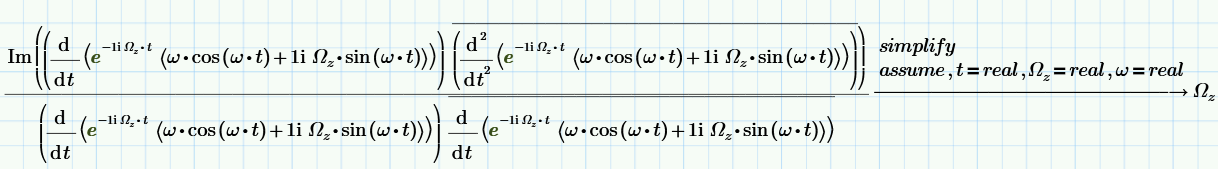
Скалярное произведение \(\left(-ω^2 \vec r -\left[\vec \Omega_z \times \vec v \right] + Ω_z^2 \vec r \right) \cdot \left[\vec \Omega_z \times \vec v \right]=0\). Тангенциальное ускорение из суммы выделено правильно.
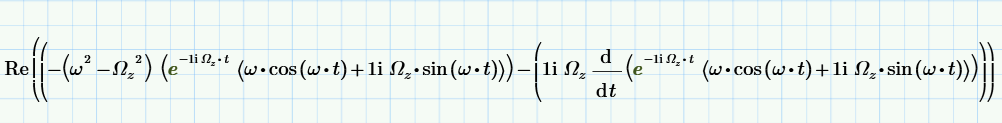
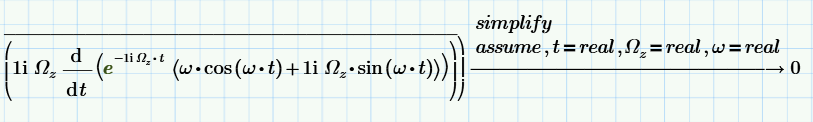
Траектория маятника при выбранных начальных параметрах.
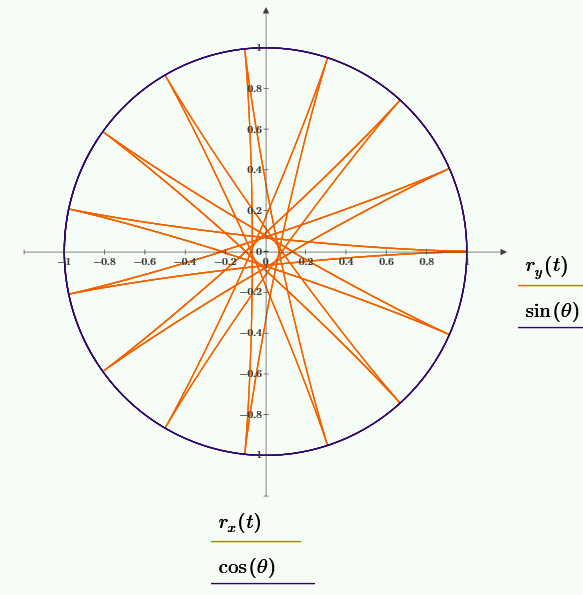
Закон сохранения энергии.
\(\displaystyle \frac{v^2}{2}+ \frac{1}{2} (ω^2- Ω_z^2) \cdot r^2 = const\).
Обратите внимание, что в уравнении присутствует потенциал не инерциальной системы отсчёта \(-\frac{1}{2} Ω_z^2 \cdot r^2\).
У Арнольда закон сохранения энергии в условии задачи не учтён.
...

Решая эту задачу будем считать, что ось \(x\) является действительной и проходит вертикально в шахте через центр Земли. Ось \(y\) мнимая и касательна параллели.
Запишем дифференциальное уравнение закона движения камня в центральном гравитационном поле вращающегося тела.
\(\displaystyle \vec a=-\left(\frac{GM}{r^3} \right) \vec r -2\left[\vec \Omega_z \times \vec v \right] - \left[\vec Ω_z \times \left[\vec Ω_z \times \vec r \right ] \right]\).
Для плоскости экватора
\(\displaystyle \vec a=-\left(\frac{GM}{r^3} \right) \vec r -2\left[\vec \Omega_z \times \vec v \right] + Ω_z^2 \vec r\).
Делаем замену переменной \(\vec r\).
\(\vec r = \vec R + \vec r_1\); \(~~\vec v = \vec v_1\).
\(\vec R~-\) постоянный вектор, соединяющий центр Земли и дно шахты.
\(\vec r_1~-\) радиус-вектор камня, исходящий из центра дна шахты.
\(\displaystyle \vec a=-\left(\frac{GM}{{|\vec R+ \vec r_1|}^3} \right) (\vec R + \vec r_1) -2\left[\vec \Omega_z \times \vec v_1 \right] + Ω_z^2 (\vec R + \vec r_1)\).
\(\displaystyle \vec a=-\left(\frac{GM}{{|\vec R+ \vec r_1|}^3} \right) \vec r_1 -2\left[\vec \Omega_z \times \vec v_1 \right] + Ω_z^2 \vec r_1 - \left(\frac{GM}{{|\vec R + \vec r_1|}^3} \right) \vec R + Ω_z^2 \vec R\).
\(\displaystyle \vec a=-\left(\frac{GM}{R^3} \right) \vec r_1 -2\left[\vec \Omega_z \times \vec v_1 \right] + Ω_z^2 \vec r_1 - \left(\frac{GM}{R^3} \right) \vec R + Ω_z^2 \vec R\).
В этом случае относительная погрешность по \(r_1\) будет меньше чем \(\displaystyle \left(\frac{R+h}{R} \right)^3 - 1 = 0,000118\).
\(\displaystyle \vec a=-\left(\frac{g}{R} \right) \vec r_1 -2\left[\vec \Omega_z \times \vec v_1 \right] +Ω_z^2 \vec r_1 -\left(\frac{g}{R} \right) \vec R + Ω_z^2 \vec R\).
\(\displaystyle ω= \sqrt{\frac{g}{R}}\); \(\displaystyle ~~T_ш= \frac{2 \pi}{\omega} \equiv 84,4~минуты~-\) период Шулера, используется в навигации.
\(\displaystyle \vec a=-ω^2 \vec r_1 -2\left[\vec \Omega_z \times \vec v_1 \right] +Ω_z^2 \vec r_1 -ω^2 \vec R + Ω_z^2 \vec R\).
Убираем индекс при радиус-векторе.
\(\displaystyle \vec a=-(ω^2 -Ω_z^2) \vec r -2\left[\vec \Omega_z \times \vec v \right] -(ω^2 -Ω_z^2) \vec R\).
Записываем решение для плоскости экватора в комплексном виде, используя ранее полученный результат.
\(\displaystyle r=e^{-i\Omega_z t} \left(a~cos(\omega t) + i~b~sin(\omega t) \right) -\frac{1}{2} \left(g- Ω_z^2 R \right)~t^2\).
\(v(0)= \omega b -\Omega_z a = \Omega_z h\); \(~~a=h\) и с учётом широты
\(\displaystyle r=h~e^{-i\Omega_z t} \left(cos(\omega t)+ i \frac{2 \Omega_z}{\omega} sin(\omega t) \right)cos(\lambda) -\frac{1}{2} \left(g- Ω_z^2 R \right)cos(\lambda)~t^2\).
\(R=6371000~м\); \(~~g=9,80665~м/с^2\); \(~~\lambda = 60 °\) \(~~ Ω_z= \frac{2 \pi}{24 \cdot 60 \cdot 60} \approx 7,272 \cdot 10^{-5}\); \(~~h=250~м\).
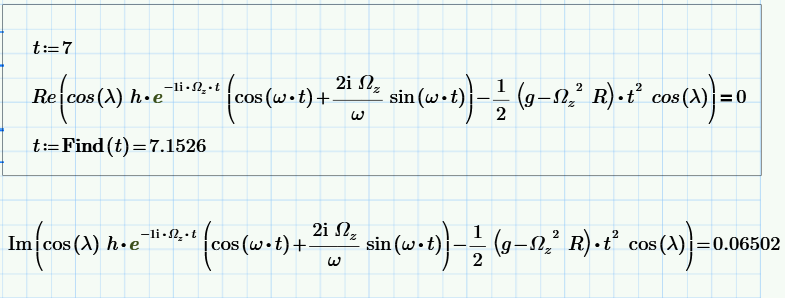
Сделаем простую проверку правильности решения.
Рассмотрим задачу с точки зрения относительности движения. За время падения камня на дно шахты Земля повернётся на угол \(\Delta \phi = \Omega_z t\).
Разность расстояний между дном и поверхностью с учётом широты равна \(\Delta l = \Delta \phi ~ h ~ cos(\lambda)\).
Поэтому \(\Delta l =t~ h~ \Omega_z~ cos(\lambda)= 6,5019~см\).
Если взять время падения из \(\sqrt{\frac{2h}{g}}\), тогда \(\Delta l=6,491~см\).
Погрешность вносимая ошибкой при вычислении времени падения незначительна.
Поэтому в решении Арнольда ошибка на множитель \(\frac{2}{3}\) появляется в результате интегрирования силы Кориолиса, т.е. в силе Кориолиса
вместо двойки надо поставить тройку, чтобы получить правильное решение по Арнольду.
...
Рассмотрим более общий случай движения маятника Фуко при \(v(0)= \omega b -\Omega_z a \neq 0\), в этом случае угловая скорость на траектории уже не равна \(\Omega_z\).
К уравнению \(\displaystyle \vec a=-(ω^2 -Ω_z^2) \vec r -2\left[\vec \Omega_z \times \vec v \right]\) надо добавить уравнение
\(\displaystyle \left[\vec \Omega_{zd} \times \vec v \right] - \left[\vec \Omega_{zd} \times \vec v \right]=0\), где \(\Omega_{zd}~-\) дополнительная угловая скорость,
зависящая от параметров, начальных условий и скорости.
\(\displaystyle \vec a= \left\{-(ω^2 -Ω_z^2) \vec r -\left[(\vec \Omega_z- \vec \Omega_{zd}) \times \vec v \right] \right\} -\left[(\vec \Omega_z + \vec \Omega_{zd}) \times \vec v \right]\). В фигурных скобках тангенциальное ускорение.
\(\displaystyle \vec \Omega_{zd}= \frac{\vec P_z}{v^2}\); \(~~\vec P_z = \vec {const}\).
\(\vec P_z = \left[ \left(-(ω^2 -Ω_z^2) \vec r -\left[\vec \Omega_z \times \vec v \right] \right) \times \vec v \right]= \vec k \cdot ω~ v(0)~ v(T/4)\).
\(v(T/4)= \Omega_z b - \omega a~-\) максимальная скорость.
\(v(0)= \omega b -\Omega_z a~-\) минимальная скорость.
...
Подобная ситуация показывает, что сложившийся стереотипный догмат в использовании силы Кориолиса имеет крайне большую силу. Многие весьма серьёзные и уважаемые учёные совершенно бездумно, поддерживают эту не допустимую ситуацию.
Рассматривая подобные задачи, надо помнить, что формула силы Кориолиса всегда выдаёт значение силы, которое необходимо приложить к телу с противоположным знаком со стороны других тел системы, чтобы во вращающейся системе отсчёта оно двигалось по инерции. Например, если поднимать тело с постоянной скоростью вдоль радиуса центрифуги, вращающейся по часовой стрелке, то для наблюдателя стоящего на полу центробежная сила будет направлена книзу, а сила Кориолиса в направлении вращения. Для реализации подобного движения к телу необходимо приложить противоположные силы, исходящие от подъёмного устройства. Если силы, приложенные со стороны подъёмного устройства не равны силе Кориолиса, то тело будет ускоряться во вращающейся системе отсчёта.
Обратите внимание, что когда тело начинает двигаться в окружном направлении, то его угловая скорость фактически меняется, на что совершенно не обращают внимания и включают окружную скорость в уравнение силы Кориолиса при неизменной частоте вращения. Между тем, правильная угловая скорость вращения тела может определятся только радиус вектором, связанным с инерциальной системой отсчёта. К сожалению эта вроде бы простая истина игнорируется в угоду традиционного подхода обусловленного математической конструкцией силы Кориолиса физически ограниченной в применении.
fц = m(vr + v,)2/R = mvr2/R + mv, 2/R + 2m·v,·vr/R = m·ωR2·R, где ωR – угловая скорость радиус вектора. Поэтому радиальная компонента силы Кориолиса обнуляется при замене угловой скорости ω на ωR, так как полностью входит в центростремительную силу.
Задача на движение тела в не инерциальной системе отсчёта.
Пусть в ИСО из начала координат движется тело с постоянной радиальной скоростью vr. Угловая скорость вращения не ИСО равна Ω. Вращение происходит против часовой стрелки. Вектор угловой скорости по правилу правого буравчика направлен от циферблата часов. Наблюдатель, находится в не ИСО. Найдём скорость движения тела в не ИСО и дифференциальное уравнение для ускорения тела.
Координаты тела в инерциальной системе отсчёта равны
Rx = vr·cos(φ0)·t;
Ry = vr·sin(φ0)·t, где vr — модуль радиальной скорости; φ0 — угол, определяющий направления движения тела; t — время.
Закон вращения в не ИСО можно записать так
\(~~~~~~~\) rx = Rx·cos(Ω·t) + Ry·sin(Ω·t);
\(~~~~~~\) ry = -Rx·sin(Ω·t) + Ry·cos(Ω·t).
\(~~~~~~\) rx = vr·cos(φ0)·t·cos(Ω·t) + vr·sin(φ0)·t·sin(Ω·t);
\(~~~~~~\) ry = -vr·cos(φ0)·t·sin(Ω·t) + vr·sin(φ0)·t·cos(Ω·t).
rx = (cos(Ω·t)·cos(φ0) + sin(Ω·t)·sin(φ0))·vr·t;
ry = (cos(Ω·t)·sin(φ0) - sin(Ω·t)·cos(φ0))·vr·t.
\(~~~~~~~\) rx = vr·cos(Ω·t - φ0)·t = vrx·t;
\(~~~~~~~\) ry = -vr·sin(Ω·t - φ0)·t = vry·t.
Векторном виде
r = vr·t (0).
Дифференцируем координаты по времени
vx = -vr·Ω·sin(Ω·t - φ0)·t + vr·cos(Ω·t - φ0);
vy = -vr·Ω·cos(Ω·t - φ0)·t - vr·sin(Ω·t - φ0).
\(~~~~~~~\) vx = Ω·ry + vr·cos(Ω·t - φ0) = Ω·ry + vrx;
\(~~~~~~~\) vy = -Ω·rx - vr·sin(Ω·t - φ0) = -Ω·rx + vry.
В векторном виде
v = -[Ω×r] + vr (1), где -[Ω×r] — скорость вращения радиус-вектора тела; vr — поступательная радиальная скорость тела. Указанные составляющие ортогональны. Относительная скорость вращения тела по модулю равна Ω·r.
Полученное уравнение физически корректно. Для маятника этим способом, можно получить аналогичное уравнение.
Вычислим (1) из (0)
v = dr/dt = d(vr·t)/dt = (dvr/dt)·t + vr = (r/r)·(dvr/dt)·t - [Ω×vr]·t + vr = -[Ω×(vr·t)] + vr = -[Ω×r] + vr. При dvr/dt = 0.
Вычислим ускорение, дифференцируя скорость
\(~~~~~~~\) ax = -vr·Ω2·cos(Ω·t - φ0)·t - vr·Ω·sin(Ω·t - φ0) - vr·Ω·sin(Ω·t - φ0);
\(~~~~~~~\) ay = vr·Ω2·sin(Ω·t - φ0)·t - vr·Ω·cos(Ω·t - φ0) - vr·Ω·cos(Ω·t - φ0).
ax = -vr·Ω2·cos(Ω·t - φ0)·t - vr·Ω·sin(Ω·t - φ0) - vr·Ω·sin(Ω·t - φ0) + (- vr·Ω2·cos(Ω·t - φ0)·t + vr·Ω2·cos(Ω·t - φ0)·t );
ay = vr·Ω2·sin(Ω·t - φ0)·t - vr·Ω·cos(Ω·t - φ0) - vr·Ω·cos(Ω·t - φ0) + ( vr·Ω2·sin(Ω·t - φ0)·t - vr·Ω2·sin(Ω·t - φ0)·t ).
\(~~~~~~~\) ax = 2·Ω·vy + Ω2·rx;
\(~~~~~~~\) ay = -2·Ω·vx + Ω2·ry.
В векторном виде
a = -2·[Ω×v] + Ω2·r (2).
Получим это дифференциальное уравнение непосредственно из v = -[Ω×r] + vr.
a = dv/dt = -d[Ω×r]/dt + dvr/dt = -[Ω×dr/dt] + dvr/dt = -[Ω×v] + (r/r)·dvr/dt - [Ω×vr] = -[Ω×v] - [Ω×vr], так как dvr/dt = 0, модуль радиальной скорости по условию задачи постоянный.
Обратите внимание, что из (1) следует v = -ve + vr; vr = v + ve, где ve = [Ω×r] — скорость вращения радиус-вектора.
a = -[Ω×v] - [Ω×(v + ve)] = -2·[Ω×v] - [Ω×ve] = -2·[Ω×v] - [Ω×[Ω×r]] = -2·[Ω×v] + Ω2·r.
Из этого видно, что удвоение при ускорении Кориолиса есть следствие дифференцирования вектора радиальной поступательной скорости
dvr/dt = (r/r)·dvr/dt - [Ω×vr]. Вектор радиальной скорости вращается в не ИСО, и поэтому физически нет основания дифференцировать его по-другому, а значит уравнение (2) физически работает правильно. Тело движется в градиенте окружной скорости, создаваемой вращением. Проблемы в применении ускорения Кориолиса не связаны с физическими ошибками в уравнениях подобных (2). Проблема в том, что ускорение Кориолиса и центробежная сила не являются не зависимыми силовыми компонентами и поэтому их использовать в общем случае по отдельности, нельзя. Необходимо решать уравнение в полном комплекте. Выделение ускорения Кориолиса из уравнения как физически обусловленной формулы, является принципиальной теоретической ошибкой, и эта ошибка заложена в учебниках.
Уравнение (2) не поддерживает закон сохранения энергии. Тело при удалении от начала координат неограниченно увеличивает свою скорость в не ИСО. Для уравнения, полученного из кинематических соображений это допустимо. При этом надо заметить, что наблюдаемая энергия ведёт себя как потенциальная, т. е. её можно формально связать с энергией потенциального инерционного поля (можно добавить потенциальный член в уравнение). На замкнутом пути работа этого поля будет равна нулю. Поэтому вечные двигатели на основе силы Кориолиса и центробежной силы не возможны.
Покажем, что для маятника Фуко в неинерциальной системе отсчёта, в гармоническом случае, выполняется векторное дифференциальное уравнение
a = -ω2·r - 2·[Ω×v] + Ω2·r (3).
Для этого рассмотрим относительное кинематическое движение маятника в частном случае, реализованное через вращение по уравнениям:
Траектория эллипса в инерциальной системе отсчёта
Rx = -a·sin(ω·t);
Ry = b·cos(ω·t). Этот вариант реализует начальные условия пуска маятника при t = 0:
R0x = 0; R0y = b (пуск с отклонением от центра координат по малой оси); V0x = -a·ω; v0x = -a·ω + b·Ω.
...
Продолжение
Оглавление

|
|

