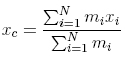|
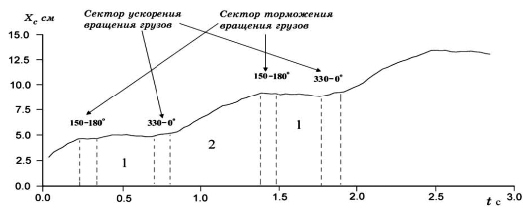
Экспериментальный график движения центра масс «Какие бы теоретические модели явления мы не строили, последнее слово, как всегда, за экспериментом. На рис. 4 представлен типичный экспериментальный график движения центра масс однотактного инерцоида, изображенного на рис. 1.
Рис. 4: Движения центра масс инерцоида Данные, представленные на рис. 4 были получены с использованием следующей методики. На горизонтальной гладкой поверхности стола была прикреплена линейка с ценой деления 1 мм. Сверху на специальной рельсе, параллельной столу, укреплена кинокамера, производившая съемку движения инерцоида. Эксперименты по киносъемке движения инерцоида Толчина были проведены в 1983 г. А. П. Гладченко. Инерцоид был изготовлен по чертежам, опубликованным в книге [1]. После обработки кинопленки с нее снимались следующие динамические переменные: а) координаты x1(t) грузов 5; б) координата тележки x(t). По этим данным с помощью формулы
вычислялась координата центра масс xc. Из графика видно, что в тех угловых секторах, в которых мотор-тормоз не действовал (не работала пружина 9), инерцоид двигался как свободный симметричный вибратор, т.е. его центр масс покоился или двигался с постоянной скоростью. Изменения скорости центра масс наблюдалось тогда, когда включался в работу мотор-тормоз (работает пружина 9). Дальнейшие исследования показали, что характер движения центра масс определяется не столько силой трения колес с подстилающей поверхностью, сколько формой кулачка 8 (угловыми секторами ускорения и торможения вращения грузов 5) и жесткостью пружины 9. График 4 получен для инерцоида, который стартует из состояния покоя (временной сектор 1 на графике). Движение корпуса инерцоида и его центра масс начинается в момент, когда мотор-тормоз ускоряет вращение грузов 5, что длиться примерно 1/10 сек (весь период примерно 7/10 сек). После окончания действия мотор-тормоза центр масс начинает двигаться с (почти) постоянной скоростью 5.7 см/сек до тех пор, пока не начнет опять работать мотор-тормоз (временной сектор 2 на графике). Теперь мотор-тормоз начинает уменьшать угловую скорость вращения грузов 5, в результате чего скорость центра масс падает до нуля. Этот процесс продолжается периодически до тех пор, пока завод пружины 6 поддерживает вращение малых грузов 5.
Рис. 2: Схематическое изображение однотактного инерцоида » (По данным опубликованым Г. И. Шиповым в 4D ГИРОСКОП В МЕХАНИКЕ ДЕКАРТА .) Из графика видно, что фазы активного перемещения виброхода по Гулиа и инерцоида по Толчину противоположны. Уже это одно должно серьёзно обратить на себя внимание официальной науки, однако этого не произошло. Движение инерцоида в моей теории соответствует варианту Толчина.
«Накрытый кожухом инерцоид движется точно так же, как и без него: корпус инерцоида продвигается относительно поверхности на 90 мм вперед и отступает на 30 мм Величины 90 мм и 30 мм можно вычислить.
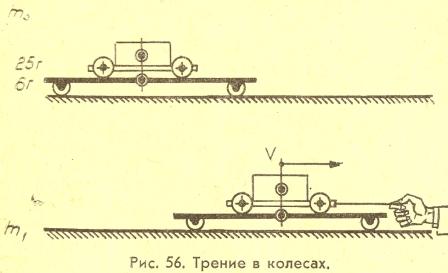
ПОВЕДЕНИЕ ИНЕРЦОИДА НА ТЕЛЕЖКЕ-ИНДИКАТОРЕ «На дорожку установить тележку-индикатор, а на нее — заведенный инерцоид и запустить его. Инерцоид пробегает по тележке-индикатору характерным для себя способом и сбегает с нее. Тележка-индикатор остается неподвижной. Тележка-индикатор еще раз объективно фиксирует отсутствие какой-либо продольной реакции в горизонтальном направлении. Это свидетельствует о том, что инерцоид не отталкивает тележку-индикатор и не отталкивается от нее сам при своем перемещении по ней. Окружающая воздушная среда тоже не может стать односторонней точкой опоры для инерцоида ввиду исчезающе малого сопротивления. Можно предположить, что инерцоид не отталкивает тележку-индикатор назад при своем движении вперед потому, что «сила трения» в колесах между тележкой-индикатором и дорожкой настолько велика, что тележка оказывается как бы приколоченной трением к дорожке [16]. Инерцоид не может сдвинуть ее с места своею силой. (Естественно, что усилие инерцоида, его тяга не может быть больше трения в его колесах. Иначе он проскользнет.) Такое предположение отпадает, если считаться с реальной картиной эксперимента. Величина трения из неподвижного состояния между колесами инерцоида и плоскостью тележки-индикатора составляет 25 г (рис. 56), а трение между колесами тележки-индикатора, нагруженной инерцоидом, и плоскостью дорожки; всего 6 г,
Если инерцоид, свободно поставленный на тележку-индикатор, потянуть осторожно за нитку, катится по дорожке тележка-индикатор, а инерцоид остается на ней неподвижным. После запуска инерцоида трение неподвижности в его колесах сменяется трением движения, которое значительно меньше 6 г. Поэтому теперь тележка-индикатор остается неподвижной, когда инерцоид перемещается по ней. При каждом такте инерцоид сначала перемещается вперед, а потом — назад. Однако такая смена направления движения не сопровождается возникновением трения неподвижности в его колесах. Чтобы трение неподвижности утвердилось, необходима достаточно длительная остановка, которой у инерцоида при смене направления перемещения не возникает. Поэтому он не тянет за собою тележку-индикатор как при перемещении вперед, так и при перемещении назад. Это говорит о том, что «нелинейность сил трения», если бы таковая существовала в колесах инерцоида, не должна была бы выходить за пределы совершенно ничтожной, даже по сравнению с 6 г, величины». ст. 49. Толчин, «Инерцоид»
Как отмечает Л. Б. Левенсон [4]: «С увеличением мощности и быстроходности участились поломки машин. Стало особенно заметно давнее разногласие по существенному вопросу о силах инерции: на первых двух курсах студентов учили в теоретической механике, что силы инерции вовсе не существуют, что они лишь воображаемые и вводятся в расчёт для удобства его, отнюдь не будучи реальными, что силы инерции условный геометрический вектор, математическая фикция и т.д. А через год в курсе тепловых двигателей их заставляли складывать действительные давления пара на поршень с несуществующей силой инерции движущихся частей, чтобы получить истинную результирующую силу. Всякое пренебрежение, всякий недоучет этой "вовсе не существующей" силы неизбежно влечет за собой поломки, крушения и тому подобные реальные последствия.» (По данным опубликованым Г. И. Шиповым в 4D ГИРОСКОП В МЕХАНИКЕ ДЕКАРТА .)
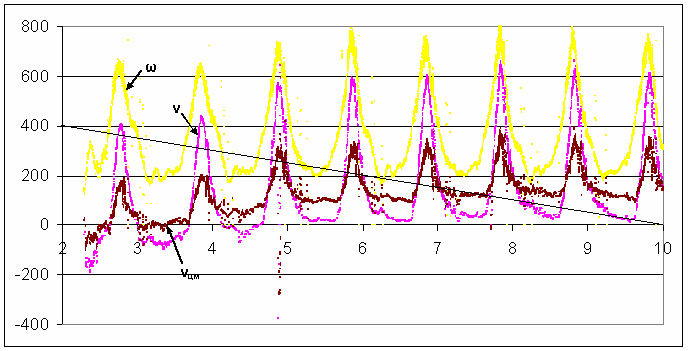
Противоречия движения инерциоида механике Ньютона. «Итак, давайте вернёмся к графикам движения инерциоида, из которых видно, что центр масс (ц.м.) периодически меняет свою скорость (Рис. 9). Ускорение, которое имеет ц. м. системы, составляет в некоторые интервалы времени величину порядка 1000 мм/сек2, что примерно в 20 раз превышает возможные ускорения под действием сил трения, и в 100 раз превышают ускорения от возможного наклона опоры. К тому же, поскольку в этой серии на показанном интервале инерциоид около 5 секунд движется без отката назад, силы трения могут быть направлены только против хода движения, и могут только препятствовать движению (на рисунке наклонной линией показано «нормальное» замедление инерциоида под действием установленных сил трения). И, даже если предположить, что в начальный период, когда инерциоид ходил вперёд и назад, имела место зависимость силы трения от направления либо скорости, то, «разогнавшись» таким образом, он мог затем только тормозиться. Но этого не происходит, более того, средняя скорость центра масс растёт при движении в одном направлении. Таким образом, силами трения такое движение ц. м. совершенно не объясняется.
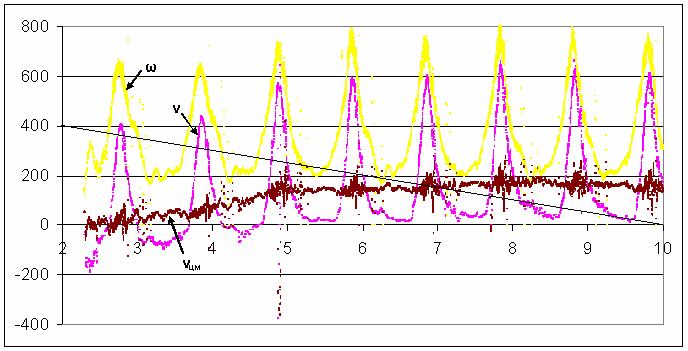
Рис. 9. Графики скоростей инерциоида. Наклонная линия – изменение скорости, которое должно быть под действием сил трения. Наконец, существует последняя возможность попытаться объяснить этот и аналогичные графики, не выходя из рамок механики Ньютона (и, разумеется, в предположении, что инерциоид не дёргают периодически резко за шлейф и не толкают руками). Что, если имеется ошибка при расчёте скорости ц. м.? Формула для расчёта скорости ц.м.: Vцм = V – B ω sin(φ) Значение параметра B задаётся в файлах данных для каждой серии. В приведённом графике параметр B равен 0.022 м (что соответствует массе груза 170 г). Попробуем так подобрать этот параметр, чтобы убрать пики скорости ц. м. На Рис. 10 показана та же серия, но при подобранном параметре B = 0.034 м (тогда масса одного груза составляла бы 310 г). Хотя пики первого порядка ушли, но всё равно остаётся непонятным поведение тренда скорости ц.м.: что-то разгоняет инерциоид против сил трения и не даёт ему остановиться. К тому же маловероятна ошибка учёта массы грузов в 2 раза.
Рис. 10. График скоростей при параметре B = 0.034 м. » Эта кажущаяся ошибка учёта массы, предсказывается в моём варианте теории инерцоида. Она точно равна двум. Теория также объясняет, почему скорость центра масс значительно выше уровня, который должен быть, если считать трение основным движущим фактором. Движение описанное в этом опыте соответствует численной модели инерцоида Страница_5.
ОДНОТАКТНЫЙ ИНЕРЦОИД НА НАКЛОННОЙ ПЛОСКОСТИ «Однотактный инерцоид без детектирования обратного импульса в переднем направлении при очень малом трении в колесах не может преодолевать сколько-нибудь существенного встречного уклона дорожки. В этом случае к инерцоиду предъявляются очень жесткие требования. Трение в его колесах должно быть минимальным, чтобы не загрязнять инерцоидный процесс. Это требование выполняется. Малое трение увеличивает чувствительность инерцоида к встречным уклонам дороги. При малом трении инерцоид может успевать скатываться назад, пока не работает передний импульс, тем более что задний импульс помогает этому нежелательному скатыванию. Опытом установлено: если встречный уклон меньше критического, то инерцоид преодолевает его и поднимается в гору. Если встречный уклон равен критическому, инерцоид колеблется около одного постоянного положения. Если встречный уклон немного больше критического, инерцоид постепенно скатывается с него, задерживаясь при каждом такте, когда работает передний импульс. Учитывая данные опытов, нельзя сказать, что инерцоид совсем не может преодолевать встречных уклонов. Если этот уклон не больше критического, механизм преодолевает его. У инерцоида с пружинным заводом критический уклон немного больше пяти минут. У более тяжелых однотактных инерцоидов критический уклон колеблется около одного — полутора градусов. Если встречный уклон дороги значительно больше критического, происходит детектирование переднего импульса в заднем направлении. Инерцоид начинает скатываться с прогрессирующим ускорением. Ни от одной известной технике машины не требуют, чтобы при свободных колесах она не скатывалась под уклон, когда не работает вперед её двигатель. Такое требование было бы очевидно невыполнимым. От однотактного инерцоида некоторые специалисты непременно ожидают выполнения этого противоестественного условия. Если встречный уклон по своей длине меньше, чем ход инерцоида за один такт, то инерцоид преодолевает значительные встречные сопротивления, уклоны и даже ступеньки лестницы. Крохотный однотактный инерцоид с, пружинным заводом свободно преодолевает ступеньки высотою 4 мм при диаметре своих колес 40 мм и даже с нагрузкой 250 г (рис. 60)» «Инерцоид» ст. 62. Толчин своими исследованиями на наклонной плоскости показал, что инерцоид это прецизионный механизм и требует для выявления его действительных свойств особые условия. Инерцоид на неровном столе демонстрирует на большой процент обыкновенный виброход (кузнечик Гулиа) и соответственно ни чего не доказывает и только морочит всем голову. Это конечно один из факторов, который превращает инерцоид в механический призрак. Именно на гладкой эквипотенциальной плоскости при ничтожном трении в колёсах, только тогда можно, что-либо утверждать. Толчин это прекрасно понимал и стремился уменьшить трение как мог. |
||

Механика инерцоида
| ||
| Главная | Опыт | Мой профиль | Выход | Вы вошли как Гость | Группа " Гости" | RSS |  |