Выше

...

      В следующей серии экспериментов менялись положения секторов ускорения и торможения. Положение сектора ускорения оказалось близко к оптимальному. Оптимальное значение начала сектора торможения φ₁ оказалось близко к 90° (φ₁ ≈ 89.5 ± 0.5°). При этом значении φ₁

Инерцоиды В. Н. Толчина не нуждались в такой оптимизации. Он устанавливал зоны ускорения и торможения, исходя из наименьшего их влияния на процесс движения инерцоида. «Действие двигателя не сказывается на поведении корпуса механизма, если включение двигателя производится не раньше минус 330 градусов». ст. 10. «Инерцоид». Поэтому этот способ увеличения скорости виброхода не имеет отношения к инерцоидам В. Н. Толчина.

v ≈ 4.27 см/с; в случае значения φ₁ = 160°, использованного В. Н. Толчиным, значение средней скорости v ≈ 2.01 см/с. С учётом этого обстоятельства дальнейшие расчёты (первый вариант) велись при

φ₁ = 160°,       γ = 0.3,      r = 0.3,      c₂ = 20,      c₃ = 19     

(4.15)

и различных значениях величины трения c₁.

      На рис. 5 сплошной линией представлена зависимость средней скорости установившегося движения инерцоида v от величины трения. Как видно, обычно уменьшение трения приводит к увеличению скорости. Однако, существует небольшой интервал c₁ = 0.4 ÷ 1.1, в котором скорость уменьшается при уменьшении трения.

      Интервал c₁ = 0.4 ÷ 1.1, соответствует интервалу μ_ос1 = 0.816 ÷ 2.243 (μ_ос1= k₁·c₁/g). Величина нижней границы этого интервала больше, чем у колеса инерцоида, изготовленного из мелкозернистого шлифовального камня с осью из чугуна, работающего без смазки (μ = 0.72 в движении, для оси из железа и стали μ = 1.0). Очень трудно представить себе, что Толчин мог применять подобные колёса. Верхний предел интервала, даёт трение больше веса инерцоида и поэтому совсем не реален. Практика сильно завышать трение, очень характерна для оппонентов В. Н. Толчина, так как при маленьком трении не удаётся получить расчётное ускорение соответствующее опыту. Однако даже при сильном завышении трения, скорость программной модели центробежного виброхода всегда меньше скорости эквивалентного инерцоида при той же тактовой частоте.
      Если сделать пересчёт нижней границы интервала на абсолютное трение, в применении к "пружинному" инерцоиду, то получим 0.4·950/9.80665 = 38.75 грамм. Для этого случая у В. Н. Толчина в книге «Инерцоид» есть следующий комментарий.
«Трение в колёсах инерцоида можно увеличить до 60 г (c₁ = 0.62), если затормозить одну пару колёс дополнительной тележки инерцоида. При этом условии инерцоид проходит расстояние 500 мм за 9–10 с (без тормоза за 2–2.5 с). Причём, после завершения каждого такта назад не отходит, продвигаясь в каждом такте только вперёд», ст. 57.
Из рис. 5 видно, что точке c₁ = 0.62, можно найти точку c_1а < 0.4 в которой скорость виброхода будет равной. За пределами точки c_1а, при уменьшении трения, скорость виброхода фактически может возрастать в 4 ÷ 4.5 раза. Это значит, что "пружинный" инерцоид работает при c₁ < 0.4 (сама точка c₁ = 0.4 не подходит по фрикционным свойствам).
При трении покоя 25 грамм – c₁ = 0.26. На ст. 201 Автор статьи считает, что именно увеличение трения с 25 грамм до 60 грамм, понижает скорость инерцоида в 4 ÷ 4.5 раза, т. е. точка c₁ = 0.26 является рабочей для "пружинного" инерцоида. Однако это противоречит опытам на индикаторной тележке с трением покоя в 6 грамм. Инерцоид в движение не может нарушить её покой. Поэтому В. Н. Толчин и утверждает, что сила трения в движении < 6 грамм это соответствует c₁ < 0.062. Программный виброход при трении в 6 грамм не соответствует параметрам инерцоида при равной тактовой частоте. Форма траектории грузов слишком округлёна. Динамика центра масс не соответствует реальному опыту. Скорость значительно меньше. ...
      На рис. 5 пунктирной линией показана зависимость скорости в случае
f₁(v) = -c₁·sign(v) - c₄·v|v|, при c₄ = 0.4. Член -c₄·v|v|, описывает сопротивление при движении в жидкости. Эта составляющая трения всегда уменьшает скорость движения виброхода вперёд. Эту зависимость можно использовать и для аппроксимации сухого трения в зоне его спада от уровня трения покоя, при c₄ < 0. ...

Локальный максимум v ≈ 5.27 см/с соответствует c₁ ≈ 1.08; локальный минимум v ≈ 3.25 см/с достигается при c₁ ≈ 0.04?. При малых значениях трения (c₁ < 0.1) первая модель не даёт установившегося решения – за каждый такт увеличивается скорость вращения грузиков. Это обстоятельство явно говорит о неадекватности первой модели с реальным устройством. В этой модели в каждом периоде имеется добавка к энергии вращательного движения, равная

ΔE = γ·R²·(c₂·(φ₄ - φ₃) - c₃·(φ₂ - φ₁)).

(4.16)

      Если затраты на трение меньше, чем ΔE, угловая скорость вращения грузиков будет неизбежно нарастать. Из дифференциального уравнения видно (вычислительный эксперимент подтверждает это), что при малом внешнем трении dω/dφ ∼ 1/ω.

c₁ = 0.1 это μ₁ = 0.01 или μ_ос1 = 0.195 (μ_ос1= 3·k₁·c₁/g/π). Это значение параметра уже близко к диапазону трения, в котором работают инерцоиды, но факт неадекватности модели не позволяет нам исследовать поведение виброхода при c₁ < 0.1, в переделах этой модели, а жаль.

      Этих недостатков лишена вторая модель, в ней независимо от внешнего трения всегда возможен периодический режим вращения. Но прежде чем перейти к результатам испытания второй модели, опишем ещё результаты расчёта по первой модели с добавлением к внешнему кулоновскому сопротивлению квадратичного слагаемого

f₁(v) = -c₁·sign(v) - c₄·v|v|.

(4.17)

      При c₄ ≠ 0 первая модель позволяет достичь установившегося режима при c₁ → 0. Пунктирная линия на рис. 5 соответствует расчётам при c₄ = 0.4. Как видно, эта квадратичная добавка к трению существенно сказывается при c₁ < 0.4.

После локального максимума v_с ≈ 4.16 при c₁ ≈ 0.25 средняя скорость падает с уменьшением c₁ и достигает нуля при c^,₁ ≈ 0.135. При c₁ < c^,₁ инерцоид в среднем движется в обратную сторону (v < 0), достигая при c₁ = 0 значения v ≈ - 1.22 см/с. Этот факт не удивителен. При c₁ = 0 работает только квадратичное слагаемое в (4.17). Расчёты [9] с таким трением всегда давали движение инерцоида с v < 0.
    Перейдём к описанию результатов расчёта по второй модели с тормозящим моментом (4.7). Для предварительного выбора параметров c₂, c₃ можно использовать точные решения динамики вращения в предположении неподвижности корпуса инерцоида (v = 0). В этом случае изменение угловой скорости происходит только в секторах ускорения и торможения. Пусть после торможения угловая скорость ω = ω₀, а после ускорения ω = ω₁. Для определения ω(t) необходимо решить две задачи Коши: ...

    Перейдём к обсуждению результатов расчёта при

γ = 0.3,    R = 0.3,     c₂ = 65,      c₃ = 10,      c₄ = 0

(4.25)

Здесь надо обратить внимание на особенности тормозного устройства, реализованного по закону , так как , то можно записать равенство
. Это дифференциальное уравнение можно проинтегрировать



. Изменение угловой скорости однозначно определяется выбранными параметрами и углом торможения. Однако, для нас важнее посмотреть на решение этого дифференциального уравнения, которое можно записать так

Интеграл на интервале времени от этого выражения равен



   При t → ∞

, т. е. существует пороговое значение , которое грузы уже не могут преодолеть. Так как в этой формуле параметры , , заданы, то момент инерции грузов, т. е. фактически масса виброхода, не может быть меньше величины приблизительно равной
.   При 20°, 11.5 рад/с, 10, r = 0.3 м, γ = 0.3
 11.24 кг. Это факт не имеет значения с точки зрения оценки влияния трения на движение виброхода, однако физически такая зависимость массы виброхода от параметров и не корректна. При величине массы виброхода меньше этого значения он не сможет преодолеть вязкое сопротивление тормозного механизма. Это подтверждается численным моделированием этой ситуации. Для поддержания определённой разности частот между полутактами потребуется ещё большая масса 36.94 кг, при
 11.5 - 8.0 = 3.5 рад/c. При уменьшении массы виброхода при той же разности частот необходимо пропорционально уменьшать коэффициент . ...

и различных c₁ (положение секторов ускорения и торможения соответствовало (1.1)). Для указанных параметров из формул (4.21, 4.22) следует, что ω₀ ≈ 8.00, ω₁ ≈ 11.50, T ≈ 0.660 (по формуле (4.24) период примерно 1% меньше). Расчёты показали, что действительно при больших значениях трения, когда инерцоид в основном стоит, период согласуется с формулой (4.22). При малых значениях c₁ период немного меньше. Так, например, при c₁ = 0.10 T ≈ 0.637 с. При средних значениях c₁ близких к c₁ ≈ 2.0 период достигает максимального значения T  ≈ 1.12 с.
    Обсудим периодические зависимости x(φ), v(φ), ω(φ), изображенные на рис. 6. Характер движения x(φ) согласуется с представленными данными изобретателя инерцоидов [3].

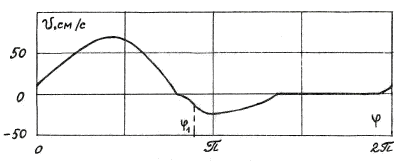
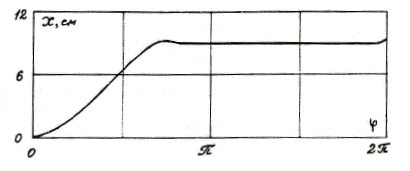
Согласно [3] каждый такт инерцоида начинается с покоя. Это не совсем так, и наиболее отчётливо это видно на зависимости скорости от угла v(φ), – интервал с нулевой скоростью заканчивается в конце периода при φ ≈ 343°. Максимум x (ход вперёд), равный 5.94 см, соответствует φ ≈ 144°. После этого инерцоид движется в обратную сторону (ход назад), затем покоится в интервале φ от 246° до 343°. Максимум скорости v ≈ 68.9 см/с достигается

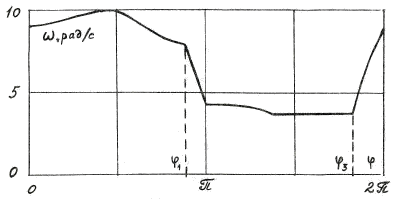
   Рис. 6    Зависимости x(φ), v(φ), ω(φ) в установившемся периодическом режиме для параметров (4.25) при c₁ = 2, φ₁ = 160° (вторая модель)

c₁ = 2 это μ_ос1 = 3·k₁·c₁/g/π = 3·20·2/9.80665/π = 3.895. Поэтому графикам, приведённым на рис. 6 и 7 невозможно поставить в соответствие подобное движение реального инерцоида В. Н. Толчина. Эти графики демонстрируют формальное движение виброхода при уровне трения значительно выше того, которое можно получить при использовании стандартных материалов для изготовления колёс. ...

при φ ≈ 78°, затем скорость уменьшается до нуля при φ ≈ 144° (этот момент соответствует максимуму x) и достигает наименьшего значения v ≈ -24.4 см/с при φ ≈ 179°. И, как уже отмечалось при обсуждении зависимости x(φ), в интервале φ от 246° до 343° скорость равна нулю. Увеличение трения, естественно, увеличивает этот интервал. В зависимости угловой скорости от угла отчётливо видны изменения ω на интервале торможения (160° – 180°) и ускорения (330° – 360°). Максимум угловой скорости ω ≈ 9.98 рад/с достигается при угле φ ≈ 79°; на интервале без движения (v = 0) угловая скорость имеет минимальное постоянное значение ω ≈ 3.74 рад/с. Выход на обсуждаемый установившийся режим движения осуществляется за 7 периодов (v(0) = 0, ω(0) = 6.9) с точностью до (см.(4.12)) ε = 10^-3. При этом величина de (4.11), характеризующая степень выполнимости закона сохранения энергии, убывает по модулю от значения на первом шаге, примерно равном -36.5% с множителем ≈ 0.19 – 0.25.
    На рис. 7 показаны зависимости x(φ), v(φ), ω(φ) для параметров, которые соответствуют таковым на рис. 6, но для оптимального положения сектора торможения с началом φ₁ = 114°. Интегральные характеристики обсуждаемых случаев таковы (см. табл. 2).

Таблица 2

    По рисункам и интегральным характеристикам видно, что при оптимальном варианте расположения сектора торможения значительно уменьшена возвратная фаза движения инерцоида. Именно это обстоятельство в основном и приводит к повышению средней скорости более чем в 2 раза.
    На рис. 8 представлена зависимость средней скорости инерцоида v_ср от величины c₁ для параметров (4.25) со значениями секторов ускорения и торможения согласно (1.1). Как видно, в широком интервале значений трения скорость монотонно убывает с ростом c₁. Отличия от монотонной зависимости наблюдаются для областей малых (c₁ < 0.3) и больших значений трения (c₁ > 11.3). Максимум v_ср ≈ 18.51 см/с достигается при c₁ ≈ 0.33; при c₁ → 0 v_ср →≈ 17.4 см/с.

Перемещение за период при c₁ → 0 примерно равно 17.4 см/с·0.637 с = 11.084 см., т. е. практически равно перемещение в оптимизированном варианте при c₁ = 2, 11.67·1.04 = 12.137 см. Увеличение скорости произошло только за счёт увеличения тактовой частоты. Это перемещение меньше амплитуды 18 см. Оно меньше амплитуды и при c₁ ≈ 0.33, т. е. в максимуме скорости. Подобная ситуация не соответствует реальному движению инерцоида. ...

Три стрелки на рис. 8 показывают увеличение v_ср при смене фиксированного значения начала

   Рис. 7    Зависимости x(φ), v(φ), ω(φ) в установившемся периодическом режиме для параметров (4.25) при c₁ = 2, φ₁ = 114° (вторая модель)

сектора торможения φ₁ = 160° на оптимальное φ°₁. Оптимальное значение начала сектора торможения оказалось зависящим от величины трения. Так, оптимальные значения φ°₁ для значений c₁ = 2, 3, 4 соответственно равны 114°, 105°, 136°, а соответствующие коэффициенты увеличения средней скорости ≈ 2.19, 1.77, 1.11. ...

   Результаты расчётов, представленные на рис. 5, 8, показывают сильную зависимость скорости инерцоида от величины трения. Причём, наряду с типичной и легко понимаемой убылью скорости при возрастании трения, существуют области с "аномальной" зависимостью; на границе указанных областей dv_ср/dc₁ = 0. Выполненные расчёты соответствуют двухпараметрической модели трения (4.17), в которой параметр c₄ обычно полагался равным нулю. Реальные зависимости силы трения от скорости сложнее. В частности, не учтена убыль трения при возникновении движения (область малых значений скорости). Согласно данным [3] трение качения в 3 – 4 раза меньше трения покоя. Учёт этого факта потребует добавления в (4.17) как минимум ещё одного параметра.
   Выполненные расчёты показывают, что вторая модель, в которой учтено трение при вращении грузиков, достаточно адекватно описывает типичные особенности движения инерцоидов. Кроме того, показано, что существуют богатые возможности для определения оптимальных параметров устройств подобного типа.

Библиографический список

    1.  Толчин В. Н. Основные начала механики в материалистическом понимании. Пермь, 1968. С.114.
    2. Толчин В. Н. Искусственная точка опоры и однотактный инерцоид/НТО СССР. 1969. № 12. С.22–24.
    3. Толчин В. Н. Инерцоид (силы инерции как источник поступательного движения). Пермь: Перм. кн. изд-во, 1977. 99 с.
    4. Деринг Г., Черных В. Инерцоид инженера Толчина//Урал. 1969. № 7 С.108–120.
    5. Деринг Г. Честь борьбы (документальная повесть)//Уральский следопыт. 1971. № 9 С.10–20; № 10. С.39–51.
    6. Черных В. Так существует ли инерцоид? (6 лет спустя)//Урал. 1976. № 10. С.140–149.
    7. Инерцоид инженера Толчина (отклики, комментарии)//Урал. 1970. № 5. С.113–110.
    8. Возможно ли движение без опоры? Эксперименты, которые надо объяснять. Силой волн – к звёздам // Тех. молодёжи.  1969. № 4. С.28–31;  № 6. С.16–19; 
Китайгородский А. Безумные идеи – глупые идеи // Там же. 1970. № 10. С.24–27;
Казакевич В. Под гипнозом предубеждённости // Там же. 1973. № 8. С.16–18; № 9. С.8–9;
Игра в "Инерцонику" // Там же. 1974. № 3. С.25–26;
Гулиа Н. В. Инерцоиды без инерции. Некролог по инерцоиду // Там же. 1979. № 3. С.17–19;
    9. Жуховицкий Е. М., Тарунин Е. Л., Шапошников И. Г. К теории инерцоида// Учён. зап. Перм. ун-та. 1972. № 257. С.89–98.
   10. Геронимус Я. А. Попытки ниспровергнуть законы классической механики//Теоретическая механика: Очерки об основных положениях. М.: Наука, 1973. С.487–490.
    11. Могильнер А. И. Интегрирование уравнений движения инерцоида. М.,1980. Деп. ВИНИТИ, № 3368–80.
    12. Гулиа Н. В. История одного заблуждения//Юный техник. 1981. № 1. С.63–65.
    13. Гулиа Н. В. Инерционные "химеры"//Инерция. М.,: Наука, 1982. С.144–150.
   14. Александров А. Кажущиеся очевидности и мнимые парадоксы (как распознать вечный двигатель) // Изобретатель и рационализатор. 1985. № 7. С.20–23.
    15. А.с. 1029219 СССР с приоритетом от 05.06.80. Прибор для демонстрации движения центра масс механической системы по инерции. Сметанников Е.С.(СССР)
    16. Физический энциклопедический словарь. М.: Сов.Энциклопедия, 1960. Т. 2.
    17. Шипов Г. И. Теория физического вакуума (новая парадигма). М., 1993. 362 с.
    18. Шипов Г. И. Об использовании вакуумных полей кручения для перемещения механических систем. М., 1991. 50 с.
    19. Бронштейн И. Н., Семендяев К. А. Справочник по высшей математике. М.: Изд-во техн.-теор.лит. 1955. 608 с.
    20. Грандштейн И. С., Рыжих И. М. Таблицы интегралов, сумм, рядов и произведений. М., 1963.
    21. Ахматов А. С. Молекулярная физика граничного трения. М., 1963. 472 с.
    22. Андронов А. А., Витт А. А., Хайкин С. Э. Теория колебания. М., 1959.
    23. Камышов В. Авто зовут инерцоид// Свет. 1993. № 12. С.12–14.
    24. Лебедев Н. Ф. Инерцоид В. Н. Толчина. Письмо редактору журнала "Свет" В. И. Захаренкову// Свет. 1994. № 4.