Выше

Михаил, желаю Вам самого Доброго Вечера!
      
1.    Михаил, Вы, как обычно, полностью игнорируете мои замечания, стараясь «любой ценой» высказать собственные мысли, являющиеся важными для Вас лично, но не являющиеся при этом ответами на мои. В связи с этим и мне ничего не остаётся, как вновь и вновь обратить Ваше внимание на то, что является важным для меня.

Владимир Максимович это не так. По возможности я пытаюсь ответить на Ваш вопрос, однако мой ответ часто уходит в неожиданном для Вас направлении и это от меня зависит только частично, всё определяется законами механики согласованными с опытом.

       Формула М = Т·R и в этом случае правильна.

2.    В этой формуле всего два сомножителя. Один из них – это постоянная величина R, не равная нулю. Другой – переменная величина Т, не равная нулю, хотя бы в обсуждаемой позиции.
У меня Т = m·(g·cos(α) - R·dω/dt). При g·cos(α) = R·dω/dt, будет Т = 0. Вы фактически считаете, что Т = m·g·cos(α) и это неправильно.

       Я пока оставляю без внимания Вашу традиционную попытку перейти от обсуждения Фомы к обсуждению Ерёмы и посему не спорю о том, что в соответствии с теорией относительности вес тела изменяется в зависимости от скорости его перемещения. В нашем конкретном случае мгновенный вес груза считается постоянным. Следовательно, постоянной по величине является и мгновенная компонента Т.
Теория относительности здесь не причём. Вес тела и масса тела это разные понятия. Вес тела зависит от ускорения опоры, на которой оно находится, т. е. P = m·(g - a_y) и в условиях ускоренного движения не является постоянным. Вес это сила, с которой тело давит на опору и эта сила определяет динамику взаимодействия с опорой, т. е. с направляющей в нашем случае.

       Но тогда получается, что произведение постоянной величины R, не равной нулю, на постоянную величину Т, не равную нулю, просто обязано выдать на выходе некий результат, не равный нулю!
Ноль может быть при g·cos(α) = R·dω/dt. Это уравнение движения математического маятника.

       В нашем случае этот результат – ни что иное как, момент вращения, формируемый на роторе падающим грузом. Причём, повторяюсь, это произведение (а значит, и момент вращения) НЕ РАВНО НУЛЮ!
       Здравый смысл не может согласиться с этой логикой. Ему понятно, что на роторе соосно с его собственной осью можно жёстко закрепить деталь, которую в дальнейшем удобнее называть «подвеской». На эту подвеску свободно навешивается тяга, имеющая возможность свободного вращения вокруг оси подвески, а значит, и вокруг оси ротора. Ему (здравому смыслу) понятно, также, что никакое вращение свободно навешанной тяги вокруг оси подвески не сможет привести ротор во вращение, если считать трение качения пренебрежимо малым. «Здравый смысл» очень коварный товарищ и часто вводит в заблуждение.

3.    Вывод – предельно прост. Предложенная Вами методика некорректна!
Только в Ваших неверных предположениях. Моя методика выводит на общеизвестные уравнения движения математического маятника, что соответствует рассматриваемой задаче и косвенно указывает, что мой метод верен.

4.    Я предлагаю другой подход.

       -    Если груз может перемещаться только по строго заданной траектории, то единственная сила, которая может передаваться ротору и воздействовать на него, это мгновенная компонента Т от вектора Р (вес груза), касательная к траектории в мгновенной точке контакта её с грузом.
Это так.
       -    Сила может передаваться ротору только по линии, соединяющей центр масс груза с осью подвески. Такую силу можно отобразить совпадающим с обозначенной линией вектором Q, взятой от вектора Т.
Нет, это не так. Силы, связанные с моментом, передаются касательными силовыми факторами, т. е. за счёт изгиба подвески груза, а не за счёт растяжения или сжатия. И далее, тоже будет неверно.

       -    Искомый момент равен произведению расстояния от оси вращения ротора на модуль вектора Q.
       -    В этом случае, при совпадении оси подвески с осью ротора, расстояние от оси ротора до вектора Q автоматически обнуляется. А вместе с этим обнуляется и момент вращения.

Обратите особое внимание!

Вес тела зависит от ускорения опоры, т. е. P = m·(g - a_y) и это закон проверен опытом. Его игнорирование, приводит к заведомо неверным результатам, что и наблюдается в Вашем варианте решения задачи. Невесомость есть P = m·(g - a_y) = 0, т. е. g = a_y, тело свободно падает. В теории относительности масса (не вес) тела зависит от скорости (не от ускорения).

Момент всегда передается на ось касательными силовыми факторами, т. е. через изгиб, что является тоже законом проверенным опытом. Момент не относится к центральным силам (действующим по прямой на ось), он всегда перпендикулярен им. Игнорирование этого факта приводит к неверным выводам.

Момент равен М = m·(g·cos(α) - R·dω/dt)·R. Он зависит от углового ускорения ролика dω/dt и от углового положения ролика α и это соответствует опыту. При g·cos(α) = R·dω/dt момент равен нулю и происходят свободные колебания маятника на оси. Это и есть случай движения, который мы рассматриваем. Если dω/dt = 0, это статический вариант, тогда М = m·g·cos(α)·R. В этом случае P = m·g и подвеска груза нагружена моментом, но в общем случае всегда
P = m·(g - a_y). ...

С уважением, Михаил. Жду вопросов.

16.10.2011 г.

В уравнении Т = m·(g·cos(α) - R·dω/dt):
g     –  ускорение свободного падения;
α     –  угловая ориентация линии, соединяющей центр груза с осью ротора;
ω    –  угловая скорость груза;
t     –  время протекания процесса;
dω/dt – угловое ускорение груза, т. е. производная от угловой скорости по времени;
m   – масса груза;
R    – расстояние от оси до груза.

Я предполагаю, что угловая  скорость ротора появляется от факта падения груза. Я могу предположить также, что в самое первое мгновение начала такого падения мгновенная угловая скорость ротора равна нулю по определению, а приращение угла поворота ротора от ускорения свободного падения груза слишком мало, чтобы серьёзно повлиять на величину компоненты Т.
       Другими словами, в первое мгновение начала падения груза в обсуждаемой позиции мгновенная величина вектора Т уж точно НЕ равна нулю.
В частном случае (начальную угловую скорость мы всегда можем задать по условию задачи), в первое мгновение движения можно считать, что ω = 0.
Если ось ротора ненагружена, то М = 0 и соответственно М = Т·R = 0, т. е. Т = 0. Момент всегда определяется внешними силовыми факторами, т. е. нагрузкой на оси. Если нет нагрузки, нет момента.

Т = m·(g·cos(α) - R·dω/dt).

Из этого уравнения мы можем выразить угловое ускорение, однако удобнее это сделать из уравнения для момента, который приложен к оси ротора или к подвеске груза
М = Т·R = m·(g·cos(α) - R·dω/dt)·R;

М/(m·R²) = (g/R)·cos(α) - dω/dt;

dω/dt = g·cos(α)/R - М/I, где I = m·R² – момент инерции груза. Это уравнение позволяет определить угловое ускорение при любом α и заданном моменте М.

Информация к размышлению для продолжения темы.

По правилам дифференцирования dω/dt = (dω/dα)·(dα/dt) = ω·(dω/dα), так как ω = dα/dt, тогда

ω·(dω/dα) = (g/R)·cos(α) - М/I, в этом уравнении возможно разделение переменных

ω·dω = (g/R)·cos(α)·dα - (М/I)·dα, интегрируем это уравнение

∫ ω·dω = (g/R)·∫cos(α)·dα - (М/I)·∫dα, при М = const (для упрощения задачи).

(ω₁² - ω₀²)/2 = (g/R)·(sin(α₁) - sin(α₀)) - (М/I)·(α₁ - α₀);

ω₁² - ω₀² = 2·(g/R)·(sin(α₁) - sin(α₀)) - 2·(М/I)·(α₁ - α₀), где α₀ – начальный угол; α₁ – конечный угол движения; ω₀ – начальная угловая скорость; ω₁ – конечная угловая скорость.

Помножим на момент инерции груза
I·ω₁²/2 - I·ω₀²/2 = (g·m·R)·(sin(α₁) - sin(α₀)) - М·(α₁ - α₀), где будет I·ω²/2 – кинетическая энергия груза; М·(α₁ - α₀) – работа момента силы по перемещению груза; R·(sin(α₁) - sin(α₀)) – фактически высота падения груза, тогда

ΔE = I·ω₁²/2 - I·ω₀²/2 = g·m·Δh - М·(α₁ - α₀) – изменение кинетической энергии тела при падении пропорционально высоте, моменту и угловому перемещению.

...

17.10.2011 г.

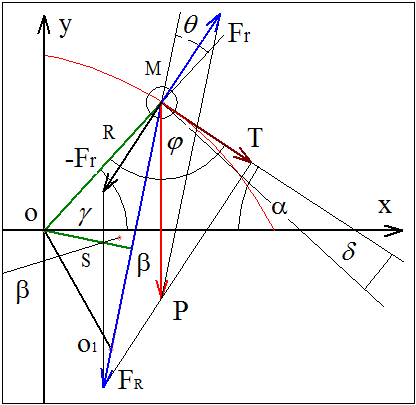
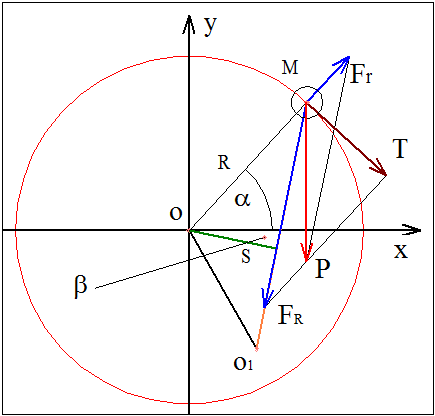
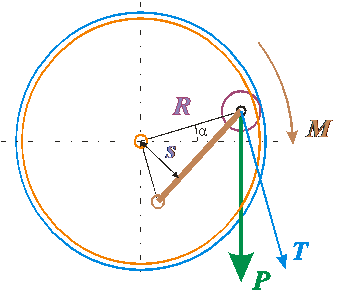
       При переходе к более общему случаю, когда направляющая уже не является окружностью угол между R и T не равен 90°. Поэтому формула для момента с учётом этого факта будет другая.

Формула для силы T запишется так
T = P·sin(α).

Рычаг силы F_R равен
S = R·cos(β + γ).

Сила T через силу F_R равна
Т = F_R·cos(φ - (90° - γ - β)) = F_R·cos(-90° + γ + β + φ) =

= F_R·cos(270° + γ + β + φ) = F_R·sin(γ + β + φ).

Момент на роторе равен
М = F_R·S = Т/sin(β + γ + φ)·R·cos(β + γ) = Т·R·cos(β + γ)/cos(β + γ - δ), где δ = 90° - φ.

М = P·R·sin(α)·cos(β + γ)/cos(β + γ - δ). Переход к некруговой направляющей существенно усложняет формулу для момента, так не позволяет сократить косинусы из-за δ, где δ – угол отклонения от окружной направляющей. Обратите внимание, что расчётная модель основанная на прямом применении силы Т из которой следует, что М = Т·R·sin(φ) = Т·R·cos(δ), в этом случае даёт уже неправильный результат, что не сразу очевидно. В этом случае происходит потеря составляющей момента обусловленной взаимодействием ролика с направляющей (F_r уже не со направлена с радиусом и поэтому тоже даёт момент).
Так как от углов β и γ зависит состояние механизма, то при наличии ненулевого δ появляется зависимость момента от положения тяги и груза. Степень этой зависимости определяется угловой величиной отклонения направляющей от окружности.

Пусть θ = 90° - β - γ, где θ – угол между радиусом и тягой. Тогда момент можно записать так

М = Т·R·cos(β + γ)/cos(β + γ - δ) = Т·R·cos(90° - θ)/cos(90° - (θ + δ));

М = Т·R·sin(θ)/sin(θ + δ).

При θ + δ = 0 существует особая точка, в которой момент стремится к бесконечности. Покажем, что в этом случае угол между тягой и касательной к направляющей составляет 90°.

Надо доказать, что β + 90° - α = 90°, т. е. β - α = 0; β = α.

При условии, что θ + δ = 90° - β - γ + 90° - φ = 0;

180° - β - γ - φ = 0 или 180° - α - γ - φ = 0; α + γ + φ = 180°, что и требовалось доказать.

В этой особой точке груз скользит по направляющей без давления на неё. В этом случае движение груза, при отсутствии трения, не зависит от приложенного к ротору момента, а определяется только весом груза.

Запишем формулу момента через сумму

М = Т·R·cos(β + γ)/cos(β + γ - δ) = Т·R·cos(β + γ - δ + δ)/cos(β + γ - δ) =

= Т·R·(cos(β + γ - δ)·cos(δ) - sin(β + γ - δ)·sin(δ))/cos(β + γ - δ) =

= Т·R·(cos(δ) - tg(β + γ - δ)·sin(δ)) = Т·R·(cos(90° - φ) - tg(β + γ - (90° - φ))·sin(90° - φ)) =

= Т·R·(sin(φ) - tg(β + γ - 90° + φ))·cos(φ)) = Т·R·(sin(φ) - tg(270° + β + γ + φ))·cos(φ)) =

= Т·R·(sin(φ) + ctg(β + γ + φ))·cos(φ)) =

Так как α + γ + φ = 180° имеем γ + φ = 180° - α.

М = Т·R·(sin(φ) + ctg(β + 180° - α)·cos(φ)) = Т·R·(sin(φ) + ctg(β + 180° - α)·cos(φ)) =

= Т·R·(sin(φ) - ctg(α - β)·cos(φ)).

По теореме синусов имеем
F_R/sin(180° - α) = F_r/sin(β) = P/sin(180° - β - (180° - α)).

F_R/sin(α) = F_r/sin(β) = P/sin(α - β).

Из рисунка имеем
(F_r + P·cos(α))/Т = ctg(α - β).

М = Т·R·(sin(φ) - (F_r + P·cos(α))/Т·cos(φ)) =

= Т·R·sin(φ) - R·(F_r + P·cos(α))·cos(φ)) =

= Т·R·sin(φ) - F_r·R·cos(φ) - P·R·cos(α)·cos(φ) =

= Т·R·sin(180° - α - γ) - F_r·R·cos(180° - α - γ) - P·R·cos(α)·cos(180° - α - γ).

М = Т·R·sin(α + γ) + F_r·R·cos(α + γ) + P·R·cos(α)·cos(α + γ).

М = Т·R·sin(α + γ) + P·R·sin(β)·cos(α + γ)/sin(α - β) + P·R·cos(α)·cos(α + γ).

Проверки при характерных углах:

Для окружной направляющей α = 90°- γ.

М = Т·R·sin(90°- γ + γ) + F_r·R·cos(90°- γ + γ) + P·R·cos(90°- γ)·cos(90°- γ + γ) = .

= Т·R·sin(90°) + F_r·R·cos(90°) + P·R·cos(90°- γ)·cos(90°) = Т·R.

М = Т·R.


Для вертикальной направляющей α = 90°.

М = Т·R·sin(90° + γ) + F_r·R·cos(90° + γ) + P·R·cos(90°)·cos(90° + γ) =

= Т·R·sin(90° + γ) + F_r·R·cos(90° + γ) = Т·R·cos(γ) - F_r·R·sin(γ) =

= Т·R·cos(γ) - P·sin(β)/sin(90° - β)·R·sin(γ) =

= Т·R·cos(γ) - P·R·sin(β)/cos(β)·sin(γ) = Т·R·cos(γ) - P·R·tg(β)·sin(γ).

М = Т·R·cos(γ) - P·R·tg(β)·sin(γ).


Для горизонтальной направляющей α = 0.

М = Т·R·sin(γ) + F_r·R·cos(γ) + P·R·cos(γ).

P·sin(α) = Т.

М = P·sin(0)·R·sin(γ) + F_r·R·cos(γ) + P·R·cos(γ) =

= F_r·R·cos(γ) + P·R·cos(γ).

Так как F_r/sin(β) = P/sin(α - β) будет

М = P·sin(β)/sin(0 - β)·R·cos(γ) + P·R·cos(γ) = 0.

21.10.2011 г. Исправлено 09.11.11 г.

...

Ответ начнем с места, где стоит вопрос 5.5.

Вопрос 5.5:

       Учитывая, что используется некруговая направляющая, Вы всё равно считаете, что момент вращения в указанной точке можно вычислять по формуле (3)?

Да. (мой правильный ответ – нет)

Ответ "нет" по той причине, что нарушается условие перпендикулярности R и T, в более общем случае некруговой направляющей. Запись от 21.10.11 г. (исправлено 09.11.11 г.) По этой причине появляется угол φ, который в случае окружности равен φ = 90°. Формула (3) требует обобщения на этот общий случай. ...

Вопрос 5.6:

       Таким образом, по Вашей методике получается, что совершенно независимо от того, как относительно оси ротора будет закреплена тяга (рисунок 3), момент ВСЕГДА следует вычислять по формуле (3). Значение имеет только положение груза относительно оси ротора.

Сравните вопросы 5.6 и 5.

Вопрос 5:

       Формула (3) никак не связана с существованием тяги, с существованием оси подвески этой тяги, с положением этой оси относительно оси ротора и с ориентацией тяги в координатах X-Y.

       Вы признаёте эти факты?

Здравствуйте Владимир Максимович. Ответ на вопрос 5 невозможно сформулировать только в виде, да или нет, так как это может привести в дальнейшем к неправильным выводам.

       Михаил, Ваша позиция мне понятна. Беру время на «помозговать».

Вопросы практически совпадают, однако далее Вы продолжаете настаивать на бинарном ответе, да или нет (зачем тогда было надо «помозговать»).

Ответ могу дать только расширенный.

       Ранее мной была записана последовательность выражений для случая направляющей окружности, рассмотрим её

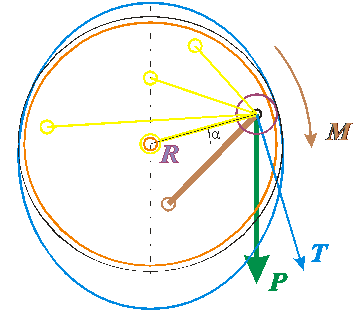
М = F_R·S = T/cos(α + β)·S = T/cos(α + β)·R·cos(α + β) = T·R.
Обратите внимание, что М = F_R·S, т. е. формально можно сказать, что момент зависит от положения тяги, так как F_R проходит через тягу. Однако далее видно, что в результате преобразований эта зависимость выпадает, т. е. остаётся только
М = T·R.
Поэтому с формальной математической точки зрения момент на роторе для окружной направляющей не зависит от параметров тяги, однако с практической точки зрения это не совсем так. Проблема в том, что в выражении для F_R есть особая точка. Это когда
α + β → 90°, и в этом случае
cos(α + β) → 0 и сила
F_R = T/cos(α + β) = P·cos(α)/cos(α + β) → ∞, стремится к бесконечности (заклинивание).
Практически это означает, что в конструкции возможно заклинивание, т. е. она не работоспособна при определённых математических параметрах, особенно при наличии трения. И этот вопрос требует особого изучения. В этом случае уже не работает, используемая в этой задаче геометрическая модель расчёта момента.

Для некруговой направляющей
М = F_R·S = Т·R·sin(θ)/sin(θ + δ), где δ – угол отклонения от окружной направляющей; θ – угол между радиусом и тягой. Из-за ненулевой величины δ появляется зависимость момента от угла между тягой и радиусом.

Вопрос 5.8:

       Поскольку по сути своей Ваша точка зрения осталась прежней, я продолжаю свою «тягомотину», полностью повторяя вопрос 5.6:

       Таким образом, по Вашей методике получается, что совершенно независимо от того, как относительно оси ротора будет закреплена тяга (рисунок 3), момент ВСЕГДА следует вычислять по формуле (3) или (4). Значение имеет только положение груза относительно оси ротора.

       Это так?

ПРИМЕЧАНИЕ
1.    На рисунке 3 другие произвольные положения тяги показаны в жёлтом цвете.
2.    Михаил, когда я читал лекции, то предупреждал своих Слушателей о том, что вопросы мои, как правило, содержат какого-нибудь поросёнка.
       При неверном ответе Слушателя я с удовольствием похрюкаю ему в ответ.

Задача Слушателя – постараться лишить меня этого удовольствия.

Рис. 3

радиус R зависит от угла γ.

Вопрос 5.9:

1.    «ХРЮ-ХРЮ!»

       Радиус R не может зависеть от какого-либо угла! Это – чистый нонсенс, так как расстояние от оси ротора до центра груза – величина конструктивно-жёсткая и потому – не зависит от ориентации тяги.
       В этом случае всегда R = const, и направляющая будет только круговой. Так как Вы объявили, «Считайте теперь, что направляющая у нас - НЕ круговая ...», и соответственно этим определили, что радиус движения груза будет переменной величины, т. е. зависит от угла γ при обходе контура направляющей. Груз, перемещающийся по некруговой направляющей будет менять своё расстояние от оси ротора, если не имеется ввиду, что ось ротора или сама направляющая поступательно подвижны, а это не оговаривалось. Мои заявления соответствуют поставленной задаче.

2.    Ваш ответ на вопрос 5.8 (а, следовательно – и на вопрос 5.6) не соответствует формату «ДА – НЕТ».

Поэтому в третий раз повторяю вопрос 5.6:

       По Вашей методике получается, что совершенно независимо от того, как относительно оси ротора будет закреплена тяга (рисунок 3), момент ВСЕГДА следует вычислять по формуле (3) или (4). Значение имеет только положение груза относительно оси ротора.

       Это так?

ПРИМЕЧАНИЕ

1.    На рисунке 3 другие произвольные положения тяги показаны в жёлтом цвете.
2.    Любой момент вращения – это произведение силы на расстояние от неё до оси вращения.

            Чем дальше Вы углубляетесь в математику, тем, соответственно, дальше отдаляетесь от этой логики.

Вопрос 5.10:

       Михаил, после Вашего изменения ответа на вопрос 5.5 с «ДА» на «НЕТ» я подождал Вашего указания на дополнительный угол.
       Вы этот угол назвали (ответом на вопрос 5.7).

М = Т·R·sin(φ) = Т·R·sin(180° - α - γ) = Т·R·sin(α + γ), так как α + γ + φ = 180°.
При φ = 90° имеем частный случай с окружностью.

Новая формула изменяет величину момента, но не изменяет сути – для круговой направляющей новая формула полностью повторяет формулу (4).
       В формуле (4) отсутствует информация о наличии тяги, об её ориентации и о положении оси подвески этой тяги относительно оси ротора.
       Поэтому вопрос 5.6 был оставлен мною без изменений (под номером вопрос 5.8).

       В ответе на вопрос 5.8 Вами выданы достаточно капитальные математические выкладки, но не было конкретного высказывания ни «ДА», ни «НЕТ». И помимо того, что не было дано односложного ответа, в Вашем ответе был явный ляп, относящийся к зависимости величины R от какого-то угла.
Мои заявления соответствуют поставленной задаче. γ – угол между осью x и радиусом R.

       Я убедительно просил Вас отвечать либо «ДА», либо «НЕТ», кроме редких случаев, когда такими ответами действительно нельзя обойтись.
       На Ваше «НЕТ» я бы мог разделить новую проблему на короткие части и задать какой-нибудь соответствующий вопрос, допускающий ответ в формате «ДА» или «НЕТ».
       На мой вопрос 5.9 Вы опять не смогли ответить ни «ДА», ни «НЕТ».
       Поэтому сейчас я снова, в четвёртый раз задаю тот же вопрос, какой задавался вопросом 5.6:

       По Вашей методике получается, что совершенно независимо от того, как относительно оси ротора будет закреплена тяга (рисунок 3), момент ВСЕГДА следует вычислять по формуле (3) или (4). Значение имеет только положение груза относительно оси ротора.

       Это так?

ПРИМЕЧАНИЕ

1.    На рисунке 3 другие произвольные положения тяги показаны в жёлтом цвете.
2.    Любой момент вращения – это произведение силы на расстояние от неё до оси вращения.
       Чем дальше Вы углубляетесь в математику, тем, соответственно, дальше отдаляетесь от этой логики
       Формула М = F_R·S, справедлива для любой тяги нарисованной Вами, где S – расстояние от неё до оси вращения. Поэтому ваше утверждение не соответствует действительности. Если тяга совпадает с радиусом, то в этом случае требуется особое рассмотрение этой задачи. Это особая математическая точка S → 0. При этом S → 0 и S = 0 не одно и то же с математической точки зрения. Здесь разрыв функции и требует исследования.

3.    Михаил, меня не пугает возможность получить неприятную информацию. Я очень хочу понять причину, мешающую мне принять Ваши выводы.
       На моей стороне – логика физических процессов. На Вашей стороне – логика абстрактной математики.
       Нет, Владимир Максимович. На моей стороне логика триединства: опыт, математика, физика, замкнутые в кольцо. Они находятся в согласии, а не противоречии как у вас.

       В одном из более ранних наших обменов мнениями я пытался показать Вам, что математика – это всего лишь инструмент. И применять его следует к месту. В конце концов, микроскоп, например, тоже является инструментом, но, если им забивать гвозди, то положительный результат таки будет достигнут. Да только в душе останется осадок неполной удовлетворённости.
       С Вашей точки зрения интеграл от полуокружности равен нулю. А с моей точки зрения – площадь полукруга не может равняться нулю.
       И это совсем не с моей точки зрения, а с точки зрения общепринятых принципов математики, которыми вы упорно пренебрегаете. Вычисление площади это только частный случай применения интеграла. В этом случае площадь будет всегда положительной, однако в общем случае часть интеграла может быть и отрицательной, поэтому в сумме возможен 0. При нахождении интегральной суммы нельзя ставить знаки по принципу, как мне видится. Знаки определяются математической логикой, и это соответствует опыту.

         Я могу согласиться с тем, что ошибка кроется в моих взглядах. Но для этого я должен эту ошибку увидеть и понять её.
        Если ошибка есть результат неправильных взглядов, то единственный способ её устранения это изменение взглядов, а понимание придёт в процессе применения принципов, которые Вы считаете не убедительными.

       То, что более правильной является Ваша позиция, для меня пока не является убедительным доводом. Для меня останется очевидным и убедительным реальный (хотя бы и умственно воспроизводимый) физический процесс, даже если результат противоречит математике.
        Правильная теория не может противоречить математической логике, ибо это противоречие делает невозможным правильные вычисления в пределах этой теории. Результаты подобных вычислений практически всегда будут абсурдны. Наш мир принципиально счётен, по определённым правилам, которые далеко не очевидны с точки зрения гуманитарной логики и математика есть отражение этого факта.

С уважением, Михаил.

07.11.2011 г.

Комментарии к измерениям момента для схемы

Масса груза Р = 285 гр.
Радиус равен R = 128 мм.
Радиус точек приложения безмена равен 110 мм.
Угол усреднения равен 60° относительно горизонтальной оси в первой четверти.

Из таблицы можно вычислить радиус рычага безмена
33792,0/307,2 = 110 мм.

Из таблицы можно вычислить вес груза
33792,0/118,57 ≈ 285 гр.

Коэффициент усреднения из таблицы при измерении равен
33792,0/285/128 = 0,9263

Для вычисления среднего теоретического момента на интервале поворота используем формулу для окружной направляющей
M_R = T·R = P·R·cos(α).

Интеграл от момента равен
P·R·sin(α).

На интервале 0 – 60° коэффициент усреднения будет равен (значение интеграла на интервале разделить на интервал в радианах)
sin(60°)/(60°·π/180°) ≈ 0,827.

Средний момент на интервале 0 – 60° равен
М_усредн = 0,827·285·128 = 30168,72. Это значение отличается от измеренного на -12%. Эта погрешность могла появиться из-за завышения коэффициента усреднения при обработке дискретных значений момента при измерении с шагом 10°. Сравните 0,9263 и 0,827. С учётом этого видно, что теоретическое значение момента полностью совпадает с измеренным.

Другие возможные причины наблюдаемой погрешности в 12%.

1. Трение деталей. Погрешность от трения может иметь любой знак. Знак зависит от направления последнего относительного сдвига деталей при измерении.

2. Применение резиновых безменов. Точность их работы зависит от истории деформаций и температуры.

С уважением, Михаил.

09.11.2011 г.

Оглавление

Продолжение

Назад

Главная страница