| |
Результаты моделирования инерцоида.
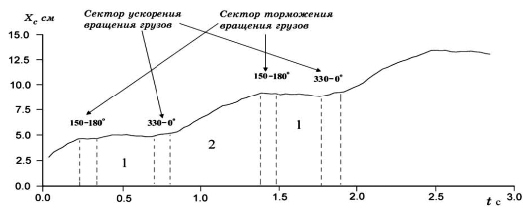
Эта серия графиков движения инерцоида выполнена при одинаковых параметрах и настройках механизма. Графики прорисованы от начала движения с медленного полутакта. По оси «x» время в секундах. Их можно сравнивать количественно. Теория с помощью которой построены эти графики со временем будет изложена на странице «Динамика». Соблюдается закон сохранения энергии. Закон сохранения импульса в классическом варианте не соблюдается. Силы инерции работы не совершают. Происходит преобразование внутренней энергии инерцоида в поступательную энергию центра масс. Движение инерцоида происходит по нелинейным законам механики.
Полная масса инерцоида m = 0,95 кг.
Масса грузов m2 = 0,26 кг (2·0,13 кг), т. е. я, использовал не симметричную модель, так как при численном моделировании это удобнее. Вся масса сосредоточена в одном грузе это соответствует модели Толчина с массой одного груза 0,13 кг.
Масса корпуса m1 = 0,69 кг.
Длина стержня R = 60 мм.
Момент (фактически сила, приложенная непосредственно к грузу со стороны механизма):
в медленном полутакте +6 грамм;
в быстром полутакте +10 грамм.
В этом опыте считаем, что привод грузов выдаёт практически постоянный момент не зависящий от полутакта и времени работы, однако трение мотор-тормоза в медленном полутакте уменьшает момент. В реальном пружинном инерцоиде сила привода уменьшается при раскручивании пружины.
Трение в колёсах 1 грамм. Нелинейность трения не задана.
Жесткость стержня, соединяющего грузы и корпус 5 тон/мм.
Начальная скорость грузов в медленном полутакте 0,12 м/с.
Начальная скорость грузов в быстром полутакте в шесть раз больше 0,72 м/с.
Переключение скорости грузов, т. е. имитация мотор-тормоза, происходит в каждом полутакте при 0 и 180° градусах мгновенно с соответствующим учётом энергии движения. Тактовый период 1 сек.

Сравните движение виброхода (ст. 4 сайта) и инерцоида при трении в 1 грамм. Траектория грузов приближается к форме, которую нарисовал Толчин (рис. 10).

Действительно, рассматривая работу инерцоида, многие не обращают внимания, на то, что геометрический центр вращения системы в быстром полутакте значительно ближе к грузам, чем это следует из принятых представлений о движении центробежного вибратора. Толчин даже изобразил это в своей книге на рисунке. Видимо надеясь, что это примут как экспериментальный факт, а не как галлюцинации шизофреника. И этот факт непосредственно подтверждается слишком несоразмерным шагом инерцоида в быстром полутакте, т. е. 90 мм это почти в три раза больше амплитуды (2,74 раза).
А вот медленном полутакте откат корпуса назад незначительно меньше амплитудного значения B = 32,84 мм, т. е. примерно 30 мм. Что может быть только при очень малом трении и говорит только о том, что импульс от трения мало влияет на движение корпуса и соответственно кинетическая энергия центра масс мала в конце медленного полутакта (рассуждаем с классической позиции). Фактически медленный полутакт мало отличается от полутакта свободного вибратора (всего на 2,84 мм (8,65%), может несколько больше, что все равно мало). При частоте работы механизма в 1 Гц скорость центра масс свободного вибратора в этом случае была бы соответственно 2,84 мм/с относительно конца фазы отката назад. Такая энергия не способна повлиять на процессы в быстром полутакте, т. е. медленный и быстрый полутакты практически независимы. Обратите внимание, что импульс от трения в быстром полутакте значительно меньше и направлен против движения, и он влияет на медленный полутакт соответственно ещё меньше.
Необходимо чётко видеть, что при указанном влиянии силы трения на колебательный процесс, перемещение грузов относительно внешней системы отсчёта может быть деформировано только в пределах нескольких миллиметров, и поэтому ни какого перемещения корпуса в быстром полутакте в пределах 90 мм не может быть в принципе при соблюдении классических законов. Надо видеть, что роль трения в быстром полутакте значительно меньше, чем в медленном полутакте и трение всегда только уменьшает амплитуду колебаний корпуса вибратора и поэтому предположения, что трение может увеличить амплитуду корпуса в быстром полутакте, выглядит совершенно неправдоподобно. Однако многих теоретиков это совершенно не смущает, как ни странно, они считают, что деформацию траектории грузов, наблюдаемую в опыте можно списать на внешнее трение (внутренние силовые факторы по классическим канонам в принципе не могут так сильно изменить амплитуду колебаний центробежного вибратора с фиксированным по длине рычагом).
| Откат. |
-49,39 |
-37,49 |
-30,01 |
-24,91 |
| Ход вперёд. |
76,10 |
83,39 |
90,00 |
95,85 |
| Ход за такт. |
26,71 |
45,90 |
59,99 |
70,94 |
Из таблицы и графика видно, что при увеличении средней скорости центра масс на графике перемещения центра масс формируется горизонтальная площадка. В этой зоне параметры перемещения приблизительно такие же, как и у пружинного инерцоида (четвёртый столбец). Среднее от соседних столбцов (3 и 5), дают почти те же числа (-31,02; 89,62; 58,42). Программная модель в динамике ведет себя несколько иначе. Медленнее разгоняется и не достигает режима стабилизации скорости, что скорее всего связано с другим режимом работы механизма. Со временем попробую это исправить подбором алгоритма работы кинематики. Обратите внимание, что перемещение центра масс происходит в быстром полутакте, а не в медленном как у виброхода. Это соответствует опыту.

Назад

Оглавление
|
|








