|
Комментарий к публикациям Трещалова Германа Владиславовича, с изложением физического содержания в моей форме понимания. http://erg.ucoz.org/pub/info/Hydrodynamic_Effect_ru.pdf http://erg.ucoz.org/pub/info/Modelling_Effect_ru.pdf Гидравлика под ред. проф. И. И. Агроскина. Трансформация полной энергии потока воды. Рассмотрим изменение удельной энергии в потоке прямоугольного сечения в зависимости от высоты при условии \( \displaystyle L \cdot H \cdot w = Q \), где
\( \displaystyle L = const \). \( \displaystyle ρ w \cdot dw + ρ g \cdot dH = de. \) \( \displaystyle L H w = Q.~~~~ \) Объёмный расход. Дифференцируем \( \displaystyle L H \cdot dw + L w \cdot dH = 0;~~~~ \) \( \displaystyle H \cdot dw + w \cdot dH = 0. \) \( \displaystyle dw = - w \frac{dH}{H};~~~~ \) \( \displaystyle - ρ w^2 \cdot \frac{dH}{H} + ρ g \cdot dH = de;~~~~ \) \( \displaystyle - \frac{ρ w^2}{H} + ρ g = \frac{de}{dH};~~~~ \) \( \displaystyle ρ g \left(1 - \frac{w^2}{g H} \right) = \frac{de}{dH};~~~~ \) \( \displaystyle ρ g \left(1 - Fr^2 \right) = \frac{de}{dH} > 0 \) в диапазоне \( \displaystyle 0 < Fr < 1.~~~~ \) Обратите внимание, что в рассматриваемом потоке \( \displaystyle d H < 0 \), т. е. высота по направлению потока уменьшается. ... Наличие максимума мощности при числе Фруда \( \displaystyle Fr = 0.30937 \) напрямую связано с выбором условия неразрывности потока в виде
\( \displaystyle \frac {ρ w^2}{2} + ρ g H = e = const. \) (4) Удельная энергия потока во всех сечениях постоянна. Дифференцируем (4) \( \displaystyle ρ w \cdot dw + ρ g \cdot dH = 0;~~~~ \) \( \displaystyle w \cdot dw + g \cdot dH = 0. \) \( \displaystyle H L w = Q = const. \) (5) Объёмный расход во всех сечениях постоянный. Дифференцируем (5) \( \displaystyle H L dw + w H dL + w L dH = 0;~~~~ \) \( \displaystyle \frac {dw}{w} + \frac {dL}{L} + \frac {dH }{H} = 0 \). \( \displaystyle \frac {H L dw}{Q} + \frac {dL}{L} + \frac {dH }{H} = 0;~~~~ \) \( \displaystyle -\frac {H L g \cdot dH}{Qw} + \frac {dL}{L} + \frac {dH }{H} = 0;~~~~ \) \( \displaystyle -\frac {g H^2 L^2 \cdot dH}{Q^2} + \frac {dL}{L} + \frac {dH }{H} = 0 \). \( \displaystyle -\frac {g S^2 \cdot dH}{Q^2} + \frac {dS}{S} = 0;~~~~ \) \( \displaystyle -\frac {g S^3}{Q^2} + \frac {dS}{dH} = 0 \). Здесь обобщаем, считая, что можно записать \( \displaystyle \frac {dS}{S} = \frac {dL}{L} + \frac {dH}{H} \) и \( \displaystyle S = H L \). \( \displaystyle \frac {dS}{dH} = \frac {g}{Q^2} S^3 \). Это частный случай дифференциального уравнения Бернулли \( \displaystyle y^{'} + P(x) \cdot y = Q(x) \cdot y^n.~~~~ \) Делим на \( \displaystyle S^3 \). \( \displaystyle \frac {1}{S^3} \frac {dS}{dH} = \frac {g}{Q^2} \). Заменяем переменную \( \displaystyle Z = S^{-2};~~~~ \) \( \displaystyle Z^{- \frac{1}{2}} = S;~~~~ \) \( \displaystyle Z^{ - \frac{3}{2}} = S^3 \). \( \displaystyle - \frac{1}{2} Z^{ - \frac{3}{2}} \cdot \frac{dZ}{dH} = \frac{dS}{dH} \). \( \displaystyle - \frac {1}{Z^{-\frac{3}{2}}} \frac{1}{2} Z^{ - \frac{3}{2}} \cdot \frac{dZ}{dH} = \frac {g}{Q^2} \). \( \displaystyle - \frac{1}{2} \frac{dZ}{dH} = \frac {g}{Q^2};~~~~ \) \( \displaystyle \frac{dZ}{dH} = - \frac {2g}{Q^2} \). Интегрируем на интервале изменения высоты сечения \( \displaystyle Z - Z_0 = - \frac {2g}{Q^2} (H - H_0) \). \( \displaystyle \frac{1}{S^2} - \frac{1}{S_{0}^2} = - \frac {2g}{Q^2} (H - H_0); \) \( \displaystyle \frac{1}{S^2} = - \frac {2g}{Q^2} (H - H_0) + \frac{1}{S_{0}^2};~~~~ \) \( \displaystyle \frac{1}{S} = \sqrt{ - \frac{2g (H - H_0)}{Q^2} + \frac{1}{S_{0}^2}}; \) \( \displaystyle S = \frac {1}{\sqrt{ - \frac{2g (H - H_0)}{Q^2} + \frac{1}{S_{0}^2}}} \). \( \displaystyle S = \frac {Q}{\sqrt{ 2g (H_0 - H) + w_{0}^2}} = \frac {S_0 \cdot w_{0}}{\sqrt{ 2g (H_0 - H) + w_{0}^2}} = \frac {S_0 \cdot w_{0}}{\sqrt{ 2g \Delta H + w_{0}^2}} \). (6) В результате длинных вычислений мы получили простую зависимость площади сечения от перепада высот, до которой можно было догадаться и так, но в данном случае важно, что \( \displaystyle w = \sqrt{ 2g \Delta H + w_{0}^2} \). (7) Подстановкой в (4) и (5) можно проверить формулы (6), (7). Формула (7) для случая, когда скоростью потока в сосуде уже пренебречь нельзя, т. е. не соблюдается условие, Обратите внимание, что переход потока от меньшей высоты к большей за счёт собственной энергии возможен только при условии, \( \displaystyle S = \frac {S_0 \cdot w_{0}}{\sqrt{ w_{0}^2 - 2g \Delta H}} \). При \( \displaystyle w_{0}^2 = 2g \Delta H \) выходная площадь равна бесконечности и давление перехода равно давлению торможения входного потока. 08.11.2013 г Рассмотрим числовой пример подобного преобразования при заданных параметрах в следующем техническом варианте. \( \displaystyle k_p = \frac{ w_{0}^2 + 2g \Delta H }{ w_{0}^2 + 2g H_0} \) \( \displaystyle = 0.714 \). \( \displaystyle k_{pd} = k_o \cdot k_м \cdot k_к \cdot k_p \) \( \displaystyle = 0.543 \). Мощность \( \displaystyle k_{pd} Q \left( \frac{ρ w_{0}^2}{2} + ρ g H_0 \right) \) \( \displaystyle ≡5.597 ~кВт \). Рассматривая подобные задачи, необходимо иметь в виду, что получить расчётную мощность можно только при наличии возможности отвода отработанного потока из турбины. ...
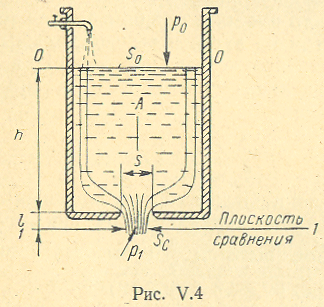
Докажем формулу (7) для случая истечения из донного отверстия.
Для определения скорости истечения из сосуда будем считать, жидкость идеальной \( \displaystyle \frac {ρ V_{0}^2}{2} + ρ g z_{0} + p_{0} = \frac {ρ V_{1}^2}{2} + ρ g z_{1} + p_{1}; \) \( \displaystyle \frac {ρ V_{0}^2}{2} + ρ g z_{0} - ρ g z_{1} + p_{0} - p_{1} = \frac {ρ V_{1}^2}{2}; \) \( \displaystyle \frac {ρ V_{1}^2}{2} = \frac { ρ V_{0}^2}{2} + ρ g( z_{0} - z_{1}) + p_{0} - p_{1}. \) Так как \( \displaystyle p_{0} - p_{1} = 0 \) и \( \displaystyle z_{0} - z_{1} = \Delta h \), то \( \displaystyle \frac {ρ V_{1}^2}{2} = \frac { ρ V_{0}^2}{2} + ρ g \Delta h \); \( \displaystyle V_{1}^2 = V_{0}^2 + 2g \Delta h \); \( \displaystyle V_{1} = \sqrt{ V_{0}^2 + 2g \Delta h}. \) (1) Если \( \displaystyle S_{0} >> S \), то скоростью \( \displaystyle V_{0} \) можно пренебречь и останется формула Торричелли. \( \displaystyle V_{1} = \sqrt{ 2g \Delta h}. \) Фомула Торричелли это частный случай формулы (1) при \( \displaystyle S_{0} >> S \). ... Михаил Ost. Редакция от 26.08.2013 г; 08.11.2013 г.
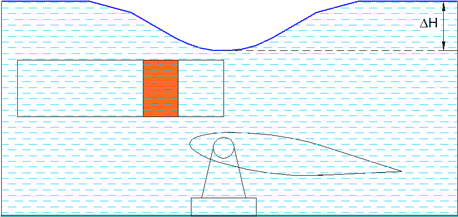
Коэффициент усиления можно выразить через число Фруда, относительно входного потока. \( \displaystyle K = k_0 \cdot k_p \cdot \left(1 + \frac{2}{Fr_{v}^2} \right) \), где \( \displaystyle Fr_{v} = \frac{w_0}{\sqrt{g \cdot H_0 }}. \) ... Схема турбины с трансформацией потока, сводится к более простой эквивалентной схеме, в которой используется перепад давлений между входом и выходом трубы. В трубу помещается турбина, работающая на постоянной скорости потока, без расширения. Перепад давлений создаётся за счёт потенциальной ямы, формируемой крылом. Циркуляция вокруг крыла обеспечивает разность скоростей между дном и поверхностью. Эта схема более экономична, так как исключается повышенная скорость потока в тракте турбины. Кривая поверхность тока воды создаёт те же условия отвода отработанной воды, что и горизонтальная. В работе турбины принимает участие значительно большая масса воды, чем проходящая через неё.
Мощность турбины приблизительно равна \( \displaystyle \Delta p ~ Q = ρ ~ g ~ \Delta H ~ S_0 ~ w_0. \) Коэффициент усиления по мощности относительно входного потока \( \displaystyle K = \frac{2 g ~ \Delta H }{w_0^2} = \frac{2}{Fr_{ \Delta H}^2} \), где \( \displaystyle Fr_{\Delta H} = \frac{w_0}{\sqrt{g ~ \Delta H }} \). 13.11.2013 г.
Найдём приблизительную зависимость мощности турбины от параметров крыла, формирующего потенциальную яму на поверхности воды. Подъёмная сила крыла равна \( \displaystyle F = \frac{1}{2} ρ ~ C_y ~ w_0^2 ~ S_k. \) Среднее давление на поверхность крыла \( \displaystyle p = \frac{F}{S_k} = \frac{1}{2} ρ ~ C_y ~ w_0^2. \) В рассматриваемом случае нас интересует пониженное давление на верхней половине крыла. По этой причине коэффициент подъёмной силы \( \displaystyle C_y \) будет отличаться от принятого в аэродинамике и потребует специального расчёта. В этом варианте коэффициент подъёмной силы зависит не только от числа Рейнольдса, угла атаки, но и от расположения крыла в потоке, его глубины. \( \displaystyle p = \frac{1}{2} ρ ~ C_y ~ w_0^2 = ρ ~ g ~ \Delta H; ~\) \( \displaystyle \frac{1}{2} ~ C_y ~ w_0^2 = g ~ \Delta H. \) \( \displaystyle Fr_{ \Delta H} = \sqrt{\frac{2}{C_y}}. \) \( \displaystyle K = C_y. \) \( \displaystyle \Delta H = \frac{1}{2~g} C_y ~ w_0^2. \) Мощность равна \( \displaystyle N = ρ ~ g ~ \Delta H ~ S_0 ~ w_0 = ρ ~ g ~ \frac{1}{2~g} C_y ~ w_0^2 ~ S_0 ~ w_0 = \frac{1}{2} ρ ~ C_y ~ w_0^3 ~ S_0. \) Расчёты справедливы при длине крыла больше глубины и значительно больше диаметра турбины. ... Редакция от 18.11.2013 г. Михаил Ost.
Рассмотрим ошибку Дмитрия Борисовича Зотьева, допущенную им при вычислении потока энергии через замкнутую поверхность, в работе Лженаука атакует. (Доктор физ-мат наук , профессор кафедры общей физики ВФ МЭИ, Зотьев Д.Б.)
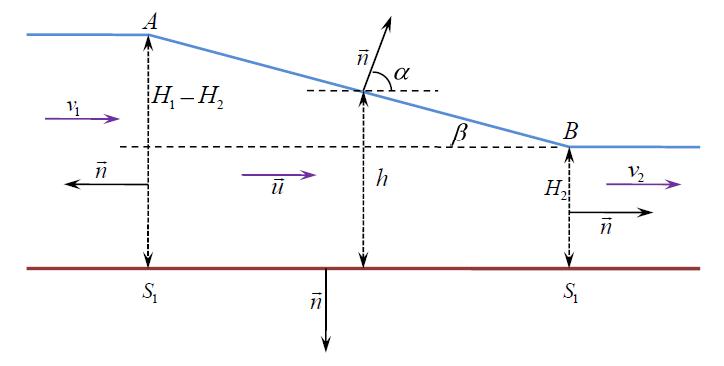
Внимательно посмотрите на рисунок, взятый из его статьи.
Обратите внимание, что угол \( \displaystyle \alpha \) для вычисления скалярного произведения в интеграле потока отсчитывается от линии параллельной дну. Это связано с тем, что автор делает неверное предположение о структуре векторного поля между сечениями \( \displaystyle S_1 \) и \( \displaystyle S_2 \). Отрезок AB это линия тока. Нормаль к поверхности перпендикулярна этой линии и скорости соответственно. В этом случае скалярное произведение на наклонной поверхности \( \displaystyle \vec u \cdot d \vec S = 0 \). Потока энергии через поверхность определяемую отрезком AB нет. Это очевидно и без вычислений, из элементарных физических соображений. Поэтому поток энергии надо вычислять только через поверхности \( \displaystyle S_1 \) и \( \displaystyle S_2 \). Рассмотрим стационарный поток с произвольным распределением скорости в сечениях. Ширина потока постоянна и равна \( \displaystyle L \). Поток энергии равен \( \displaystyle \int \limits_{~~~~~~S_2} \int \left( \frac{\rho u_{2}^2}{2} + \rho g h + P_2 \right) \vec u_2 \cdot d \vec S + \int \limits_{~~~~~~S_1} \int \left( \frac{\rho u_{1}^2}{2} + \rho g h + P_1 \right) \vec u_1 \cdot d \vec S = \) \( \displaystyle = \int \limits_{~~~~~~S_2} \int \left( \frac{\rho u_{2}^2}{2} + \rho g h + P_2 \right) u_2 \cdot d S - \int \limits_{~~~~~~S_1} \int \left( \frac{\rho u_{1}^2}{2} + \rho g h + P_1 \right) u_1 \cdot d S = \) Так как \( \displaystyle P_2 = \rho g (H_2 - h) \); \( \displaystyle P_1 = \rho g (H_1 - h) \) в продолжении будет \( \displaystyle = \int \limits_{0}^{H_2} \left( \frac{\rho u_{2}^2}{2} + \rho g H_2 \right) L \cdot u_2 \cdot d H - \int \limits_{0}^{H_1} \left( \frac{\rho u_{1}^2}{2} + \rho g H_1 \right) L \cdot u_1 \cdot d H = \) \( \displaystyle = \int \limits_{0}^{H_2} \frac{\rho u_{2}^2}{2} L \cdot u_2 \cdot d H + \rho g H_2 \cdot Q - \int \limits_{0}^{H_1} \frac{\rho u_{1}^2}{2} L \cdot u_1 \cdot d H+ \rho g H_1 \cdot Q = \) \( \displaystyle = Q \left( \int \limits_{0}^{H_2} \frac{\rho u_{2}^2}{2Q} L \cdot u_2 \cdot d H + \rho g H_2 \right) - Q \left( \int \limits_{0}^{H_1} \frac{\rho u_{1}^2}{2Q} L \cdot u_1 \cdot d H+ \rho g H_1 \right) = \) \( \displaystyle = Q \left( \frac{\rho u_{q2}^2}{2} + \rho g H_2 \right) - Q \left( \frac{\rho u_{q1}^2}{2} + \rho g H_1 \right) = \frac{dE}{dt} \), где \( \displaystyle u_{q2};~~ u_{q1} - \) среднеквадратические скорости в сечениях \( \displaystyle S_2 \) и \( \displaystyle S_1;~~ \) \( \displaystyle Q - \) объёмный расход. Михаил Борисович Ост. 01.01.2014 г.
Автор написал новый вариант статьи Лженаука атакует. И частично признал свои ошибки. Форум ФИАН. Работа Соколова http://arxiv.org/abs/1312.5780 Для несжимаемой среды дифференциал \( \displaystyle p \cdot dV = 0, \) т. е. упругая энергия равна нулю. Поэтому списать разность \( \displaystyle \frac{MgH_1}{2} - \frac{MgH_2}{2} \) на упругую энергию невозможно. Дифференциал работы сил давления с учётом сжимаемости равен \( \displaystyle dA = d(pV) = p~ dV + dp~ V \). В идеальной несжимаемой жидкости останется только слагаемое \( \displaystyle dp~ V = dA \), т. е. жидкость движется в градиенте давления. Поэтому действие гидростатического давления связано не только с механическим сжатием объёма, но и с его движением в градиенте гидростатического давления. 04-05.02.2014 г.
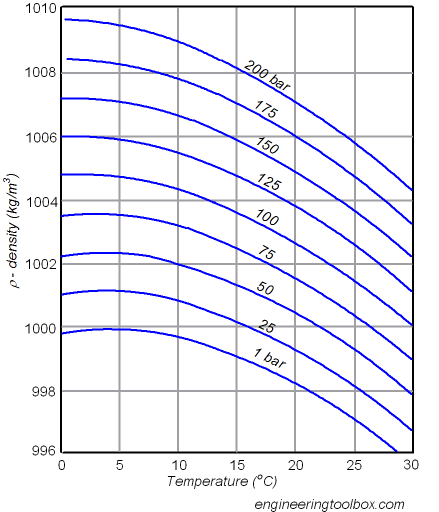
Плотность воды на глубине 250 метров увеличивается примерно на 0.1%.
Найдём из приведённой диаграммы среднюю величину производной \( \displaystyle \left( \frac{\partial \rho}{\partial p} \right)_{15 °С} \) в диапазоне 1 ÷ 200 Bar. \( \displaystyle \left( \frac{\partial \rho}{\partial p} \right)_{15 °С} = 4,559 \cdot 10^{-7} \frac{кг}{м^3 \cdot Па} \). Так как \( \displaystyle dA = p_0 ~ dV;~ \) \( \displaystyle dm = \rho ~ dV \), тогда \( \displaystyle \frac{dA}{V} = p_0 \frac{dV}{V} = d e;~ \) \( \displaystyle \frac{dm}{V} = \rho \frac{dV}{V} = d \rho \). \( \displaystyle d e = \frac{p_0}{\rho} d \rho \). Для оценки изменения удельной энергии можно записать \( \displaystyle \Delta e = \frac{p_0}{\rho} \Delta \rho = \frac{p_0}{\rho} \left( \frac{\partial \rho}{\partial p} \right)_{15 °С} \Delta p = \frac{p_0}{\rho} \left( \frac{\partial \rho}{\partial p} \right)_{15 °С} \rho g \Delta h = g~ p_0 \left( \frac{\partial \rho}{\partial p} \right)_{15 °С} \cdot \Delta h \). \( \displaystyle p_0 = 1,01325 \cdot 10^5~Па - \) атмосферное давление. \( \displaystyle \Delta e = 9.80665~ \frac{м}{с^2} \cdot 1,01325 \cdot 10^5~Па \cdot 4,559 \cdot 10^{-7} \frac{кг}{м^3 \cdot Па} \cdot 1~ м = 0,453 \frac{Дж}{м^3} \). При изменении глубины на один метр и атмосферном давлении, удельная энергия воды изменяется на \( \displaystyle 0,453 \frac{Дж}{м^3} ≡ 0,046~ мм~ вод. ст. \) Обратите внимание, что производная \( \displaystyle \left( \frac{\partial \rho}{\partial p} \right) \) от давления зависит незначительно. В рассматриваемом диапазоне давлений вода на сжатие, имеет практически постоянный коэффициент модуля упругости (при фиксированной температуре). 09.02.2014 г. Михаил Борисович Ост. Продолжение следует. Гидравлика под ред. проф. И. И. Агроскина. Вопросы можно задавать на форуме Трансформация полной энергии потока воды. Оглавление сайта
|
||

Механика инерцоида
| ||
| Главная | Трансформация полной энергии потока воды | Мой профиль | Выход | Вы вошли как Гость | Группа " Гости" | RSS |  |