|
«В 1879 году В. Томсон и П. Тет [85] наметили ещё одно, третье направление, состоящее в следующем. Уравнения движения системы, в составе которой имеются гироскопы, содержат линейные относительно скоростей члены с кососимметричной матрицей коэффициентов. Если эти члены трактовать как силы, то их работа на действительном перемещении системы будет равна нулю. Это свойство Томсон и Тет приняли за общее определение гироскопических сил и, пользуясь им, доказали несколько теорем об устойчивости движения гироскопических систем.»
Меркин Д. Р., Гироскопические системы, "Наука", 1974, ст. 8.
«Гироскопические силы в понимании Томсона и Тета встречаются не только в системах, содержащих гироскопы, но также в различных механических, электрических и других системах, в которых гироскопы отсутствуют. Поэтому между системами самой различной физической природы можно провести далеко идущие аналогии, которые можно использовать в различных конструкциях.»
Меркин Д. Р., Гироскопические системы, "Наука", 1974, ст. 10.
«Общее определение гироскопических сил
Силы Г1, Г2, ..., Гn называются гироскопическими, если сумма их работ на действительном перемещении dr1, dr2, ..., drn системы равна нулю (определение Томсона и Тета).
Заметим, что гироскопические силы могут быть как действительными силами, приложенными к системе, так и просто некоторыми членами уравнений движения, которые удобно трактовать как силы. Поэтому, употребляя термин "гироскопические силы", нужно помнить его условный характер. По этой же причине очень часто гироскопические силы называют гироскопическими членами (мы будем употреблять оба термина).»
Меркин Д. Р., Гироскопические системы, "Наука", 1974, ст. 11.
«Р е а к ц и и и д е а л ь н о й с в я з и. Из общего определения гироскопических сил следует, что они обладают свойством реакций идеальных связей.
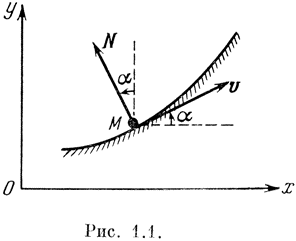
Покажем на простейшем примере, что реакции таких связей имеют гироскопическую структуру.
Пусть материальная точка М массы m движется по некоторой неподвижной гладкой кривой, расположенной в плоскости xy (рис. 1.1). Обозначим через N реакцию связи и через v – скорость точки (активные силы нас сейчас не интересуют). Так как сила N перпендикулярна к скорости v (кривая по условию гладкая и, следовательно, реакция кривой направлена по нормали), то скалярное произведение векторов N и v (мощность силы N) равно нулю:
N·v = 0.
Таким образом, сила удовлетворяет условию (1.1), т. е. она подпадает под общее определение гироскопических сил.
Найдем проекции этой силы на оси координат. Пользуясь рис. 1.1, получим
Nx = - N sin α, Ny = - N cos α,
где N – модуль силы N, α – угол между скоростью v точки М и осью x.
За обобщённые координаты точки М возьмём её декартовы координаты x и y.
Тогда проекции Nx и Ny будут соответствующими обобщёнными гироскопическими силами. Имеем: cos α = vx /v, sin α = vy /v.
Подставляя эти значения для cos α и sin α в выражения для Nx и Ny, получим гироскопические силы, записанные в форме (1.4):
Nx = - N/v·vy,
Ny = - N/v·vx.
Отсюда находим гироскопические коэффициенты:
g11 = g22 = 0, g12 = - g21 = - N/v.
Матрица, составленная из этих коэффициентов,
| 0 - N/v |
G = | |
| N/v 0 |
в соответствии с общей теорией – кососимметричная.
В общем случае гироскопические силы Nx и Ny нелинейны, так как коэффициенты g12 и g21 зависят от скоростей vx и vy ( v 2 = vx2 + vy2 ).»
Меркин Д. Р., Гироскопические системы, "Наука", 1974, ст. 17-18.
«Д в и ж е н и е м а т е р и а л ь н о й т о ч к и в р а в н о м е р н о в р а щ а ю щ е й с я
с и с т е м е к о о р д и н а т. Предположим, что движение точки М изучается относительно системы координат x, y, z, вращающейся с постоянной по величине и направлению скоростью ω. Положение точки в системе x, y, z будем определять относительным радиус-вектором
r(x, y, z). Тогда вектор относительной скорости точки vr будет равен
vr = vxi + vyj + vzk,
где i, j и z – единичные орты вращающихся осей координат. Переносная скорость точки согласно теореме Эйлера равна
ve = ω × r.
Полная (абсолютная) скорость точки будет
v = vr + ve,
и следовательно, её кинетическая энергия равна
T = ½ m (vr + ve)·(vr + ve),
где m – масса точки. Раскроем это скалярное произведение и произведём очевидные преобразования:
T = ½ m (vr + ve)·(vr + ve) = ½ m (vr2 + 2vr·ve + ve2) =
= ½ m [(vx2 + vy2 + vz2) + 2vr·(ω × r) + (ω × r)2] =
= ½ m (vx2 + vy2 + vz2) +
+ m [(ωy z - ωz y) vx + (ωz x - ωx z) vy + (ωx y - ωy x) vz] +
+ ½ m [(ωy z - ωz y)2 + (ωz x - ωx z)2 + (ωx y - ωy x)2]
или
T = T2 + T1 + T0,
где
T2 = ½ m (vx2 + vy2 + vz2),
T1 = m [(ωy z - ωz y) vx + (ωz x - ωx z) vy + (ωx y - ωy x) vz],
T0 = ½ m [(ωy z - ωz y)2 + (ωz x - ωx z)2 + (ωx y - ωy x)2].
Составим уравнения Лагранжа и приведём их к виду (3.6).
Тогда получим:
m ax = X + ∂T0/∂x + 2mωzvy - 2mωyvz,
m ay = Y + ∂T0/∂y - 2mωzvx + 2mωxvz,
m az = Z + ∂T0/∂z + 2mωyvx - 2mωxvy.
В этих уравнениях X, Y, Z – проекции равнодействующей приложенных к точке сил на оси подвижной системы координат x, y, z. Гироскопические силы в данном примере равны
Гx = 0 + 2mωzvy - 2mωyvz,
Гy = -2mωzvx + 0 + 2mωxvz, (1.3.15)
Гz = 2mωyvx - 2mωxvy + 0.
Матрица коэффициентов при скоростях vx, vy и vz, как и следовало ожидать, является кососимметричной:
| 0 2mωz -2mωy |
G = | -2mωz 0 2mωx |.
| 2mωy -2mωx 0 |
Из равенств (3.15) видно, что в данном примере гироскопические силы Гx, Гy, Гz являются проекциями кориолисовой силы инерции Jc = -2mω × vr.
Покажем, что производные ∂T0/∂x, ∂T0/∂y, ∂T0/∂z равны проекциям силы B, численно равной mρω2 (ρ – расстояние от точки М до оси вращения ω) и направленной от оси вращения к точке. Для этого рассмотрим силу B, определяемую равенством
B = ∂T0/∂x i + ∂T0/∂y j + ∂T0/∂z k.
Имеем:
∂T0/∂x = m [(ωz x - ωx z)ωz - (ωxy - ωyx)ωy].
Добавим и вычтем в квадратных скобках ω2x и учтём, что ω·r = ωxx + ωyy + ωzz. Тогда
∂T0/∂x = m [ω2x - (ω·r) ωx].
Аналогично
∂T0/∂y = m [ω2y - (ω·r) ωy],
∂T0/∂z = m [ω2z - (ω·r) ωz].
Умножим первое равенство на i, второе на j, а третье на k и сложим. Тогда получим: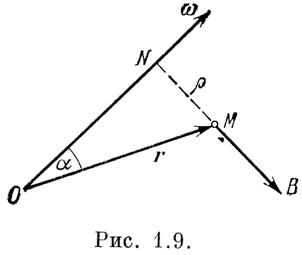
B = m [ω2r - (ω·r)·ω],
или, вынося ω2 за скобки,
B = mω2[r - (ω0·r)·ω0],
где ω0 = ω/ω – орт вектора угловой скорости ω.
Обращаясь к рис. 1.9, мы видим, что
ω0·r = 1·r·cos α = ON, (ω0·r)·ω0 = ON,
r - (ω0·r)·ω0 = NM = ρ и, следовательно, сила B равна
B = mω2NM = mω2ρ, | B | = mω2ρ.
Таким образом, в данном примере сила B, имеющая проекции ∂T0/∂x, ∂T0/∂y и ∂T0/∂z, равна по величине и направлению центробежной силе. Этим объясняется термин "обобщённые центробежные силы" для Bk = ∂T0/∂qk – см. равенство (3.8).»
Меркин Д. Р., Гироскопические системы, "Наука", 1974, ст. 52-54.
Обратите внимание, что в такой постановке задачи инерционная центробежная сила равная
B = m·ω2·ρ может совершать работу. Гироскопическими свойствами обладает только сила Кориолиса Jc = -2·m·ω×vr. Хорошей моделью для рассмотрения этого движения является центрифуга.
Получается следующая структура сил инерции:
1. Центробежная сила равна B = m·ω2·ρ, где ω – угловая скорость вращения системы отсчёта в которой рассматривается движение; ρ – радиус-вектор, соединяющий материальную точку и ось вращения. Радиус-вектор ρ перпендикулярен угловой скорости (оси).
2. Сила Кориолиса равна Jc = -2m·[ω × vr], где vr – скорость движения тела относительно вращающейся системы отсчёта.
3. Ньютоновские силы взаимодействия по третьему закону обозначим через F.
В сумме это будет выглядеть так
m·ar= F + B + Jc = F + m·ω2·ρ - 2m·[ω × vr], где ar – ускорение во вращающейся системе.
Если рассматривать движение только в плоскости, то
[ω × ve] = [ω×[ω × ρ]] = ω·(ω·ρ) - ρ·(ω·ω) = - ω2·ρ, где ve – скорость вращения относительно оси, т. е. переносная скорость точки, согласно теореме Эйлера, тогда
m·ar = F - m·[ω × ve] - 2m·[ω × vr].
m·ar = F - m·[ω × v] - m·[ω × vr], где v = ve + vr – абсолютная скорость в инерциальной системе отсчёта. ...

|

