Выше

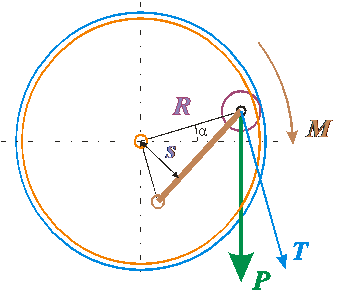
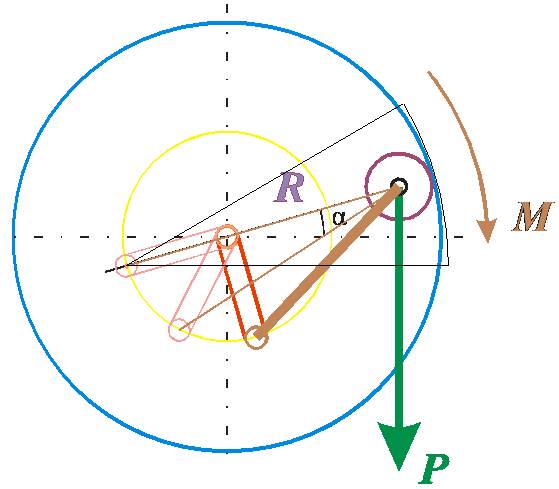
Статья из сайта petrovlam.ru автор Петров В. М. Введена:03.11.11

Михаил, желаю Вам самого Доброго Вечера!
      
       На рисунке 1 повторена схема для вычисления момента вращения.
       Ваши вычисления и мои измерения показали, что величину момента для данной схемы следует находить по формуле

M = R × T

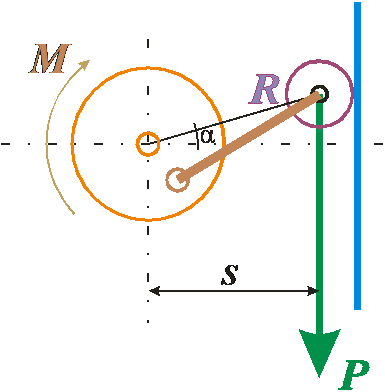
Рис. 1

       На рисунке 2 схема слегка изменена. Теперь вместо обечайки используется плоская стенка (голубой цвет). Всё остальное оставлено без изменения.

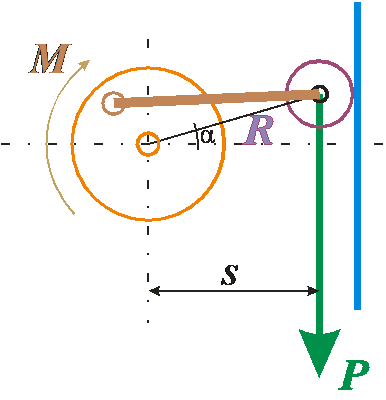
Рис. 2

Вопрос 1:

       Поскольку тангенциальная сила Т отсутствует, постольку можно предположить, что для вычисления момент можно применить формулу:

M = s × P

       При этом положение цапфы, вокруг которой вращается тяга, относительно оси ротора значения не имеет. В частном случае тяга может принимать вид и такой, как показано на рисунке 3. Или любой другой вид.

Рис. 3

Я правильно понимаю?

Мой ответ в письме был такой:

Здравствуйте, Владимир Максимович. Формула M = P·s, правильна. Однако, во всём этом есть особый случай.
На рисунке 3 Вы изобразили, что тяга практически перпендикулярна направляющей и соответственно параллельна горизонтальной оси. С математической точки зрения это особая точка. В этой точке нарушается связь между вертикальным перемещением груза и поворотом ротора. Фактически внешний момент в этом случае уже не может повернуть ролик, так как сила, действующая на него через тягу перпендикулярна направляющей, а ролик не может повернуть ротор, так как он перемещается перпендикулярно тяге. Формула M = P·s будет работать всегда правильно за исключением подобных особых точек и это надо учитывать при её использовании. Главная формула это всегда M = F_R·S, полученная ранее, из неё следует и M = P·s, в результате преобразований. В процессе этих преобразований происходит потеря информации об особых точках и это всегда надо иметь ввиду.
С уважением, Михаил.

Этот ответ требует уточнения.

В формуле M = P·s, появится ещё одно слагаемое.

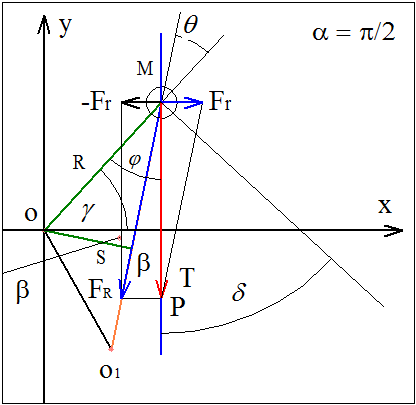
F_R·cos(β) = P;       F_R·sin(β) = F_r;      F_r = P·tg(β);       S = R·cos(β + γ).

M = P·R·cos(γ) - F_r·R·sin(γ) = P·R·cos(γ) - P·R·tg(β)·sin(γ) =

= P·R·cos(γ) - P·R·(sin(β)/cos(β))·sin(γ) =

= P·R·(cos(β)·cos(γ) - sin(β)·sin(γ))/cos(β) = P·R·cos(β + γ)/cos(β).

M = P·R·cos(γ) - F_r·R·sin(γ) = P·s - F_r·R·sin(γ) = P·R·cos(γ) - P·R·tg(β)·sin(γ).

Этот же результат можно получить из более общей расчётной схемы на предыдущей странице.

...

Статья из сайта petrovlam.ru автор Петров В. М. Введена:04.11.11

Михаил, желаю Вам самого Доброго Вечера!
      
А.   На рисунке 3 тяга СЛУЧАЙНО показана практически горизонтальной. Но, как говорится: «нет худа без добра». Эта случайность и мне позволила подумать вот над чем:

Рис. 3

1.    Если считать штангу строго горизонтальной, то будет ли при этом падение груза генерировать момент вращения на роторе?
       Я думаю, что по Вашей формуле – НЕТ! И это – не смотря на то, что наше произведение НЕ будет равным нулю!

       Я правильно мыслю?

ролик не может повернуть ротор, так как он перемещается перпендикулярно тяге. Формула   M = P·s  будет работать всегда правильно за исключением подобных особых точек и это надо учитывать при её использовании.

       Если правильно (в противном случае – упрёмся в нонсенс), то придётся менять методику вычисления величины генерируемого момента. Нельзя допустить, чтобы формула выбиралась в зависимости от того, насколько близко тяга приблизилась к горизонтальности.
       К примеру (как вариант), проекция вектора Р на тягу автоматически приближается к нулю, по мере принятия штангой горизонтальной ориентации. И тогда строго горизонтальная ориентация перестанет считаться какой-то особой позицией. Просто в этой позиции сила действия груза на цапфу АВТОМАТИЧЕСКИ становится равной нулю, не создавая на роторе, по этой причине, ни какого момента вращения!
ПРИМЕЧАНИЕ
       Полезно учесть, горизонтальная ориентация создаётся тягой и в позиции, ниже оси ротора.

2.    Причём здесь вообще какая-то штанга с её особой угловой ориентацией?!
       Ведь в нашей (Вашей) формуле она вообще никак НЕ ЗАДЕЙСТВОВАНА!

3.    Если согласиться с тем, что генерируемый грузом положительный момент вращения направлен ПО часовой стрелке, то уже в следующий (очень короткий) отрезок времени (после горизонтальной ориентации) штанга, попав в область, граничащую с горизонтальностью, начнёт генерировать на роторе положительный момент вращения, хотя бы потому уже, что наклонная тяга начинает передавать цапфе компонент от вектора Р, направленный вдоль тяги. А это самоуправство не предусмотрено Вашей формулой!
       Ведь расстояние s фактически ещё не изменилось.

4.    В следующий отрезок времени груз продолжает падать. Груз уже НЕ контактирует со стенкой, но ещё не долетел до препятствия.
       Что происходит в этой ситуации с генерацией момента вращения?

       Тут решение явно НЕ однозначно.

       С одной стороны - от груза цапфе через тягу передаётся компонента от вектора Р, направленная вдоль тяги и понуждающая ротор к положительному вращению.
       С другой стороны – по правилам теоретической механики действие груза переносится в ось цапфы и тем самым побуждает ротор к отрицательному вращению.
       Одновременно с переносом силы положено к приёмной точке прикладывать и компенсирующий момент. Но в нашем случае эту процедуру можно пропустить, так как тяга свободно вращается по цапфе.
       Никакие другие силы в этом промежутке времени на ротор НЕ ДЕЙСТВУЮТ!
       А как же тогда быть с расстоянием s?
       Вероятнее всего, вместо расстояния s придётся использовать расстояние от оси цапфы до оси ротора?
       Но, опять же, положение цапфы на роторе Вашей формулой игнорируется!

5.    В конечном счёте, тяга упадёт-таки на ось ротора. И что делать в этой ситуации -  вообще лучше оставить на потом.

      Да, Владимир Максимович, рисунок с почти горизонтальной тягой весьма кстати, так как наводит на проблему, которую надо рассмотреть более подробно. Что касается выбираемых формул, то здесь наши возможности весьма ограничены, рядом
M = F_R·S = P/cos(β)·R·cos(β + γ) = P·R·cos(γ) - P·R·tg(β)·sin(γ). Из которого видно, что существует особая точка β = 90° и в этой точке момент по формуле, стремится к бесконечности. Однако это справедливо только для идеального случая, когда конструкция абсолютно жесткая. На практике момент определяется внешним сопротивлением на роторе и поэтому совсем не обязан, стремится к бесконечности. В особой точке происходит разрыв механической связи, и величины входящие в формулу могут принимать любые значения. На практике эти значения зависят от трения и возможных деформаций конструкции. В любом случае необходимо изучить наблюдаемые особенности и если есть возможность исключить их соответствующим выбором параметров конструкции.
      Особые точки появляются не только в случае неопределенности механической связи, они могут возникать и в точках, где возможно заклинивание. Например, формулу момента для окружной направляющей M = T·R можно преобразовать так
M = T·R = F_R·S = T/cos(γ + β)·R·cos(γ + β), так как F_R·cos(γ + β) = T; R·cos(γ + β) = S. В этом случае для силы F_R существует особая точка
F_R = T/cos(γ + β), при γ + β = 90° сила F_R стремится к бесконечности и на практике в районе этой точки произойдёт заклинивание механизма. Эта особая точка исключается правильным выбором параметров механической конструкции. ...

13.11.2011 г.

      
       С математическими выкладками спорить – НЕ эффективно!
       Но и со здравым смыслом спорить – тоже малополезно!
       Я понимаю, что здравый смысл – не всегда прав. Но я также понимаю и то, что лобовое использование математического аппарата тоже не всегда даёт правильный результат. И этому есть примеры.
       Значит, где-то имеется середина!

       Я чуть-чуть изменил схему. Теперь ротор отсутствует. Он превратился в шатун.

       С точки зрения математика – ничего НЕ изменилось. Я прав?

       Хотя теперь очень даже видно, что мгновенному моменту вращения будет не всё равно, с какой позиции шатун начинает своё движение. И это – при том, что, и начальное положение груза в пространстве относительно оси шатуна, и его начальная масса остались прежними.

Да, Владимир Максимович, математика останется прежней. Формула M = T·R, будет выражать идеальную ситуацию, строго справедливую только при отсутствии трения и деформаций. На опыте мы убедились, что она справедлива с достаточной технической точностью 12% в диапазоне 0 – 60°, при определённом, выбранном Вами, положении тяги. Формула M = T·R это выражение через математику свойств выбранной нами расчётной модели. Эту модель можно усложнить, введя в неё трение и деформацию и соответственно получить значительно более сложную формулу. Однако, стоит ли это делать, когда мы и так имеем достаточно полную картину о возможных особенностях рассматриваемой схемы. Единственная особая точка (для окружной направляющей) появляется, когда тяга строго проходит через радиус. На практике из-за трения это уже будет не точка, а целая угловая зона в районе радиуса (на рис.). В этой зоне давление тяги на окружную направляющую может значительно увеличивать величину трения и деформации, что может привести к заклиниванию механизма. Величина этой зоны существенно неопределённа, так как зависит от многих механических факторов, которые трудно учесть. Задача заключается не в поиске новых формул, которые описывают эту ситуацию лучше, а в правильном применении формулы M = T·R для окружной направляющей, с учётом известных особенностей. Формула M = T·R, появляется не как результат лобового применения математики, а в большей степени как результат выбора расчётной модели. Эта расчётная модель должна соответствовать механике Ньютона, и этим выбор модели сильно ограничен. На опыте Вы убедились, что расчётная модель построенная на основе "физических процессов" не соответствует опыту. ...

С уважением Михаил. 19.11.2011 г.

О вечном реактивном двигателе.

    В интернете можно встретить следующие, подобные этим рассуждения. Если ракета движется со скоростью превышающей скорость истечения рабочего тела, то можно добиться того, что генерируемая реактивным двигателем полезная механическая мощность, будет больше, чем мощность, расходуемая на выброс рабочего тела, а значит привод со сверх–единичным коэффициентом полезного действия на этом принципе, возможен.
    Действительно, если ракета движется со скоростью рабочего тела относительно выбранной инерциальной системы отсчёта, то рабочее тело после истечения будет покоиться относительно этой системы отсчёта, т. е. формально, если не учитывать потери на преобразование энергии топлива в механическую энергию, вся внутренняя энергия топлива пойдёт на увеличение скорости ракеты. Кажется, что достаточно разогнать ракету выше скорости истечения рабочего тела и работа будет уже больше затрат энергии на разгон рабочего тела.
    Чтобы понять, почему эта идея несостоятельна, решим следующую простую задачу.

    Пусть относительно оси на радиусе R покоится реактивный двигатель, рабочим телом которого является шар. Энергия для ускорения шара сосредоточена в пружине, которая взводится внешним источником энергии.
В начале цикла двигатель разгоняется внешним источником энергии до скорости, превышающей скорость выброса шара. Шар выбрасывается, и его энергия после падения полностью аккумулируется внешним источником энергии. Потом двигатель тормозится до нулевой скорости тоже с сохранением его энергии во внешнем аккумуляторе, пружина взводится, и шар снова устанавливается на рабочее место. Далее этот цикл повторяется.
Исследуем баланс энергии этого цикла.

Начальная энергия системы E₀, складывается из потенциальной энергии пружины E_п и энергии, необходимой на разгон
двигателя E_р.
E₀ = E_п + E_р.

Найдём связь между приращениями скорости шара v_ш и двигателя v_д после распрямления пружины. Пусть масса шара m, а масса двигателя M. Пружина и все другие элементы системы для упрощения задачи не имеют массы. Приращение скоростей шара и двигателя при поступательном движении подчиняется закону сохранения импульса и не зависит от относительной скорости движения системы шар—двигатель (это доказано опытом). Будем считать, что срабатывание пружины происходит почти мгновенно, т. е. рассматриваемый участок траектории можно считать практически прямым, это нужно только для упрощения математики задачи.
m·v_ш + M·v_д = 0.

Энергия системы шар+пружина+двигатель всегда сохраняется относительно их общего центра масс (это доказано опытом). Фактически это внутренняя энергия системы шар+пружина+двигатель.
m·v_ш²/2 + M·v_д²/2 = E_п (после срабатывания пружины).

Найдём скорость системы шар+двигатель после разгона.
E_р = (m + M)·v²/2, это фактически внешняя энергия системы шар+двигатель относительно принятой системы отсчёта.

v = √(2·E_р/(m + M)).

Найдём скорость шара и двигателя после разгона и распрямления пружины.
v_ш1 = v + v_ш;     v_д1 = v + v_д.

Найдём полную энергию системы после разгона и срабатывания пружины.
m·v_ш1²/2 + M·v_д1²/2 = m·(v + v_ш)²/2 + M·(v + v_д)²/2 =

= m·v²/2 + m·v_ш²/2 + m·v·v_ш+ M·v²/2 + M·v_д²/2 + M·v·v_д= (1)

= (m + M)·v²/2 + m·v_ш²/2 + m·v·v_ш+ M·v_д²/2 + M·v·v_д=

= (m + M)·v²/2 + m·v_ш²/2 + M·v_д²/2 + v·(m·v_ш + M·v_д) =

= (m + M)·v²/2 + E_п + v·(m·v_ш + M·v_д) =, так как m·v_ш²/2 + M·v_д²/2 = E_п.

= (m + M)·v²/2 + E_п =, так как m·v_ш + M·v_д = 0.

= E_р + E_п = E₀, так как E_р = (m + M)·v²/2. Таким образом, полная энергия системы после разгона и срабатывания пружины равна начальной энергии системы, т. е. даровой работы нет и не может быть.

Обратите внимание на энергетическую сумму со смешанными скоростями (m·v·v_ш+ M·v·v_д) в выражении (1). Относительно инерциальных систем отсчёта эта сумма всегда равна нулю. В неинерциальных системах отсчёта, например в центрифуге, эта сумма не равна нулю. В этом случае её физический смысл связан с наличием энергии "поля", т. е. искусственной гравитации в центрифуге. Эта энергия всегда потенциальна и не может быть использована для совершения работы на замкнутой траектории, т. е. предположение, что m·v_ш + M·v_д ≠ 0, тоже не позволяет совершать даровую работу. В этом случае просто усложняется задача в силу наличия не инерциальной системы отсчёта.

Михаил Ost 11.12.2011 г.

Работа центробежной силы.

Рассмотрим вращающуюся центрифугу на радиусе R. Пусть ΔR – приращение радиуса R; ω = const – угловая скорость вращения центрифуги; v = ω·R – абсолютная скорость вращения на радиусе R; Δv = ω·ΔR – приращение скорости при изменении радиуса; m – масса тела. Для выполнения условия постоянства угловой скорости будем считать, что момент инерции центрифуги очень большой.
Найдём приращение кинетической энергии тела при перемещении по радиусу центрифуги.

ΔE = m·(v + Δv)²/2 - m·v²/2 = m·v²/2 + m·Δv²/2 + m·v·Δv - m·v²/2 = m·Δv²/2 + m·v·Δv.
Приращение кинетической энергии определяется двумя слагаемыми разного дифференциального порядка. Второе энергетическое слагаемое смешанное, состоит из скорости и приращения скорости. Оно и определяет изменение энергии. Если считать, что центробежное ускорение подобно силе гравитации, то работу, связанную с перемещением тела на приращении ΔR можно записать так
A = m·g·ΔR.

Пусть A = ΔE, т. е. считаем, что работа при движении тела вдоль радиуса, совершается за счёт изменения окружной кинетической энергии тела.
m·g·ΔR = m·Δv²/2 + m·v·Δv = m·ω²·ΔR²/2 + m·ω²·R·ΔR;

g = ω²·ΔR/2 + ω²·R. При ΔR → 0 имеем, g = ω²·R = ω·v.
Мы получили правильное выражение для центробежного ускорения. Работа центробежной силой, совершается за счёт изменения окружной кинетической энергии и поэтому даровой работы от центробежной силы не бывает. Обратите внимание, что для изменения энергии ΔE, при движении тела вдоль радиуса, требуется действие окружной силы. Это действует сила Кориолиса. Найдём эту силу. Момент импульса тела равен
L = J·ω, где J = m·R² – момент инерции тела.

Момент силы действующий на тело, можно найти как производную по времени от момента импульса
M = dL/dt = d(m·R²·ω)/dt = -2·m·R·v_r·ω, где v_r – скорость движения тела вдоль радиуса.

Находим силу Кориолиса
F = M/R = -2·m·v_r·ω.
Сила Кориолиса появляется в результате изменения момента инерции тела при движении вдоль радиуса центрифуги при ω = const. Обратите внимание, что сила Кориолиса появляется всегда, когда центробежная сила совершает работу, т. е. есть движение вдоль радиуса. Между центрифугой и телом, действует момент сил, который обеспечивает соблюдение закона сохранения момента импульса.

Отменим условие ω = const, тогда
M = dL/dt = d(m·R²·ω)/dt = d(m·R·v)/dt = -m·v_r·v + m·R·a = -m·ω·R·v_r + m·R·a, где a – окружное ускорение тела.

Окружная сила равна
F = M/R = -m·ω·v_r + m·a = m·(-ω·v_r + a).
Если момент инерции центрифуги равен нулю, то a = 0 и F = -m·ω·v_r, т. е. удвоения при окружной компоненте силы Кориолиса уже нет. Эти вычисления справедливы, если в качестве угловой скорости, используется угловая скорость тела. В этом случае радиальная компонента силы Кориолиса равна нулю.
Возникает вопрос, почему a = 0, если момент инерции центрифуги равен нулю. Рассмотрим гипотетический случай, когда центробежная сила работы не совершает. Пусть тело на стержне, вращается вокруг центра. Будем изменять радиус вращения тела. В этом случае, при отсутствии работы центробежной силы, не будет изменения абсолютной скорости тела, т. е. не будет касательного ускорения. Фактически мы предполагаем, что за работу центробежной силы в выражении
F = m·(-ω·v_r + a), отвечает слагаемое -ω·v_r, а за окружное ускорение, связанное с действием других тел "a". В случае центрифуги ускорение "a", возникает из-за радиального градиента скоростей, который при a = 0 отсутствует, так как нет момента со стороны центрифуги. При ω = const, имеем a = -ω·v_r, поэтому и получается удвоение в силе Кориолиса. В выражении F = m·(-ω·v_r + a) ускорения разделены по физическим свойствам, т. е. "а", отвечает за движение через градиент скорости, а -ω·v_r, связано с работой центробежной силы. Без -ω·v_r невозможно выполнение закона сохранения энергии при совершении работы центробежной силой.
    Удвоение в формуле силы Кориолиса это только частный случай интерпретации силовых взаимодействий в центрифуге при ω = const. Условие ω = const, связано с выбором неинерциальной системы отсчёта, обладающей достаточным моментом инерции, чтобы можно было считать угловую скорость вращения, независящей от механических процессов протекающих в ней. Например, в качестве такой неинерциальной системы отсчёта может служить вращающаяся планета.
    В неинерциальной системе отсчёта, кроме сил обусловленных взаимодействием по третьему и второму закону Ньютона, на тело действуют инерционные силы, Кориолиса и центробежная. Центробежная сила всегда работает только в комплексе с силой Кориолиса. Если в неинерциальной системе отсчёта тело движется без участия Ньютоновских сил по кривой траектории, то попытка изменить (спрямить) эту траекторию, приводит к появлению комплекса инерционных сил. Поэтому без силовое криволинейное движение в неинерциальных системах отсчёта можно считать движением по инерции или гироскопическим. ...

Михаил Ost 17.12.2011 г.

Истечение жидкости из отверстия вращающейся центрифуги.

Найдем потенциальную энергию одного кубического метра жидкости, находящейся в центрифуге под действием искусственной гравитации центробежной силы g = ω²·R
$ \displaystyle P = ρ \int ω^2 \cdot R \cdot dR = ρ \cdot ω^2 \int R \cdot dR = ½ \cdot ρ \cdot ω^2 ·R^2 = ½ \cdot ρ \cdot v^2 $, где ρ – плотность жидкости.

Потенциальная энергия P равна кинетической энергии слоя жидкости на радиусе R.
Максимальная энергия истекающей жидкости будет равна разности потенциалов между поверхностью и дном
½·ρ·v_ист² = ½·ρ·v_дно² - ½·ρ·v_пов².

Из этого выражения видно, что кинетическая энергия истечения жидкости формируется из кинетической энергии вращающейся центрифуги, наполненной жидкостью, и поэтому даровой энергии при истечении нет.

Эту формулу можно записать по другому
½·ρ·v_ист² = ½·ρ·v_дно² - ½·ρ·v_пов² = ½·ρ·ω²·R_дно² - ½·ρ·ω²·R_пов² = ½·ρ·ω²·(R_дно² - R_пов²) =

= ½·ρ·ω²·(R_пов+ R_дно)·(R_дно- R_пов) = ρ·ω²·R_ср·ΔR, где (R_пов+ R_дно)/2 = R_ср;     R_дно- R_пов = ΔR.

Пусть g_ср = ω²·R_ср, тогда

½·ρ·v_ист² = ρ·g_ср·ΔR.

v_ист = √(2g_ср·ΔR). Эту формулу, часто называют формулой Торичелли, она показывает, что скорость истечения идеальной жидкости не зависит от физических свойств жидкости и определяется только высотой столба ΔR и ускорением свободного падения.

    В действительности скорость истечения жидкости будет зависеть, от геометрических характеристик отверстия, его расположения на стенке, числа Re. Поэтому в формулу Торичелли обычно вводится поправка, называемая коэффициентом скорости φ. При учёте указанной поправки скорость истечения будет
v_ист = φ·√(2g_ср·ΔR).

    Величина φ в общем виде как функция числа Рейнольдса может быть представлена φ = φ(Re). Её величина изменяется в пределах 0,94–0,99. Таблицы значений φ можно найти в гидравлических справочниках.

Обратите внимание, что в этом варианте задача решается без учёта сил Кориолиса, и поэтому это решение является не строгим и применимо только при ΔR << R, т. е. когда "поле" центробежной силы можно считать однородным. При наличии градиентов в "поле" центробежной силы, движение жидкости усложняется. ...

Михаил Ost 18.12.2011 г.

О реактивном движении.

Комментарии к сообщению Виктора–V111 на сайте petrovlam.ru.

«... Т.к. выброс массы рабочего тела будет происходить в течении периода времени, это значит, что первая часть массы воды уже вылетевшая из сопла передаст часть своей кинетической энергии остатку массы рабочего тела (воды) в маховике, которая ещё не успела выйти из сопла!!!

Это значит, что остаток массы воды в маховике получил дополнительное увеличение кинетической энергии выраженной в виде роста остаточной скорости массы воды в маховике без дополнительных затрат энергии на ускорение маховика!!!

Именно этот процесс частичного обратного возвращения кинетической энергии без дополнительных затрат энергии приводит не к экономии затрат энергии а к неограниченному росту КПД реактивной системы!

Указанный рост КПД системы ограничен в данном случае не обычными вами любимыми 100%, а запасом воды в маховике, это значит, что при достаточном запасе воды в маховике при заданной скорости сброса воды, КПД системы легко ПРЕВЫСИТ 100%, ...».

Вычислим дифференциал импульса ракеты
dp_р = d(M + m)·V) = dm·V + (M + m)·dV.

Вычислим дифференциал импульса рабочего тела
dp_т = d(m_т·(v + V)) = dm_т·(v + V) + m_т·d(v + V) = dm_т·(v + V) + m_т·dv + m_т·dV.

Для реального процесса истечения dv = dV = 0, так как израсходованное рабочее тело движется по инерции, и поэтому останется только
dp_т = d(m_т·(v + V)) = dm_т·(v + V).

Запишем уравнение закона сохранения импульса для ракеты в дифференциальном виде. Это уравнение соответствует трём законам Ньютона для любой выбранной инерциальной системы отсчёта, в любой момент времени
dp_р + dp_т = (M + m)·dV + dm·V + dm_т·(v + V) = 0;

(M + m)·dV + dm_т·v = 0; (M + m)·dV - dm·v = 0 (1), где M – масса ракеты; m – оставшаяся масса топлива; dV – дифференциал скорости ракеты; dm – дифференциал оставшейся массы топлива; dm_т – дифференциал истраченной массы топлива; m + m_т = m₀; dm = -dm_т; v – скорость истечения топлива относительно ракеты. Из этого уравнения можно получить закон реактивного движения, разделив уравнение на дифференциал времени dt
(M + m)·(dV/dt) - (dm/dt)·v = 0.

a = (dm/dt)·v/(M + m)     (2.0) – ускорение ракеты в любой момент времени относительно выбранной инерциальной системы отсчёта.

Сила тяги равна
F_р = (M + m)·a = (dm/dt)·v     (2.1).

Найдем из (1) скорость ракеты при условии v = const. Это условие искусственное, так как скорость истечения зависит от ускорения ракеты.
dV = dm/(M + m)·v. Интегрируем по дифференциалу массы на интервале от M + m₀ до M при dm = d(M + m).

V - V₀ = v·∫d(M + m)/(M + m) = v·Ln((M + m₀)/M) = v·Ln(1 + m₀/M) (3), где m₀ – начальная масса рабочего тела; V₀ – начальная скорость ракеты. Это формула Циолковского. Формула была получена интегрированием уравнения, полученного из закона сохранения импульса и поэтому согласованна с законом сохранения энергии. Функцию количества движения можно получить из функции кинетической энергии
dE = d(m·V²/2) = m·V·dV;     dE/dV = m·V – энергия, приходящаяся на единицу скорости.

Уравнения (2.) соответствуют опыту, что подтверждает правильность уравнений (1).

    Запишем дифференциальное уравнение изменения энергии для системы ракета+(масса топлива).
dE = (M + m)·V·dV + dm·V²/2 - dm·(v + V)²/2 =     (4)

= (M + m)·V·dV + dm·V²/2 - dm·v²/2 - dm·V²/2 - dm·v·V =

= (M + m)·V·dV - dm·v²/2 - dm·v·V =

= {(M + m)·V·dV - dm·v·V} - dm·v²/2 =

= V·{(M + m)·dV - dm·v} - dm·v²/2 = -dm·v²/2 = dm_т·v²/2 (5), так как (M + m)·dV - dm·v = 0.

Таким образом, энергия системы ракета+(масса топлива) всегда меняется на величину энергии затраченной на разгон рабочего тела при скорости истечения не зависимо от текущей скорости ракеты. Соответственно, если энергия рабочего тела была получена за счёт внешней энергии, то при использовании ракеты в качестве двигателя, даровой внешней энергии получить нельзя.

Проинтегрируем уравнение dE = dm_т·v²/2 на участке разгона при скорости истечения v = const
E_т = m₀·v²/2.

Найдем энергию ракеты в конце разгона E_р = M·v²·Ln²((M + m₀)/M)/2.

Найдём коэффициент полезного действия при разгоне массы ракеты M

К.П.Д = E_р/(E_р + E_т) = E_р/E₀ = M·v²·Ln²((M + m₀)/M)/2/(m₀·v²/2 + M·v²·Ln²((M + m₀)/M)/2) =, где E₀ – полная механическая энергия топлива.

= 1/(1 + m₀·v²/2/(M·v²·Ln²((M + m₀)/M)/2)) = 1/(1 + (m₀/M)/Ln²(1 + m₀/M)) < 1.

Механический коэффициент полезного действия всегда меньше единицы. Он не зависит от свойств рабочего тела.
Например, пусть m₀/M = 10, тогда К.П.Д = 0,365;
Пусть m₀/M = 100, тогда К.П.Д = 0,175.

Пояснения к уравнению (4)
d((M + m)·V²/2) = (M + m)·V·dV + d(M + m)·V²/2 = (M + m)·V·dV + dm·V²/2 – дифференциал кинетической энергии ракета+топливо.

d(m_т·(v + V)²/2) = m_т·(v + V)·dV + dm_т·(v + V)²/2 = m_т·(v + V)·dV - dm·(v + V)²/2 – дифференциал кинетической энергии истраченной массы топлива.
Обратите внимание, что в уравнении (4) использована только часть этого дифференциала. Причина этого в том, что часть m_т·(v + V)·dV в этой задаче не имеет физического смысла, так как относится к израсходованному топливу, которое уже не связано с ракетой и для него можно считать dV = 0, так как истраченное рабочее тело движется независимо от ракеты по инерции.
Из d((M + m)·V²/2) + d(m_т·(v + V)²/2) при m_т·(v + V)·dV = 0, следует dE = (M + m)·V·dV + dm·V²/2 - dm·(v + V)²/2.

...

Михаил Ost 03.01.2012 г.

Задача о поплавке.

Рассмотрим следующую задачу. В бассейн глубиной 90 метров, с горячей водой 80°С, компрессором на самое дно, подаётся сжатый воздух при температуре 20°С. Сжатый воздух проходит через горячую воду, нагревается и надувает гирлянду поплавков переменного объёма. Поплавки всплывают и совершают работу. Производительность компрессора на атмосферном входе Q = 0,167 м³/с; конечное давление – 9 ат; мощность на валу компрессора – 56,5 кВт. Рассчитать полезную работу этой системы.

Работа по изотермическому сжатию газа компрессором равна
A = (m/μ)·R·T·Ln(p/p₀), где m – масса порции газа; μ = 0,029 кг/моль – молярная масса воздуха; R = 8,314 Дж/(моль·K) – газовая постоянная; T – температура процесса; p/p₀ = 10 – отношение давлений в столбе жидкости; p₀ – атмосферное давление; p – давление в глубине жидкости.

Запишем дифференциал работы через дифференциал массы, объёма и найдем мощность
dA = (dm/μ)·R·T·Ln(p/p₀) = (ρ₀·dV/μ)·R·T·Ln(p/p₀), где dm = ρ₀·dV; ρ₀ = 1,2 кг/м³ – плотность воздуха при 20°С; dV – дифференциал объёма порции воздуха. Делим на дифференциал времени.
N = (ρ₀·Q/μ)·R·T·Ln(p/p₀), Q = dV/dt. Вычисляем мощность при T = 293°K, (20°С) и д. р. выбранных параметрах

N_и = 38,761 кВт.

Дополнительно к работе изотермического сжатия надо добавить статическую работу по вытеснению воды из бака
Δp = 9,80665 м/с²·1000 кг/м³·90 м = 882598,5 Па;   p₀ = 101325 Па.
N_в = Δp·p₀/(Δp + p₀)·Q = 15,179 кВт.

Коэффициент полезного действия компрессора равен (15,179 + 38,761)/56,5 = 0,955. Учитывая, что реальный механический коэффициент полезного действия поршневого компрессора около 90%, то очевидно, что возможности компрессора для этого случая явно преувеличены. Однако для теоретического расчёта это подходит. По мимо статической работы по вытеснению воды, дополнительная работа компрессором затрачивается на ускорение воды при вытеснении. Эта работа практически не обратима на поплавках. Обратите внимание, что средняя величина
ρ·Q = dm/dt = const, постоянна в замкнутом цикле машины. При нагревании плотность уменьшается, объёмный расход растёт (условие непрерывного протекания рабочего тела по замкнутому контуру).

Найдём работу поплавка при подъёме на поверхность. Поплавок объёмом V преодолевает разность давлений
Δp = p_дно - p_пов.

ΔA = Δp·V = g·ρ·Δh·V = g·m·Δh.
Работа, совершаемая поплавком при всплывании, равна работе по опусканию груза равного весу вытесненной жидкости на туже высоту.
Движение поплавка, происходит из-за наличия разности давлений на его верхней и нижней гранях.
Докажем дифференциальное уравнение
dA = dp·V.

Пусть разность давлений между нижней и верхней гранями куба равна Δp = g·ρ·Δx, где Δx – длинна ребра куба. Умножим на площадь грани
F = g·ρ·Δx·Δx² – сила Архимеда.

Найдём дифференциал работы
dA = F·dx = g·ρ·Δx·Δx²·dx, так как дифференциал давления равен dp = g·ρ·dx, то имеем

dA = dp·Δx·Δx² = dp·V, что и требовалось доказать.

...

Оглавление

Продолжение

Назад

Главная страница