| |
Выше
Движение центробежного вибратора по законам сил инерции.
Цель этой работы не утверждать, что силы инерции реально существуют в природе, а показать, что с формальной математической точки зрения, в этом нет противоречия.
Существует ряд утверждений, которые следует поправить. Первое традиционное утверждение, определяет, что силы инерции нарушают закон сохранения энергии, так как
не подчиняются третьему закону Ньютона. Однако закон сохранения энергии не выполняется только для поступательных сил инерции, которые могут совершать работу.
Для гироскопических сил это утверждение не верное. Гироскопические силы инерции не совершают работы по определению и при этом являются внешними силами
по отношению к рассматриваемой механической системе. В классическом варианте они фиктивны. В нашем случае, нет. Их действие компенсирует ортогональную к траектории
составляющую реальных сил, обеспечивая движение тела в направлении вектора скорости с тангенциальным ускорением, например, движение тела по эллипсу под действием
центробежной силы инерции и реальной центростремительной силы.
Философия сил инерции пересекается с принципами механики Аристотеля, который утверждал примерно так, что идеальным, без силовым, является небесное движение по кругу,
а другие земные движения по кривым, протекают под действием сил. Рассмотрим простое движение по прямой. Возникает вопрос, как сформулировать на языке математики идею
Аристотеля. Какая силовая функция обеспечивает преобразование кругового движения тела в прямолинейное? На первый взгляд может показаться, что это нечто сложное,
однако это не так. Я не буду здесь формулировать рассуждения, которые приводят к пониманию этого обстоятельства, а сразу запишу результат и приведу числовые примеры
в виде задач, которые лучше слов показывают теоретическое действие сил инерции и насколько это соответствует реальному движению тел.
\(\vec F_А = m \left[\vec v × \vec ω \right]\) назовём это векторное произведение \(-\) «Силой Аристотеля», где \( \vec ω~-\) угловая скорость тела относительно центра инерциальной системы отсчёта;
\(\vec v~-\) поступательная скорость тела относительно ИСО. Сила действует перпендикулярно скорости тела.
Схема действия силы Аристотеля.
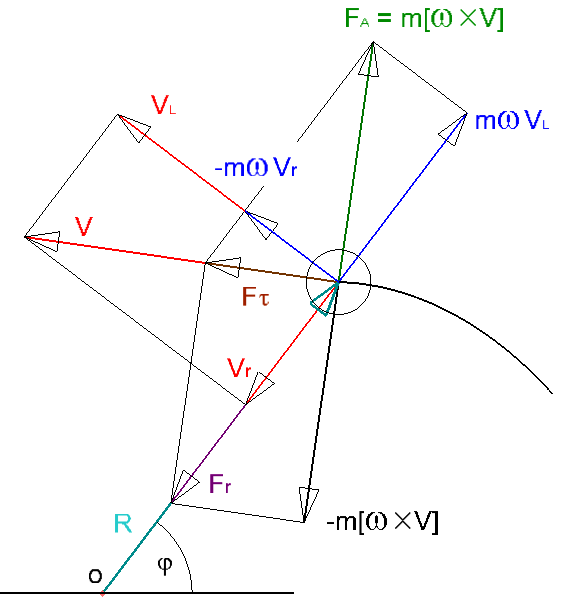
Доказательство гироскопичности этой силы простое \(\vec F_А \cdot \vec v= m \left[\vec ω × \vec v \right] \cdot \vec v= m \left[ \vec v × \vec v \right] \cdot \vec ω =0\). Мощность всегда равна нулю.
При нулевом моменте сил, мощность радиальной силы равна мощности тангенциальной \(F_r \cdot v_r= F_{τ} \cdot v\).
Запишем компоненты этой силы в радиальном и окружном направлении.
\(F_{Аr}= ~~m \cdot ω_z \cdot v_l~-\) радиальная составляющая.
\(F_{Аl}= -m \cdot ω_z \cdot v_r~-\) окружная составляющая.
Угловая скорость \(\displaystyle ω_z = \frac{d \varphi }{dt}\), где \(\varphi ~-\) угол поворота тела относительно оси \(x\) (против часовой стрелки +).
Первая задача о прямолинейном равномерном движении тела под действием силы Аристотеля или движение тела по инерции в классическом понимании.
Используем возможности Mathcad'a.
Составляем блок решения.


Обратите внимание, что это чисто кинематическое решение, так как масса сокращается в уравнении. Сила Аристотеля действует объёмно, как сила гравитации.
Поясним устройство блока решения.
Слева записаны дифференциальные уравнения, справа начальные условия к ним в момент времени 0.
Угловая скорость, очевидно равна \(\displaystyle ω_z = \frac{d \varphi }{dt}\).
Скорость радиальная \(\displaystyle v_r= \frac{dR}{dt}\).
Скорость окружная \(v_l= ω_z \cdot R\).
Далее составляющие ускорения вызванные силой Аристотеля.
\(a_r= ~~ω_z \cdot v_l\).
\(a_l= -ω_z \cdot v_r\).
Последней стоит функция решения, в которой перечислены все функции участвующие в вычислении, её параметры время расчёта движения и число контрольных точек.
В заданных параметрах получим следующие результаты.
Траектория движения тела, есть прямая линия.
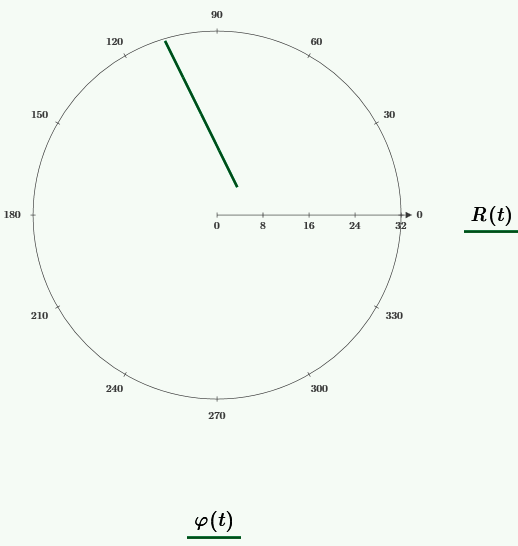
Закон сохранения энергии выполняется.
Найдем разность между начальной энергией и текущей и отобразим на графике. Уровень оценки изменения энергии \(0.01~Дж/кг\).
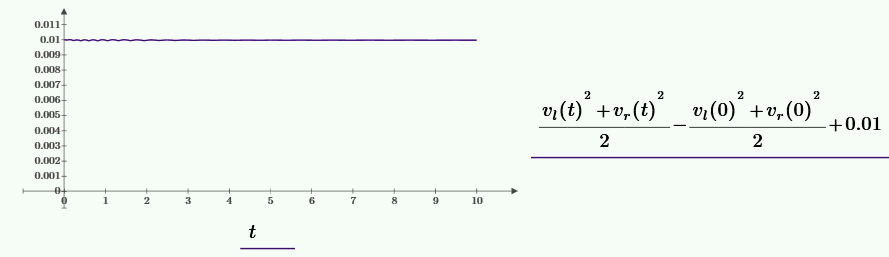
Относительная среднеквадратичная ошибка на интервале \(0-10~сек\) равна \(7.67 \cdot 10^{-4}\)%.
Закон сохранения импульса выполняется, так как модуль скорости не меняется и тело движется по прямой.
Закон сохранения момента импульса выполняется.
Найдём разность между начальным моментом импульса и текущим и отобразим на графике. Уровень оценки изменения момента импульса \(0.02~м^2/c\).
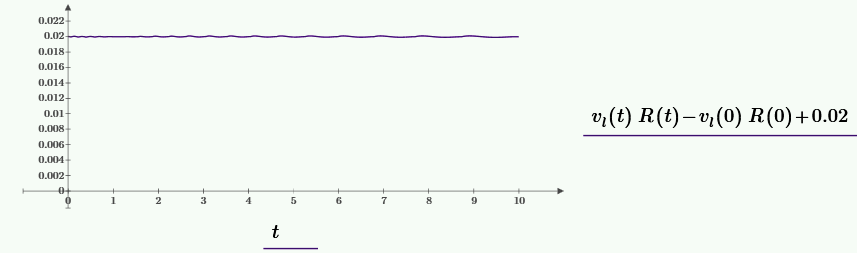
Относительная среднеквадратичная ошибка на интервале \(0-10~сек\) равна \(7.08 \cdot 10^{-4}\)%.
Таким образом мы подтвердили, что сила Аристотеля правильно формирует траекторию движение тела и результат её действия не противоречит законам сохранения.
Угловая скорость.
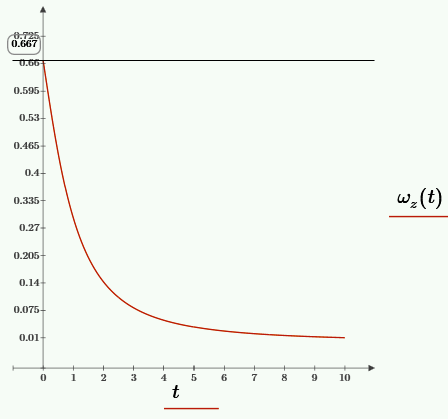
Вторая задача на орбитальное движение двух тел в гравитационном поле.
Блок решения.

Задача решается в условных числах.
\(G=1\).
\(r=1~-\) исходное расстояние между телами.
\(M_1=5; ~~M_2=20; ~~M=M_1+M_2=25\).
\(ω_0 =2~-\) начальная угловая скорость.
Начальные скорости выбраны из условия покоя центра масс системы.
Траектория движения тел эллиптическая. Красной точкой помечен фокус. В фокусе центр масс системы тел.
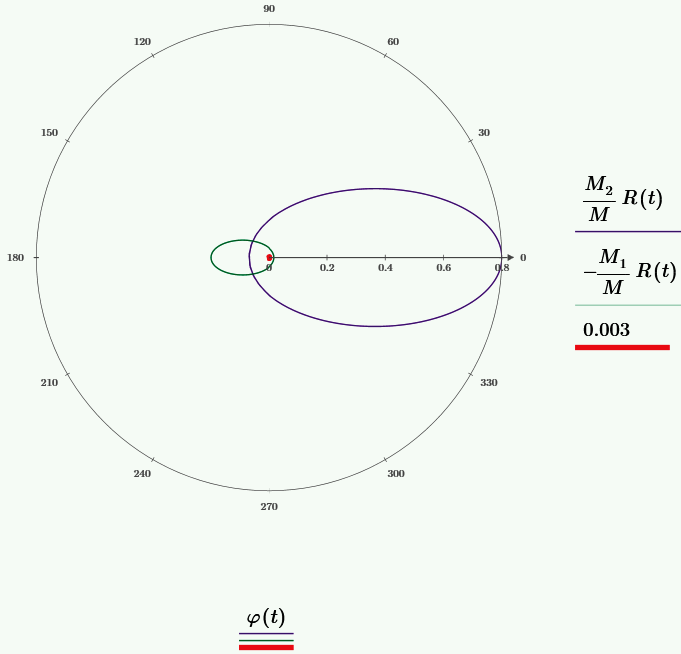
Энергия системы равна
\(\displaystyle E= M_1 \left(\frac{v_{r1}^2 + v_{l1}^2}{2} \right) + M_2 \left(\frac{v_{r2}^2 + v_{l2}^2}{2} \right)- G \cdot \frac{M_1 \cdot M_2}{R}\).
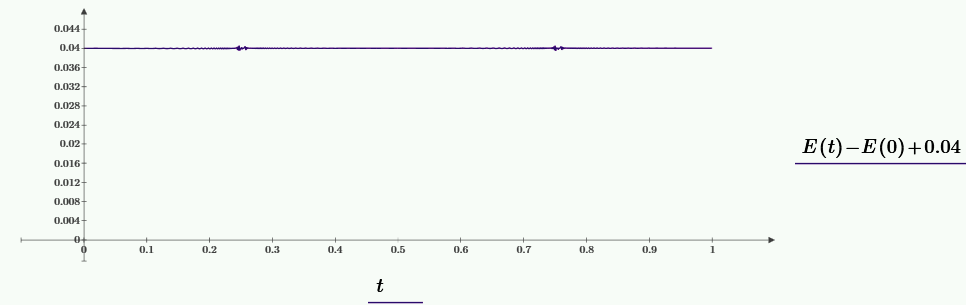
Относительная среднеквадратичная ошибка на интервале \(0-1\) равна \(1.47 \cdot 10^{-4}\)%.
...
Закон сохранения момента импульса.
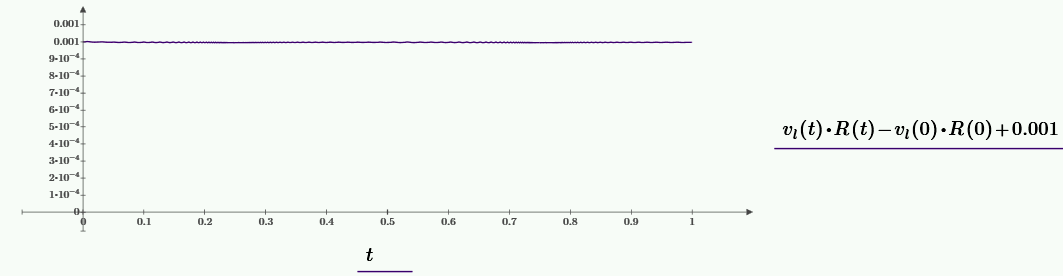
Относительная среднеквадратичная ошибка на интервале \(0-1\) равна \(1.64 \cdot 10^{-4}\)%.
...
Третья задача. Маятник с двумя степенями свободы.
\(\displaystyle \vec a = -ω_0^2 \vec R - \left[\vec ω_z × \vec v \right]\).
Блок решения.
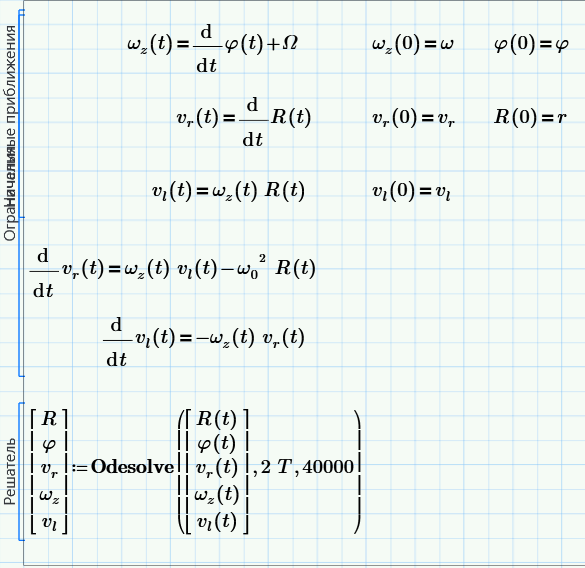
Высота подвеса \(10~м\).
Начальная окружная скорость \(v_l=0.4~м/с\). Начальная радиальная скорость \(v_r=0\).
...
Четвёртая задача. Маятник Фуко.
Блок решения из предыдущей задачи.
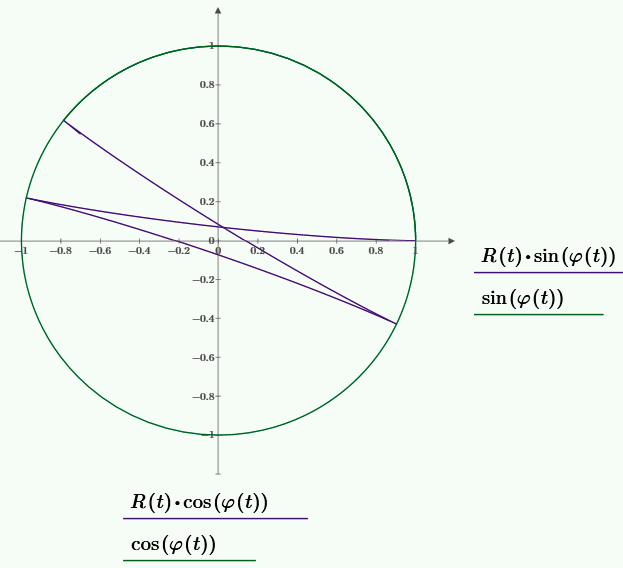
...
Пятая задача, движение тела на пружине.
Блок решения.
...
Предельный случай, вращение тела по кругу. На тело действует центробежная сила.
Шестая задача, движение центробежного вибратора.
Блок решения.
...

Оглавление
|
|

